part 3. Find the value of the trig function indicated, use Pythagorean theorem to find the third side if you need it.

Answers
Answer: \(\bold{9)\ \sin \theta=\dfrac{1}{3}\qquad 10)\ \sin \theta = \dfrac{4}{5}\qquad 11)\ \cos \theta = \dfrac{\sqrt{11}}{6}\qquad 12)\ \tan \theta = \dfrac{17\sqrt2}{26}}\)
Step-by-step explanation:
Pythagorean Theorem is: a² + b² = c² , where "c" is the hypotenuse
\(9)\ \sin \theta=\dfrac{\text{side opposite of}\ \theta}{\text{hypotenuse of triangle}}=\dfrac{4}{12}\quad \rightarrow \large\boxed{\dfrac{1}{3}}\)
Note: 4² + (8√2)² = hypotenuse² → hypotenuse = 12
\(10)\ \sin \theta=\dfrac{\text{side opposite of}\ \theta}{\text{hypotenuse of triangle}}=\dfrac{16}{20}\quad \rightarrow \large\boxed{\dfrac{4}{5}}\)
Note: 12² + opposite² = 20² → opposite = 16
\(11)\ \cos \theta=\dfrac{\text{side adjacent to}\ \theta}{\text{hypotenuse of triangle}}=\dfrac{\sqrt{11}}{6}\quad =\large\boxed{\dfrac{\sqrt{11}}{6}}\)
Note: adjacent² + 5² = 6² → adjacent = √11
\(12)\ \tan \theta=\dfrac{\text{side opposite of}\ \theta}{\text{side adjacent to}\ \theta}=\dfrac{17}{13\sqrt2}\quad =\large\boxed{\dfrac{17\sqrt2}{26}}\)
Note: adjacent² + 7² = (13√2)² → adjacent = 17
Related Questions
What are the additive and multiplicative inverses of h(x) = x â€"" 24? additive inverse: j(x) = x 24; multiplicative inverse: k(x) = startfraction 1 over x minus 24 endfraction additive inverse: j(x) = startfraction 1 over x minus 24 endfraction; multiplicative inverse: k(x) = â€""x 24 additive inverse: j(x) = â€""x 24; multiplicative inverse: k(x) = startfraction 1 over x minus 24 endfraction additive inverse: j(x) = â€""x 24; multiplicative inverse: k(x) = x 24
Answers
The additive inverse of a function f(x) is the function that, when added to f(x), equals 0. In other words, the additive inverse of f(x) is the function that "undoes" the effect of f(x).
The multiplicative inverse of a function f(x) is the function that, when multiplied by f(x), equals 1. In other words, the multiplicative inverse of f(x) is the function that "undoes" the effect of f(x) being multiplied by itself.
For the function h(x) = x - 24, the additive inverse is j(x) = -x + 24. This is because when j(x) is added to h(x), the result is 0:
\(h(x) + j(x) = x - 24 + (-x + 24) = 0\)
The multiplicative inverse of h(x) is k(x) = 1/(x - 24). This is because when k(x) is multiplied by h(x), the result is 1:
\(h(x) * k(x) = (x - 24) * 1/(x - 24) = 1\)
Therefore, the additive inverse of \(h(x) = x - 24\) is \(j(x) = -x + 24\\\),
and the multiplicative inverse of \(h(x) = x - 24\)is \(k(x) = \frac{1}{x - 24}\).
Learn more about additive inverse here:
brainly.com/question/30098463
#SPJ11
Lin notices that the number of cups of red paint is always 2/5 of the total number of cups. She writes the equation r = 2/5 to describe the relationship.
Answers
In the given equation r = 2/5 t "r" is the dependent variable.
Dependent variables:In mathematics, a variable is a symbol that represents a quantity that can take on different values. In many cases, variables can be divided into two types: dependent variables and independent variables.
An independent variable is a variable that can be changed freely, and its value is not dependent on any other variable in the equation.
A dependent variable is a variable whose value depends on the value of one or more other variables in the equation
Here we have
Lin notices that the number of cups of red paint is always 2/5 of the total number of cups.
She writes the equation r = 2/5 t to describe the relationship.
In the equation, r = 2/5 t, "t" represents the total number of cups, while "r" represents the number of cups of red paint.
Here "t" is the independent variable because it represents the total number of cups, which can be changed arbitrarily.
The value of "r" depends on the value of "t" because the number of cups of red paint is always 2/5 of the total number of cups.
Therefore,
In the given equation r = 2/5 t "r" is the dependent variable.
Learn more about Variables at
https://brainly.com/question/1479694
#SPJ1
Complete Question:
Lin notices that the number of cups of red paint is always 2/5 of the total number of cups. She writes the equation r = 2/5 t to describe the relationship. Which is the independent variable? Which is the dependent variable? Explain how you know.
three bolts and three nuts are in a box. two parts are chosen at random. find the probability that one is a bolt and one is a nut.
Answers
The probability of picking one bolt and one nut is 1/2 or 50%.
To find the probability that one is a bolt and one is a nut, we need to use the formula for calculating the probability of two independent events happening together: P(A and B) = P(A) × P(B)
Let's first calculate the probability of picking a bolt from the box:
P(bolt) = number of bolts / total number of parts = 3/6 = 1/2
Now, let's calculate the probability of picking a nut from the box:
P(nut) = number of nuts / total number of parts = 3/6 = 1/2
Since the events are independent, the probability of picking a bolt and a nut in any order is:
P(bolt and nut) = P(bolt) × P(nut) + P(nut) × P(bolt)
P(bolt and nut) = (1/2) × (1/2) + (1/2) × (1/2)
P(bolt and nut) = 1/2
Therefore, the probability of picking one bolt and one nut is 1/2 or 50%.
Learn more about probability
https://brainly.com/question/30034780
#SPJ4
the probability that one chosen part is a bolt and the other chosen part is a nut is 1, or 100%. This makes sense because if we choose two parts at random, we must get one bolt and one nut since there are three of each in the box.
To find the probability that one chosen part is a bolt and the other chosen part is a nut, we need to use the formula for probability:
Probability = (number of desired outcomes) / (total number of outcomes)
There are two ways we could choose one bolt and one nut: we could choose a bolt first and a nut second, or we could choose a nut first and a bolt second. Each of these choices corresponds to one desired outcome.
To find the number of ways to choose a bolt first and a nut second, we multiply the number of bolts (3) by the number of nuts (3), since there are 3 possible bolts and 3 possible nuts to choose from. This gives us 3 x 3 = 9 total outcomes.
Similarly, there are 3 x 3 = 9 total outcomes if we choose a nut first and a bolt second.
Therefore, the total number of desired outcomes is 9 + 9 = 18.
The total number of possible outcomes is the number of ways we could choose two parts from the box, which is the number of ways to choose 2 items from a set of 6 items. This is given by the formula:
Total outcomes = (6 choose 2) = (6! / (2! * 4!)) = 15
Putting it all together, we have:
Probability = (number of desired outcomes) / (total number of outcomes)
Probability = 18 / 15
Probability = 1.2
However, this answer doesn't make sense because probabilities should always be between 0 and 1. So we made a mistake somewhere. The mistake is that we double-counted some outcomes. For example, if we choose a bolt first and a nut second, this is the same as choosing a nut first and a bolt second, so we shouldn't count it twice.
To correct for this, we need to subtract the number of outcomes we double-counted. There are 3 outcomes that we double-counted: choosing two bolts, choosing two nuts, and choosing the same part twice (e.g. choosing the same bolt twice). So we need to subtract 3 from the total number of desired outcomes:
Number of desired outcomes = 18 - 3 = 15
Now we can calculate the correct probability:
Probability = (number of desired outcomes) / (total number of outcomes)
Probability = 15 / 15
Probability = 1
So the probability that one chosen part is a bolt and the other chosen part is a nut is 1, or 100%. This makes sense because if we choose two parts at random, we must get one bolt and one nut since there are three of each in the box.
learn more about probability
https://brainly.com/question/30034780
#SPJ11
Write 0.2 repeating as a fraction in simplest form.
Answers
Answer:
\(\frac{2}{9}\)
Step-by-step explanation:
We require to create 2 fractions with the repeating 2 after the decimal point.
let x = 0.22.... → (1) ← multiply both sides by 10
10x = 2.22....... → (2)
Subtract (1) from (2) thus eliminating the repeating decimal
9x = 2 ( divide both sides by 9 )
x = \(\frac{2}{9}\)
Thus
0.22..... = \(\frac{2}{9}\)
Answer:
2/9
Step-by-step explanation:
We require to create 2 fractions with the repeating 2 after the decimal point.
let x = 0.22.... → (1) ← multiply both sides by 10
10x = 2.22....... → (2)
Subtract (1) from (2) thus eliminating the repeating decimal
9x = 2 ( divide both sides by 9 )
x =
Thus
0.22..... =
Determine whether each expression is a polynomial. If so, identify the polynomial
as a monomial, binomial, or trinomial.

Answers
Answer:
1. is monomial
2. is binomial
3. is binomial
4. is trinomial
5. is trinomial
6. is binomial
Step-by-step explanation:
See...you need to know that the polynomial is determined by the number of unlilke terms in the expresion. i.e number of terms left that cant ne add subtracted or simplified anymore.
if its helpful send more quest om this...and domt forget brainliest
The expression shown are 1. Monomial 2. Not a polynomial 3. Binomial 4. Trinomial 5. Not a polynomial 6. Binomial
What is Polynomial?Polynomials are expressions of the form,
a₀ + a₁ x + a₂ x² + ................. + aₙ₋₁ xⁿ⁻1 + aₙ xⁿ
where a's are the coefficients, x is the variable and n is the number of terms.
1. 36
36 can be written as 36 x⁰.
This is a constant polynomial.
Since there is only one term, it is monomial.
2. \(\frac{3}{q^{2} }\) + 5
This can be written as 3 q⁻² + 5.
The exponent of the variable is not a whole number, so is not a polynomial.
3. 7x - x + 5
This can be written as 6x + 5.
This is a polynomial and is binomial since there are two terms.
4. 8g²h - 7gh + 2
This is a polynomial in two variables.
This is a trinomial, as there are three terms.
5. \(\frac{1}{4y^{2} }\) + 5y - 8
This can be written as 1/4 y⁻² + 5y - 8
This is not a polynomial as the exponent is not a whole number.
6. 6x + x²
This is a polynomial.
It is a binomial.
Hence four of the expressions shown are polynomials.
To learn more about Polynomials, click on the link :
https://brainly.com/question/11536910
#SPJ2
Tell me the correct answer I’m having trouble with this question

Answers
Consider the following hypothesis test: H0: p ? .75 Ha: p < .75 A sample of 300 items was selected. Compute the p-value and state your conclusion for each of the following sample results. Use ? = .05. Round your answers to four decimal places.
a. p = .68 p-value? Conclusion: p-value H0?
b. p = .72 p-value? Conclusion: p-value H0 ?
c. p = .70 p-value? Conclusion: p-value H0 ?
d. p = .77 p-value? Conclusion: p-value H0?
Answers
For each given sample result, the p-value and conclusion are as follows:
a. p-value = 0.0067, Conclusion: Reject H0, b. p-value = 0.0830, Conclusion: Fail to reject H0, c. p-value = 0.0322, Conclusion: Reject H0
d. p-value = 0.6221, Conclusion: Fail to reject H0
The p-value is a measure of the evidence against the null hypothesis (H0). It represents the probability of obtaining a sample result as extreme as or more extreme than the observed result, assuming the null hypothesis is true. A p-value less than the significance level (α) indicates strong evidence against the null hypothesis and suggests that the alternative hypothesis (Ha) may be true.
a. For p = .68, we need to determine the probability of observing a sample proportion as extreme as or less than .68, assuming the null hypothesis is true. By conducting the appropriate statistical test (e.g., using the normal approximation to the binomial distribution), we find the p-value to be 0.0067. Since the p-value is less than α = .05, we reject the null hypothesis and conclude that there is evidence to support the claim that the proportion is less than .75.
b. For p = .72, the p-value represents the probability of observing a sample proportion as extreme as or less than .72. Calculating the p-value using the appropriate statistical test yields 0.0830. Since the p-value is greater than α = .05, we fail to reject the null hypothesis. Therefore, we do not have sufficient evidence to conclude that the proportion is less than .75.
c. With p = .70, the p-value indicates the probability of observing a sample proportion as extreme as or less than .70. The calculated p-value is 0.0322. As the p-value is less than α = .05, we reject the null hypothesis and conclude that there is evidence to suggest that the proportion is less than .75.
d. For p = .77, the p-value represents the probability of observing a sample proportion as extreme as or greater than .77. After performing the necessary calculations, we find the p-value to be 0.6221. Since the p-value is much greater than α = .05, we fail to reject the null hypothesis. Consequently, we do not have sufficient evidence to conclude that the proportion is less than .75.
Learn more about statistical here: https://brainly.com/question/29000275
#SPJ11
A sinusoidal driving force is applied so that the forcing function is now f(t)=Fc​sin(100t/Ï„), where τ is the time constant that you calculated in (a). What is the amplitude of v(t) at steady-state? Choose the best answer. Note that K refers to the system gain that you calculated in (b). Briefly explain how you arrived at your answer. a. Amplitude =KFc​ b. Amplitude >KFc​ c. AmplitudeÂ
Answers
The amplitude of v(t) at steady-state is (a) Amplitude = KFc. This is because the amplitude of the response in a linear system is proportional to the amplitude of the forcing function, and the constant of proportionality is the system gain, K.
In this case, the forcing function has an amplitude of Fc, and the system gain is K, so the amplitude of the response at steady-state is K times Fc, or KFc. The amplitude of v(t) at steady-state can be found by considering the relationship between the system gain (K) and the forcing function f(t). Given the forcing function f(t) = Fc * sin(100t/τ), we can determine the steady-state response by taking the amplitude of the sinusoidal forcing function and multiplying it by the system gain K. Hence, the amplitude of v(t) at steady-state is: Amplitude = K * Fc Therefore, the best answer is: a. Amplitude = KFc.
Learn more about sinusoidal forcing function here: brainly.com/question/12060967
#SPJ11
Please help quick!!!!!
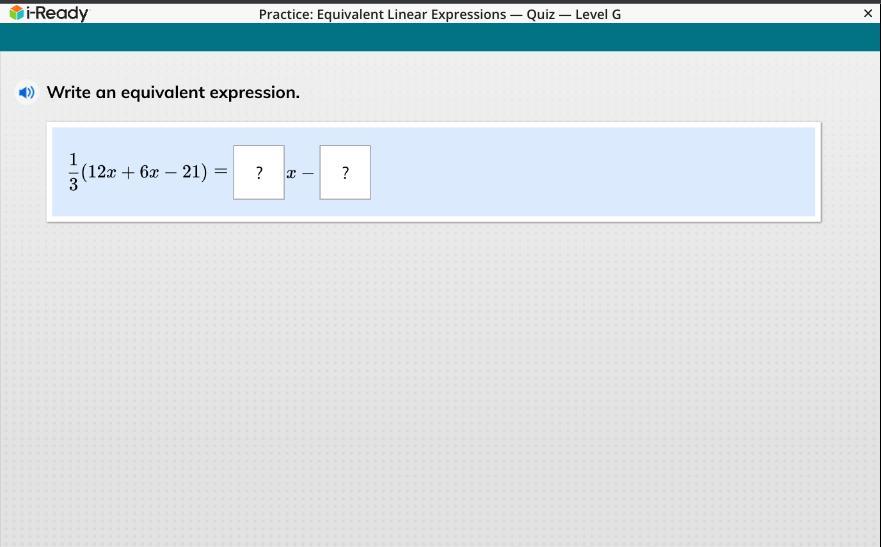
Answers
1/3(12x+6x-21) combine like terms
= 1/3(18x-21) distribute
= 6x - 7
if you increase an amount by 3 percent what is the single multiplyer
Answers
Answer:
1.03% is the answer
Step-by-step explanation:
-91.2e^(-0.5t)-19.6t+91.2=0
solve for t
Answers
The value of t after solving the equation -91.2e^(-0.5t)-19.6t+91.2=0 is 4.82.
Given:
-91.2e^(-0.5t) - 19.6t + 91.2 = 0
We need to find the value of 't' which satisfies the given equation.
In order to solve this equation, we can use Newton-Raphson method.
Newton-Raphson Method: Newton-Raphson method is used to find the root of the given equation.
The formula for Newton-Raphson method is given by x1 = x0 - f(x0) / f'(x0)
Where, x1 is the new value,
x0 is the old value,
f(x) is the function and
f'(x) is the derivative of the function.
f'(x) represents the slope of the curve at that particular point 'x'.
Let's find the derivative of the given function
f(t) = -91.2e^(-0.5t) - 19.6t + 91.2
f'(t) = -(-91.2/2)e^(-0.5t) - 19.6
Differentiate 91.2e^(-0.5t) using chain rule
=> 91.2 × (-0.5) × e^(-0.5t) = -45.6e^(-0.5t)
Now, we can rewrite the above equation as f(t) = -45.6e^(-0.5t) - 19.6t + 91.2
Using Newton-Raphson formula, we can find the value of t:
x1 = x0 - f(x0) / f'(x0)
Let's take x0 = 1x1 = 1 - f(1) / f'(1) = 1 - [-45.6e^(-0.5) - 19.6 + 91.2] / [-45.6 × (-0.5) × e^(-0.5) - 19.6]= 4.82
The value of t is 4.82.
To know more about equation refer here:
https://brainly.com/question/20420746
#SPJ11
how does DIAMETER of wire affect:
Strength
range
stiffness
Answers
The diameter of a wire significantly impacts its strength, range, and stiffness.
1. Strength: As the diameter of a wire increases, its overall strength improves. A larger cross-sectional area allows the wire to withstand greater forces before breaking. This is because the increased material can distribute force more effectively, resulting in enhanced tensile strength.
2. Range: The diameter of a wire also influences its range or length. Thicker wires tend to have shorter range capabilities compared to thinner wires. As the diameter increases, the weight and stiffness of the wire rise as well, making it harder to extend or coil over long distances. Conversely, thinner wires are more flexible and lightweight, enabling them to cover greater lengths.
3. Stiffness: Lastly, the diameter of a wire impacts its stiffness, which is the resistance of the wire to bending or deformation. With a larger diameter, the stiffness of the wire increases due to the higher amount of material present. This means that it requires more force to bend or change the shape of the wire, resulting in greater rigidity. On the other hand, wires with smaller diameters are more pliable and can easily be bent or manipulated.
In summary, the diameter of a wire plays a crucial role in determining its strength, range, and stiffness. Thicker wires exhibit enhanced strength and stiffness but may have limited range capabilities, while thinner wires are more flexible and suitable for longer distances but may not be as strong or rigid.
To learn more about tensile strength : brainly.com/question/14368662
#SPJ11
What is the x-intercept?

Answers
Answer:
y = 0.
Step-by-step explanation:
The x intercept is the point where the line crosses the x axis. At this point y = 0. ... To find the x intercept set y = 0.
Michael has a bag of marbles. The frequency of selecting each color is recorded in the table below.
Outcome Frequency
Green 4
Black 6
Orange 5
Based on the given frequency, determine the experimental probability of selecting an orange marble.
0.27
0.33
0.40
0.67
Answers
The probability of selecting an orange marble is 0.33.
Option B is the correct answer.
What is probability?It is the chance of an event to occur from a total number of outcomes.
The formula for probability is given as:
Probability = Number of required events / Total number of outcomes.
We have,
The number of times each marble is selected.
Green = 4
Black = 6
Orange = 5
Total number of times all marbles are selected.
= 4 + 6 + 5
= 15
Now,
The probability of selecting an orange marble.
= 5/15
= 1/3
= 0.33
Thus,
The probability of selecting an orange marble is 0.33.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ1
Maya bought 8 chicken wings for $8.80. If Maya spent $25.30, how many chicken wings did she buy?
Answers
Answer:
23
Step-by-step explanation:
Houa works at an electronics store as a salesperson. Houa earns a 4% commission on the total dollar amount of all phone sales she makes, and earns a 5% commission on all computer sales. Houa had $600 more in computer sales than in phone sales and earned a total of $129 in commission. Write a system of equations that could be used to determine the dollar amount of phone sales Houa made and the dollar amount of computer sales she made. Define the variables that you use to write the system.
Answers
The system of equations for determining the dollar amount of phone and computer sales are Sc = Sp + 600 and 0.05Sc + 0.04Sp = 1200
How to write a system of equations to determine the dollar amount of phone and computer sales?
A commission is defined as the compensation paid to a person or entity based on the sale of a product. It is calculated on a percentage basis
Given:
Phone sales commission = 4%
Computer sales commission = 5%
Total commission = $129
Let Sc and Sp represent the dollar amount of phone sales and computer sales respectively
If Houa had $600 more in computer sales than in phone sales, the equation can be written as:
Sc = Sp + 600
Since Houa earns a 4% commission on phone sales and a 5% commission on computer sales, and a total commission of $129. Thus, the equation for the commission can be written as:
0.05Sc + 0.04Sp = 1200
Note: 5% = 5/100 = 0.05 and 4% = 4/100 = 0.04
Therefore, the system of equations for determining phone and computer sales are Sc = Sp + 600 and 0.05Sc + 0.04Sp = 1200
Learn more about commission on:
https://brainly.com/question/24951536
#SPJ1
Use the Ratio Test to determine whether the series is convergent or divergent.
[infinity] 5
k!
sum.gif
k = 1
Answers
The series ∑ (k = 1 to infinity) 5^k / k! is convergent.
The Ratio Test is a method used to determine the convergence or divergence of a series by comparing the ratio of consecutive terms to a limit. For the given series, let's apply the Ratio Test:
Taking the ratio of consecutive terms:
|5^(k+1) / (k+1)!| / |5^k / k!|
Simplifying the expression:
|(5^(k+1) / (k+1)!) * (k! / 5^k)|
|5 / (k + 1)|
Now, we take the limit of this ratio as k approaches infinity:
lim(k->infinity) |5 / (k + 1)| = 0
Since the limit is less than 1, we can conclude that the series converges by the Ratio Test. In other words, the series ∑ (k = 1 to infinity) 5^k / k! is convergent.
The Ratio Test works by comparing the growth rate of consecutive terms in a series. If the ratio of consecutive terms approaches a value less than 1 as k goes to infinity, then the series converges. In this case, as the term k increases, the ratio 5 / (k + 1) approaches 0, indicating that the series converges.
Learn more about ratio test here:
https://brainly.com/question/20876952
#SPJ11
b. Is there a pattern in the table? Explain.
Answers
Answer:
no photo
Step-by-step explanation:
we need a photo to decide if answer is correct or not
WEATHER The temperature outside is
- 16°F. Then the temperature rises
20 degrees. What is the current outdoor
temperature?
Answers
Answer:
4 degrees Fahrenheit
Step-by-step explanation:
Answer:
negative four
Step-by-step explanation:
as discussed in class, if on any given day the dallas water district took 50 water samples can conducted the mpn tests. on that day the presumptive water tests at the water purification plant showed the following results: 97% of the water samples tested were free of any coliform bacteria. the remaining 3% of the samples had no more than 1 coliform per sample. what does this mean for you the consumer?
Answers
According to the EPA Clean Water Act regulations, all of the water that day is safe to drink.
To safeguard the standard of drinking water in the United States, the Safe Drinking Water Act (SDWA) was created. This legislation applies to all waters that are now or conceivably intended for consumption, whether they originate from above-ground or subsurface sources.
The Act mandates that all owners or operators of public water systems adhere to these fundamental (health-related) criteria and gives EPA the authority to set minimum standards to safeguard tap water.
The 1996 modifications to the SDWA mandate that while setting these criteria, EPA takes into account a thorough risk and cost evaluation as well as the finest peer-reviewed science.
The attainment of secondary standards is also encouraged by state governments, which may be authorized to implement these EPA regulations.
In accordance with the Act, EPA also establishes minimum requirements for state programs to safeguard underground water sources from being endangered by fluid injection underground.
To learn more about this problem:
https://brainly.com/question/2080178
#SPJ4
a quadratic equation in standard form is written ax2 = bx c, where a, b, and c are real numbers and a is not zero. True or False
Answers
The given statement is correct.
Hence it is true.
We have a statement regarding the quadratic equations.
We have to verify whether it is true or not.
Since we know that,
A quadratic equation is an equation with a single variable of degree 2. Its general form is ax² + bx + c = 0, where x is variable and a, b, and c are constants, and a ≠ 0.
According to the question, we are provided with the standard form of the quadratic equation as - ax² + bx + c = 0.
If we compare the statement given in the question with the definition discussed above, then it can be concluded that the given statement is true. Equation ax² + bx + c = 0 is the standard form of a quadratic equation with a, b, and c as constant real numbers.
The constant 'a' cannot be 0, as this would reduce the degree of the equation to 1.
Hence, the given statement is correct.
To learn more about quadratic equations, visit:
brainly.com/question/26090334
#SPJ12
a sphere has a radius of 6 feet. what are the dimensions of the cylinder with the greatest volume that can be inscribed in the sphere? what is the maximum volume of this cylinder?
Answers
The dimensions of the cylinder with the greatest volume that can be inscribed in the sphere are a height of 12 feet and a radius of 6 feet, and its maximum volume is approximately 1,152π cubic feet.
To find the dimensions of the cylinder with the greatest volume that can be inscribed in the given sphere, we need to consider the diameter of the sphere, which is twice the radius (12 feet). This diameter will be the height of the cylinder.
The maximum volume of the cylinder can be found by using the formula for the volume of a cylinder: V = πr^2h, where r is the radius of the cylinder and h is its height. Since the cylinder is inscribed in the sphere, its radius will be half of the diameter of the sphere, which is 6 feet. Therefore, we have:
V = π(6 feet)^2(12 feet) = 1,152π cubic feet
Learn more about diameter here:
brainly.com/question/13624974
#SPJ11
Help me on the questions please and thank you.

Answers
The lateral surface area of the rectangular prism is 308 units² and the total surface area is 398 units²
What is the lateral and total surface area of the rectangular prismThe formula of lateral surface area of the rectangular prism is given as;
LSA = 2(l +b)h
l = length b = breath or widthh = heightsubstituting the values into the formula;
LSA = 2(5 + 9) * 11
LSA = 308 units²
The total surface area is given by
TSA = 2(lb + bh + lh)
TSA = 2[(5*9) + (9*11) + (11*5)
TSA = 398 units²
Learn more on lateral surface area here;
https://brainly.com/question/15777841
#SPJ1
Find a sinusoidal function with the following four attributes: (1) amplitude is 10, (2) period is 5, (3) midline is y = 31, and (4) ƒ(3) = 41. f(x) = =
Answers
The sinusoidal function that satisfies the given attributes is f(x) = 10 * sin(2π/5 * x - π/5) + 31.
To find a sinusoidal function with the given attributes, we can use the general form of a sinusoidal function:
f(x) = A * sin(Bx + C) + D
where A represents the amplitude, B represents the frequency (related to the period), C represents the phase shift, and D represents the vertical shift.
Amplitude: The given amplitude is 10. So, A = 10.
Period: The given period is 5. The formula for period is P = 2π/B, where P is the period and B is the coefficient of x in the argument of sin. By rearranging the equation, we have B = 2π/P = 2π/5.
Midline: The given midline is y = 31, which represents the vertical shift. So, D = 31.
f(3) = 41: We are given that the function evaluated at x = 3 is 41. Substituting these values into the general form, we have:
41 = 10 * sin(2π/5 * 3 + C) + 31
10 * sin(2π/5 * 3 + C) = 41 - 31
10 * sin(2π/5 * 3 + C) = 10
sin(2π/5 * 3 + C) = 1
To solve for C, we need to find the angle whose sine value is 1. This angle is π/2. So, 2π/5 * 3 + C = π/2.
2π/5 * 3 = π/2 - C
6π/5 = π/2 - C
C = π/2 - 6π/5
Now we have all the values to construct the sinusoidal function:
f(x) = 10 * sin(2π/5 * x + (π/2 - 6π/5)) + 31
Simplifying further:
f(x) = 10 * sin(2π/5 * x - 2π/10) + 31
f(x) = 10 * sin(2π/5 * x - π/5) + 31
Therefore, the sinusoidal function that satisfies the given attributes is f(x) = 10 * sin(2π/5 * x - π/5) + 31.
Learn more about sinusoidal function here
https://brainly.com/question/29529184
#SPJ11
Simplify 4^3* 4^5 please help me

Answers
Answer:
C.
Step-by-step explanation:
add the numbers (power numbers)
=4^8
Consider the ratio of boys to girls of 4:5.
a) What is the total number of parts?
b) What fraction of the total are boys?
c) What fraction of the total are girls?
d)If there were 18 students in total,how many of them are boys?
e)If there were 18 students in total, how many of them are girls?
Answers
Step-by-step explanation:
\(a)\)
\(4+5=9 (parts)\)
\(b)\) our total is \(9\) our boys are \(4\\\)
our fraction is \(^4/_9\)
\(c)\) \(^5/_9\)
\(d)\) our whole used to be \(9\) but we doubled it so it is \(18\)
so we double \(4\) which equals \(8\)
\(^8/_{18}\)
\(e)\) \(^{10}/_{18}\)
Brainliest please
Passing through (3, -3) and perpendicular to y=3x+5
Answers
Answer:
Find the negative reciprocal of the slope of the original line and use the point-slope formula y−y1=m(x−x1) to find the line perpendicular to y=3x−5. y=−13x−2
Step-by-step explanation:

explain and solve thank u

Answers
The multiplication using Tape Diagram is $44.8
How to multiply numbers using Tape Diagram?A tape diagram is a pictorial model resembling a tape, that is used to assist with the calculation of addition, subtraction, multiplication, etc.
Given: 7 × $6.4
7 × $6.4 means $6.4 in 7 places. Thus, we can write that:
7 × $6.4 = $6.4 + $6.4 + $6.4 + $6.4 + $6.4 + $6.4 + $6.4 = $44.8
Check the attached picture for the Tape Diagram
Therefore, the multiplication 7×$6.4 gives $44.8
Learn more about Tape Diagram on:
https://brainly.com/question/2604125
#SPJ1

cary is 7 years older than dan. in 7 years the sum of their ages will be 75 . find the age of each man now. now in 7 years cary x 7 dan x x 7
Answers
Answer:
Cary is 70 and Dan is 61
Step-by-step explanation:
c = Cary's age
d= Dan's age
c+d+7=75
C= d+7
Rewrite this with one variable
d+7+d+7=75
Simplify and solve for d (dan's current age)
d +14 = 75
d = 61
Cary is 7 years older, so just add 7 to Dan's age, resulting in 70.
Hope this helps! If it was pls give brainliest.
PLZ I NEED HELP I HAVE 15 MIN LEFT I WILL GIVE BIG BRAINLYEST TO WHOEVER ANSWERS FIRST AND RIGHT
The least common multiple of the two numbers is 36. Which could be the two numbers?
9 and 12
4 and 6
3 and 8
3 and 12
Answers
Answer:
4 and 6
Step-by-step explanation:
The lest lol