Answers
The value of the error will be 0.20. The discrepancy between the calculated value and the correct value is referred to as an "error" in statistics.
What is the error?An error is a mistaken or erroneous action. In some contexts, an error is interchangeable with a mistake.
Given equation;
2x³+7x²+3 = 0
The value of the x from the above equation is;
x + 3.61479523 = 0
x= - 3.61479523
The error is found as;
\(\rm error = \frac{-3.61 -(-3)}{-3} \\\\ error = 0.20\)
Hence. the value of the error will be 0.20.
To learn more about the error refer to the link;
https://brainly.com/question/13286220
#SPJ1
Related Questions
Sneha went to a park 150m long and 80m wide. She took one complete round on its boundary. What is the distance covered by Sneha?
Answers
Answer:
Since she takes one complete round which is equal to perimeter of the rectangular park. Therefore, the distance covered by her is 460m.
6. Journalise the following transactions
1. Bricks for Rs 60,000 and timber for Rs 35,000 purchased for
the construction of building. The payment was made by cheque.
2. Placed in fixed deposit account at bank by transfer from current
account Rs 13,000.
3. Appointed Mr. S.N. Rao as Accountant at Rs 300 p.m. and
Received Rs 1000 as security Deposit at 5% p.a. interest.
4. Sold goods to shruti for Rs 80,000 at 15% trade discount and
4% cash discount. Received 75% amount immediately through a
cheque.
5. Purchased goods from Richa for Rs 60,000 at 10% trade
discount and 5% cash discount. 60% amount paid by cheque
immediately.
6.
On 18th jan,Sold goods to shilpa at the list price of Rs 50,000
20% trade discount and 4% cash discount if the payment is made
within 7 days. 75% payment is received by cheque on Jan 23rd.
7. On 25th jan, sold goods to garima for Rs 1,00,000 allowed her
20% trade discount and 5% cash discount if the payment is made
within 15 days. She paid 1/4th of the amount by cheque on Feb 5th
and 60% of the remainder on 15th in cash.
8. Purchased land for Rs 2,00,000 and paid 1% as brokerage and
Rs 15,000 as registration charges on it. Entire payment is made by
cheque.
9. Goods worth Rs 25,000 and cash Rs 40,000 were taken away
by the proprietor for his personal use.
10. Sold goods costing Rs 1,20,000 to charu at a profit of 33% 3 %
on cost less 15% trade discount.
9
11. Paid rent of building Rs 60,000 by cheque. Half the building is
used by the proprietor for residential purpose.
12. Sold goods costing Rs 20,000 to sunil at a profit of 20% on
sales less 20% trade discount .
13. Purchased goods for Rs 1000 from nanda and supplied it to
helen for Rs 1300. Helen returned goods worth Rs 390, which in
turn were returned to nanda.
14. Received invoice at 10% trade discount from rohit and sons
and supplied these goods to madan, listed at Rs 3000.
Answers
1.Bricks and timber purchased for construction. (Debit: Bricks - Rs 60,000, Debit: Timber - Rs 35,000, Credit: Bank - Rs 95,000)
2.Transfer of Rs 13,000 to fixed deposit account. (Debit: Fixed Deposit - Rs 13,000, Credit: Current Account - Rs 13,000)
3.Appointment of Mr. S.N. Rao as Accountant. (Debit: Salary Expense - Rs 300, Debit: Security Deposit - Rs 1,000, Credit: Accountant - Rs 300)
4.Goods sold to Shruti with discounts. (Debit: Accounts Receivable - Shruti - Rs 80,000, Credit: Sales - Rs 80,000)
5.Goods purchased from Richa with discounts. (Debit: Purchases - Rs 60,000, Credit: Accounts Payable - Richa - Rs 60,000)
6.Goods sold to Shilpa with discounts and received payment. (Debit: Accounts Receivable - Shilpa - Rs 50,000, Credit: Sales - Rs 50,000)
7.Goods sold to Garima with discounts and received partial payment. (Debit: Accounts Receivable - Garima - Rs 1,00,000, Credit: Sales - Rs 1,00,000)
8.Purchase of land with additional charges. (Debit: Land - Rs 2,00,000, Debit: Brokerage Expense - Rs 2,000, Debit: Registration Charges - Rs 15,000, Credit: Bank - Rs 2,17,000)
9.Proprietor took goods and cash for personal use. (Debit: Proprietor's Drawings - Rs 65,000, Credit: Goods - Rs 25,000, Credit: Cash - Rs 40,000)
10.Goods sold to Charu with profit and discount. (Debit: Accounts Receivable - Charu - Rs 1,20,000, Credit: Sales - Rs 1,20,000)
11.Rent paid for the building. (Debit: Rent Expense - Rs 60,000, Credit: Bank - Rs 60,000)
12.Goods sold to Sunil with profit and discount. (Debit: Accounts Receivable - Sunil - Rs 24,000, Credit: Sales - Rs 24,000)
13.Purchased goods from Nanda and supplied to Helen. (Debit: Purchases - Rs 1,000, Debit: Accounts Payable - Nanda - Rs 1,000, Credit: Accounts Receivable - Helen - Rs 1,300, Credit: Sales - Rs 1,300)
14.Purchased goods from Rohit and Sons and supplied to Madan. (Debit: Purchases - Rs 2,700, Credit: Accounts Payable - Rohit and Sons - Rs 2,700, Debit: Accounts Receivable - Madan - Rs 3,000, Credit: Sales - Rs 3,000)
Here are the journal entries for the given transactions:
1. Bricks and timber purchased for construction:
Debit: Bricks (Asset) - Rs 60,000
Debit: Timber (Asset) - Rs 35,000
Credit: Bank (Liability) - Rs 95,000
2. Transfer to fixed deposit account:
Debit: Fixed Deposit (Asset) - Rs 13,000
Credit: Current Account (Asset) - Rs 13,000
3. Appointment of Mr. S.N. Rao as Accountant:
Debit: Salary Expense (Expense) - Rs 300
Debit: Security Deposit (Asset) - Rs 1,000
Credit: Accountant (Liability) - Rs 300
4. Goods sold to Shruti:
Debit: Accounts Receivable - Shruti (Asset) - Rs 80,000
Credit: Sales (Income) - Rs 80,000
5. Goods purchased from Richa:
Debit: Purchases (Expense) - Rs 60,000
Credit: Accounts Payable - Richa (Liability) - Rs 60,000
6. Goods sold to Shilpa:
Debit: Accounts Receivable - Shilpa (Asset) - Rs 50,000
Credit: Sales (Income) - Rs 50,000
7. Goods sold to Garima:
Debit: Accounts Receivable - Garima (Asset) - Rs 1,00,000
Credit: Sales (Income) - Rs 1,00,000
8.Purchase of land:
Debit: Land (Asset) - Rs 2,00,000
Debit: Brokerage Expense (Expense) - Rs 2,000
Debit: Registration Charges (Expense) - Rs 15,000
Credit: Bank (Liability) - Rs 2,17,000
9. Goods and cash taken away by proprietor:
Debit: Proprietor's Drawings (Equity) - Rs 65,000
Credit: Goods (Asset) - Rs 25,000
Credit: Cash (Asset) - Rs 40,000
10. Goods sold to Charu:
Debit: Accounts Receivable - Charu (Asset) - Rs 1,20,000
Credit: Sales (Income) - Rs 1,20,000
Credit: Cost of Goods Sold (Expense) - Rs 80,000
Credit: Profit on Sales (Income) - Rs 40,000
11. Rent paid for the building:
Debit: Rent Expense (Expense) - Rs 60,000
Credit: Bank (Liability) - Rs 60,000
12. Goods sold to Sunil:
Debit: Accounts Receivable - Sunil (Asset) - Rs 24,000
Credit: Sales (Income) - Rs 24,000
Credit: Cost of Goods Sold (Expense) - Rs 20,000
Credit: Profit on Sales (Income) - Rs 4,000
13. Goods purchased from Nanda and supplied to Helen:
Debit: Purchases (Expense) - Rs 1,000
Debit: Accounts Payable - Nanda (Liability) - Rs 1,000
Credit: Accounts Receivable - Helen (Asset) - Rs 1,300
Credit: Sales (Income) - Rs 1,300
14. Goods received from Rohit and Sons and supplied to Madan:
Debit: Purchases (Expense) - Rs 2,700 (after 10% trade discount)
Credit: Accounts Payable - Rohit and Sons (Liability) - Rs 2,700
Debit: Accounts Receivable - Madan (Asset) - Rs 3,000
Credit: Sales (Income) - Rs 3,000
for such more question on journal entries
https://brainly.com/question/28390337
#SPJ8
Help me with this question please

Answers
Answer: C
Step-by-step explanation:
Y=2x-4
8=2(6)-4
8=12-4
8=8 Correct
a person invested $6300 for 1 year part at 8% part at 10% and the remainder at 15%. The total annual income from these investments was $773. The amount of money invested at 15% was $300 more than the amounts invested at 8% and 10% combined. Find the amount invested at each rate.
Answers
Answer:
8%: $295
10% : $6005
15%: $595
Step-by-step explanation:
The total invested amount was $6300The total annual income from the investments was $773The amount invested at 15% was $300 more than the amounts invested at 8% and 10% combinedLet's break this down:
Let's call the amounts invested at 8% and 10% combined = x
Then call the amount invested at 15% = x + $300
8% of x = 0.08x
10% of (6300 - x) = 0.1(6300 - x)
15% of (x + $300) = 0.15(x + $300)
0.08x + 0.1(6300 - x) + 0.15(x + $300) = $773
0.18x = $53
x = $53/0.18 = $295
a = amount invested at 8%
how much is 8% of "a"? (8/100) * "a", namely 0.08a.
b = amount invested at 10%
how much is 10% of "b"? (10/100) * "b", namely 0.10b.
c = amount invested at 15%
how much is 15% of "c"? (15/100) * "c", namely 0.15c.
we know the total amount invested is 6300, so whatever "a", "b" and "c" might be, we know that a + b + c = 6300.
we also know that the yielded amount in interest is 773, so if we simply add their interest, that'd be 0.08a + 0.10b + 0.15c = 773.
we also know that the combined amounts of "a + b" plus 300 bucks is "c", so really c = a + b + 300.
\(c = a + b + 300 \\\\[-0.35em] ~\dotfill\\\\ a+b+c=6300\implies c=6300-a-b\implies \stackrel{\textit{substituting from the equation above}}{a+b+300=6300-a-b} \\\\\\ 2a+2b+300=6300\implies 2a+2b=6000\implies 2(a+b)=6000\)
\(a+b=\cfrac{6000}{2}\implies a+b=3000\implies \boxed{b=3000-a} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{since we know that}}{c = a + b + 300}\implies \stackrel{\textit{substituting from above}}{c=a+(3000-a)+300}\implies {\Large \begin{array}{llll} c=3300 \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{ \textit{we also know that} }{0.08a+0.10b+0.15c=773}\implies \stackrel{\textit{now, substituting "b" and "c"}}{0.08a+0.10(3000-a)+0.15(3300)=773}\)
\(0.08a+300-0.10a+495=773\implies -0.02a+300+495=773 \\\\\\ -0.02a+795=773\implies -0.02a=-22\implies a=\cfrac{-22}{-0.02}\implies {\Large \begin{array}{llll} a=1100 \end{array}} \\\\\\ \stackrel{\textit{now, we know that}}{b=3000-a}\implies {\Large \begin{array}{llll} b=1900 \end{array}}\)
Consider the line 5x+2y=−4. What is the equation of the line parallel to the given line that passes through the point (−2, 6) in slope-intercept form? Enter your answer by filling in the boxes to complete the equation.
Answers
Answer:
y = -5/2x +1
Step-by-step explanation:
You want the slope-intercept form equation for the line through the point (-2, 6) that is parallel to 5x +2y = -4.
Parallel lineThe equation of a parallel line can be the same as the given equation, except for the constant. The new constant can be found by substituting the given point coordinates:
5(-2) +2(6) = c
-10 +12 = c
2 = c
Now we know the equation of the parallel line can be written as ...
5x +2y = 2
Slope-intercept formSolving for y puts this in slope-intercept form:
2y = -5x +2 . . . . . . . . subtract 5x
y = -5/2x +1 . . . . . . . . divide by 2
We don't know what your boxes look like, but we can separate the numbers to make it look like this:
\(\boxed{y=\dfrac{-5}{2}x+1}\)
#95141404393

nicholas wants to buy a cd for $200 that earns 3% apr and is compounded quarterly. the cd matures in 5 years. his interest earned will not be reinvested in the cd.what will nicholas total interest be at the date of maturation?
Answers
Answer: 30
Step-by-step explanation:
Answer:
the correct answer is $1.50 for me
Step-by-step explanation:
st took the quiz and got this question correct, hope this helps!
David uses 2/3 cup of milk to make a batch of muffins. He wants to make 12 batches of muffins for a fundraiser. How much milk does he need to make all 12 batches? Answers: 8, 1, 10, 16
Answers
Answer:
10
Step-by-step explanation:
Let’s assume that 41% of Californians have been to Disneyland. A random sample of 6 Californians are chosen and asked if they have ever been to Disneyland.
a) Define a random variable X for this situation.
b) Is X binomial or geometric or neither? Explain.
c) Out of the 6 people asked, with is the probability that exactly 3 have been to Disneyland?
d) What is the mean of X?
e) What is the standard deviation of X?
f) What is the probability that the number of Californians in this sample that have been to Disneyland is within one standard deviation of the mean?
Answers
a) Let X represent the random variable of the number of Californians in the sample of 6 people who have been to Disneyland.
b) X is a binomial random variable because it records the number of successes (people who have been to Disneyland) in a fixed number of trials (6 people).
c) The probability =3.05.
d) The mean of X is 2.46.
e) The standard deviation of X is 1.2.
f) The probability 68.27%.
What is standard deviation?It is used to measure the spread of data around the mean or expected value.
a) Let X represent the random variable of the number of Californians in the sample of 6 people who have been to Disneyland.
b) X is a binomial random variable because it records the number of successes (people who have been to Disneyland) in a fixed number of trials (6 people).
c) The probability of exactly 3 people having been to Disneyland is 3.05.
This is calculated using the binomial probability formula:
P(x=3) = (6³) * (0.41³) * (0.59³)
= 3.05
d) The mean of X is 2.46. This is calculated using the binomial mean formula:
μ = n * p
= 6 * 0.41
= 2.46
e) The standard deviation of X is 1.2. This is calculated using the binomial standard deviation formula:
σ = √[n * p * (1 - p)]
= √[6 * 0.41 * (1 - 0.41)]
= 1.2
f) The probability that the number of Californians in the sample that have been to Disneyland is within one standard deviation of the mean is 68.27%.
This is calculated using the standard normal distribution z-score formula:
P(1.19<z<2.73) = 0.6827
For more questions related to mean
https://brainly.com/question/26941429
#SPJ1
As reported in Trends in Television, the proportion of US households who have at least one VCR is 0.535. If 14 households are selected at random, without replacement, from all US households, what is the (approximate) probability that the number having at least one VCR is no more than 8 but at least 6.00. Be sure to use many decimal places in your calculations (at least 4), but report your answer to three decimal places.
Answers
Using the binomial distribution, it is found that there is a 0.5601 = 56.01% probability that the number having at least one VCR is no more than 8 but at least 6.00.
For each household, there are only two possible outcomes. Either it has at least one VCR, or it does not. The probability of a household having at least one VCR is independent of any other household, which means that the binomial distribution is used to solve this question.
Binomial probability distribution
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
The parameters are:
x is the number of successes. n is the number of trials. p is the probability of a success on a single trial.In this problem:
14 households, hence \(n = 14\).0.535 probability of having at least one VCR, hence \(p = 0.535\).The probability of at least 6 and no more than 8 is:
\(P(6 \leq X \leq 8) = P(X = 6) + P(X = 7) + P(X = 8)\)
In which:
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 6) = C_{14,6}.(0.535)^{6}.(0.465)^{8} = 0.1539\)
\(P(X = 7) = C_{14,7}.(0.535)^{7}.(0.465)^{7} = 0.2024\)
\(P(X = 8) = C_{14,8}.(0.535)^{8}.(0.465)^{6} = 0.2038\)
Then:
\(P(6 \leq X \leq 8) = P(X = 6) + P(X = 7) + P(X = 8) = 0.1539 + 0.2024 + 0.2038 = 0.5601\)
0.5601 = 56.01% probability that the number having at least one VCR is no more than 8 but at least 6.00.
A similar problem is given at https://brainly.com/question/24863377
Select the correct answer. What is the end behavior of the cube root function represented by this graph? The graph of radical function passes through (minus 5, 2), (3, minus 2), and (6, minus 5) also intercepts the x-axis at 2 units and y-axis at 1 unit A. As x decreases in value, decreases in value. As x increases in value, increases in value. B. As x decreases in value, increases in value. As x increases in value, increases in value. C. As x decreases in value, increases in value. As x increases in value, decreases in value. D. As x decreases in value, decreases in value. As x increases in value, decreases in value.
Answers
The end behavior of the cube root function represented by the graph is B. As x decreases in value, f ( x ) increases in value. As x increases in value, f ( x ) decreases in value.
The given data is
(-5, 2)
(0, 1) = y-axis at 1 unit
(2, 0) = intercepts the x-axis at 2 units
(3, -2)
(6, -5)
Examining the increasing and decreasing trend as represented by the ordered pairs it shows that
x ⇒ -∞ f(x) ⇒ ∞
x ⇒ ∞ f(x) ⇒ -∞
This end behavior is described by option B.
Learn more about end behavior here:
brainly.com/question/28954897
#SPJ1
john wants to purchase a boat that costs $1,500. He signs an installment agreement requiring a 20% down payment. How much will john need for the down payment
Answers
Answer:
$300 down payment
Step-by-step explanation:
John wants to purchase a boat that costs $1,500. He signs an installment agreement requiring a 20% down payment. How much will john need for the down payment
20% = 0.20
0.20 * 1,500 = $300 down payment
Solve 12x + 4y = 20 for y.
A. y=-3x+ 20
B. y = -12x+ 20
C. y= 12x+ 5
D. y=-3x+ 5
Answers
Answer:
D. y= -3x+ 5
Step-by-step explanation:
\(12x + 4y = 20\)
Move 12x to the right and change its sign
\(4y =20-12x\)
Divide through by 4
\(\frac{4y}{4} = \frac{20}{4} -\frac{12x}{4} \\\\Simplify\\y = 5-3x\\y =-3x+5\)
Answer:
\( \boxed{ \bold{ \huge{ \boxed{ \sf{y = - 3x + 5}}}}}\)
Option D is the correct option.
Step-by-step explanation:
\( \sf{12x + 4y = 20}\)
Move 12x to right hand side and change it's sign
⇒\( \sf{4y = - 12x + 20}\)
Divide both sides of the equation by 4
⇒\( \sf{ \frac{4y}{y} = \frac{ - 12x + 20}{4} }\)
⇒\( \sf{y = \frac{ - 12x}{4} + \frac{20}{4} }\)
Divide -12x by 4 . Also divide 20 by 4
⇒\( \sf{y = - 3x + 5}\)
Hope I helped!
Best regards!! :D
Shelton mix 1 1/4 cups of purple cabbage and
2 3/8 cups of lettuce to make a big salad. Each day he eats 3/4 of a cup is salad.

Answers
Answer:
Its the bottom one.
Step-by-step explanation:
Answer: ( 1 1/4 + 2 3/8 ) 3/4
Step-by-step explanation:
This is the answer
45 cows can graze a field in 13 days. How many cows will graze the same field in 9 days
Answers
Answer:
65 cows
Step-by-step explanation:
Inverse rule of three
\(45-------13\\x -------- 9\)
\(x=\frac{(45)(13)}{9}=585/9=65\)
Hope this helps
A poker hand is a set of 5 cards randomly chosen from a deck of 52 cards. Find the probability of a (a) royal flush (ten, jack, queen, king, ace in a single suit). (b) straight flush (five in a sequence in a single suit, but not a royal flush). (c) four of a kind (four cards of the same face value). (d) full house (one pair and one triple, each of the same face value). (e) flush (five cards in a single suit but not a straight or royal flush). (f) straight (five cards in a sequence, not all the same suit). (Note that in straights, an ace counts high or low.) g
Answers
Answer:
a) 0.000001539
b) 0.00001385
c) 0.0002401
d) 0.001441
e) 0.001966
Step-by-step explanation:
Since there are 52 deck of cards, and the hand of the poker is 5 set, then the total number of hands achievable would be
T = 52! / 5!(52 - 5)!
T = 52! / 5! 47 !
T = 2598560 possibilities.
a) There are 4 ways of getting a royal flush. So the probability of getting a royal flush is
4 / 2598560 =
0.000001539
b) There are 9 hands from the 5 card hands, and also, there are 4 possible suits. So then, the probability is
9 * 4 / 2598560 =
36 / 2598560 =
0.00001385
c) There are 13 possible ways to get a four of a kind, since there are 5 cards with the poker, the remaining would be taken from the 48 remaining cards, thus
13 * 48 / 2598560 =
624 / 2598560 =
0.0002401
d) 3 of a kind in conjunction with a pair is needed to form a full house. This 3 of a kind can be gotten from any 4 suits. Then again, the pair has two cards with the same face value. So,
4! / 2! (4 - 2)! =
4! / 2! 2! = 6
That means, there are 6 possible ways to get our needed suits. Then, the probability of getting a full house is
13 * 4 * 12 * 6 / 2598560 =
3744 / 2598560 =
0.001441
e) To get a flush, all the 5 cards in the hand needs to have the same suit. Now, there are 13 different types of cards with only 5 cards being in the hand, thus
13! / 5! (13 - 5)! =
13! / 5! 8! = 1287
Now, recall that the question specifically asked us not to include any straight. There are 10 straights that can be gotten, and thus, we subtract it.
1287 - 10 = 1277
Since there are 4 suits, the probability of getting a flush is
1277 * 4 / 2598560 =
5108 / 2598560 = 0.001966
wenty-five randomly selected students were asked the number of movies they watched the previous week. the results are as follows:
Answers
The sample mean of the number of movies watched by 25 students is 2.8 and the approximate sample standard deviation is 1.15.
(a) The sample mean X can be calculated by taking the average of the number of movies watched by all 25 students.
Step 1: Sum up the number of movies watched by all 25 students:
\(0 * 1 + 1 * 2 + 2 * 4 + 3 * 10 + 4 * 6 + 3 * 2 = 0 + 2 + 8 + 30 + 24 + 6 = 70\)
Step 2: Divide the sum from Step 1 by the number of students (25):
70 / 25 = 2.8
So the sample mean X = 2.8
(b) The sample standard deviation s can be calculated using the formula:
\(s = \sqrt{\frac{ \sum(X - X_{mean})^2}{(n-1)} }\)
Where \(X_{mean}\) is the sample mean, n is the sample size, and Σ represents the sum of all values.
Step 1: Calculate \((X - X_{mean})^2\)for each data point and sum up the values:
\((0 - 2.8)^2 * 1 + (1 - 2.8)^2 * 2 + (2 - 2.8)^2 * 4 + (3 - 2.8)^2 * 10 + (4 - 2.8)^2 * 6 + (3 - 2.8)^2 * 2\\ = 7.84 + 3.24 + 0.64 + 9.6 + 1.44 + 7.84\\ = 31.36\)
Step 2: Divide the sum from Step 1 by (n - 1) = 24:
31.36 / 24 = 1.31
Step 3: Take the square root of the result from Step 2:
\(\sqrt{1.31} = 1.15\)
So the approximate sample standard deviation s = 1.15 (rounded to two decimal places).
Learn more about deviation :
https://brainly.com/question/23907081
#SPJ4
need help really please someone

Answers
Answer:
5/6 x 1 = 5/6 2/3 x 2= 4/6. 5/6 is greater than
2/3
Step-by-step explanation:
find a common denominator then see which one has more value
Area of composite shapes, There is a pair of parallel sides in the following shape.
What is the area of the shape?

Answers
The following form has two parallel sides, and, in accordance with the provided assertion, its area is 21 cm².
What does mathematicians mean by area?Area is the entire amount of space occupied by a flattened (2-D) surface or form of an item. The area of a planar figure is the space that its perimeter encloses. The quantity of unit rectangles that completely encircle a closed figure's surface is its area. Square units such as cm² and m² are used to measure area.
The ratio will also be 1/2 * (bases 1 + base 2) * length since it is a trapezium.
So, 1/2 * ( 9+5) * 3
= 1/2 * 14 * 3
= 1/2 * 42
= 21 cm²
To know more about Area visit:
https://brainly.com/question/17335144
#SPJ1
I have another riddle.
If you buy one rabbit and a rabbit can produce 5 per year, then how many rabbits will you have in 9 years?
Answers
Total number of rabbits produced in 9 years will be 45.
What is Equation Modelling?
Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem.
Given is a rabbit can produce 5 new rabbits per year
Total number of rabbits produced in 9 years will be -
n = 5y = 5 x 9 = 45 new rabbits
Therefore, total number of rabbits produced in 9 years will be 45.
To solve more questions on equation modelling, visit the link below-
brainly.com/question/6593383
#SPJ1
Translate the verbal expression into an algebraic expression "Four times the sum of a number and 5"?
Answers
Answer:
4(x+5)
Step-by-step explanation:
Algebra Question
A company rents moving trucks out of two locations: Detroit and San Antonio. Some of their customers rent a truck in one city and return it in the other city, and the rest of their customers rent and return the truck in the same city. The company owns a total of 400 trucks.
The company has seen the following trend:
About 70 percent of the trucks in Detroit move to San Antonio each week.
About 55 percent of the trucks in San Antonio move to Detroit each week.
Suppose right now Detroit has 140 trucks.
How many trucks will be in each city after 1 week? [Round answers to the nearest whole number.]
Detroit:
San Antonio:
How many trucks will be in each city after 4 weeks? [Round answers to the nearest whole number.]
Detroit:
San Antonio:
If the vector [te\(\left[\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right]\) resents the distribution of trucks, where x1 is the number in Detroit and x2 is the number in San Antonio, find the matrix A so that At is the distribution of trucks after 1 week.
Answers
Answer:
After 4 weeks, there will be approximately 66 trucks in Detroit and 334 trucks in San Antonio.
Step-by-step explanation:
To solve this problem, we can use matrix multiplication to find the distribution of trucks after a given number of weeks. Let's start by calculating the distribution after 1 week.
Given:
- Total number of trucks: 400
- Number of trucks in Detroit (initially): 140
- About 70% of the trucks in Detroit move to San Antonio each week.
- About 55% of the trucks in San Antonio move to Detroit each week.
To calculate the distribution after 1 week, we can set up the following matrix equation:
[x1_new] [0.3 0.55] [x1]
[x2_new] = [0.7 0.45] * [x2]
Here, [x1_new, x2_new] represents the distribution of trucks after 1 week, and [x1, x2] represents the initial distribution.
To find the matrix A, we need to determine the coefficients based on the given percentages:
A = [0.3 0.55]
[0.7 0.45]
After finding matrix A, we can calculate A^t to represent the distribution after t weeks.
Now, let's calculate the distribution after 1 week and 4 weeks, rounding the answers to the nearest whole number:
After 1 week:
[x1_new] [0.3 0.55] [140] ≈ [62]
[x2_new] = [0.7 0.45] * [260] ≈ [338]
After 4 weeks:
[x1_new] [0.3 0.55] [62] ≈ [66]
[x2_new] = [0.7 0.45] * [338] ≈ [334]
So, after 1 week, there will be approximately 62 trucks in Detroit and 338 trucks in San Antonio.
After 4 weeks, there will be approximately 66 trucks in Detroit and 334 trucks in San Antonio.
Please note that the calculations provided are approximate, as rounding was done at each step.
determine the value of x

Answers
The measure of the missing side length x in the right triangle is 1.5.
What is the measure of side length x?The figure in the image is a right triangle having one of its interor angle at 90 degree.
From the diagram;
Let angle θ = 30 degree
Opposite angle θ = x
Hypotenuse = 3
To solve for the missing side length x, we use the trigonometric ratio.
Note that: sine = opposite / hypotenuse
Hence:
sin( θ ) = opposite / hypotenuse
Plug in the values:
sin( 30 ) = x / 3
x = sin( 30 ) × 3
x = 1.5
Therefore, the value of x is 1.5.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
use the sketch below to decide if congruence can be proved, and if so, which method would prove the congruence.
Answers
Yes, the proof of congruence of two triangles ∆ABC ≅ ∆GHF is possible.
The convergence method which proves this congruence is SSS(side-side-side) congruence.
We have given the sketch of two triangles as seen above. We have to prove ∆ABC ≅ ∆GHF
Now , AB = √(-7+7)² + 5² = 5 in triangle ABC and FG = 5 in triangle FGH,
so, AB ≅ FG
Because AC = 3 in triangle ABC and FH = 3 in triangle FGH,
so, AC ≅ FH
To find the lengths of BC and GH , we can use distance formula.
Length of BC :
BC = √[(x₂ - x₁)² + (y₂ - y₁)²]
(x₁, y₁) = B(-7, 0) and (x₂, y₂) = C(-4, 5).
BC = √[(-4 + 7)² + (5 - 0)²]
= √[32 + 52]
= √[9 + 25]
= √34
Length of GH :
GH = √[(x₂ - x₁)² + (y₂ - y₁)²]
(x₁, y₁) = G(1, 2) and (x₂, y₂) = H(6, 5).
GH = √[(6 - 1)² + (5 - 2)²]
= √[52 + 32]
= √[25 + 9]
= √34
Conclusion :because BC = √34 and GH = √34,
=>BC ≅ GH
All the three sides of one triangle is congruent to the corresponding sides of other triangle.
By SSS congruence postulate,
ΔABC ≅ ΔFGH
To learn more about SSS (Side-Side- Side ) Congruence postulate , refer:
https://brainly.com/question/24079210
#SPJ4

Anna has I nickels and y dimes. She has at most 22 coins worth a minimum of $1.40combined. Solve this system of inequalities graphically and determine one possiblesolution.Inequality 1:yplastInequality 2: y2plot882624NO1816141210864202 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40Anna could havenickels anddimes.Submit Answer
Answers
Here, there are x nickels and y dimes
At most, they are 22 in number;
Mathematically;
x + y ≤ 22
y ≤ 22 - x
The above is the first inequality
A nickel is worth 5 cents while a dime is worth 10 cents
So the worth of x nickels is 5x cents
The worth of y dimes is 10y cents
Kindly note that $1.40 is same as 140 cents
So the sum of both is at least 140 cents
5x + 10y ≥ 140
10y ≥ 140 - 5x
Now divide both sides by 10
y ≥ 14 - 0.5x
So the two inequalities to solve simultaneously are;
y ≤ 22 - x and y ≥ 14 - 0.5x
Can you help with this question? I am kinda stuck.

Answers
Answer:
29400 cm²Step-by-step explanation:
The cube has 6 equal faces.
Total surface area:
S = 6a²S = 6*(0.7 m)² = 6*(70 cm) ² = 29400 cm²Assume that a population is normally distributed with a mean of 100 and a standard deviation of 15. Would it be unusual for the mean of a sample of 3 to be 115 or more? Why or why not?
Answers
Answer:
|Z| < 2, which means that it would not be unusual for the mean of a sample of 3 to be 115 or more.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
If \(|Z| > 2\), the value of X is considered to be unusual.
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Assume that a population is normally distributed with a mean of 100 and a standard deviation of 15.
This means that \(\mu = 100, \sigma = 15\)
Sample of 3
This means that \(n = 3, s = \frac{15}{\sqrt{3}}\)
Would it be unusual for the mean of a sample of 3 to be 115 or more? Why or why not?
We have to find the z-score.
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{115 - 100}{\frac{15}{\sqrt{3}}}\)
\(Z = 1.73\)
|Z| < 2, which means that it would not be unusual for the mean of a sample of 3 to be 115 or more.
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
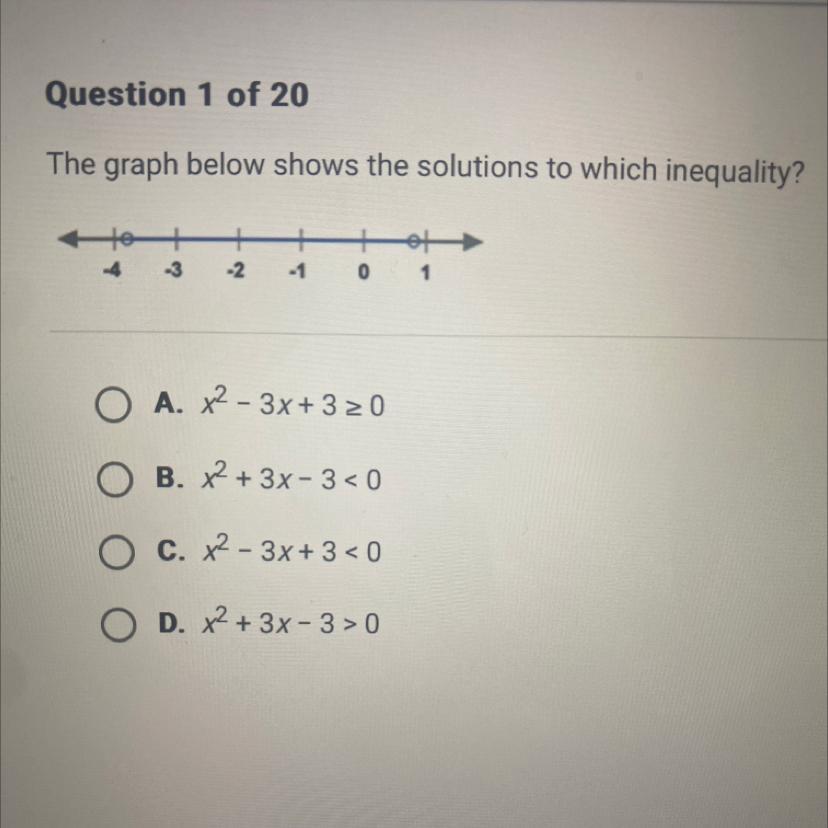
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
Question 6 of 10
What is the solution to the system of equations graphed below?
y = -2x + 4
y=x-5
Answers
Answer:
the solution to the system of equations is (x, y) = (3, -2).
Step-by-step explanation:
y = -2x + 4 (Equation 1)
y = x - 5 (Equation 2)
To solve for x, we can equate the right sides of the equations:
-2x + 4 = x - 5
Now, we can solve for x:
-2x - x = -5 - 4
-3x = -9
x = (-9) / (-3)
x = 3
Substituting the value of x back into Equation 2, we can solve for y:
y = 3 - 5
y = -2
What is the surface area of the cone?

Answers
Answer:
V=1/3*pi*radius(to the power of two)*height
Answer: 14 in squared
what is the difference between ANOVA and Z-test Hypothesis
Answers
The difference between ANOVA and Z-test Hypothesis is the Z-test is employed to contrast the averages of single or dual populations, whereas ANOVA is utilized for assessing the means across three or more clusters.
How to determine the differenceThe Z-test becomes possible in the comparison of the mean of a sample to that of the population. It evaluates if there is statistical relevance in the difference between the mean of a sample and the mean of the whole population
In contrast, ANOVA is employed to contrast the averages of three or more separate groups. This assesses if there is a noteworthy distinction in the averages of said groups. The F-statistic in ANOVA is computed by assessing the disparity in variability between groups and the variability within groups.
In a nutshell, the Z-test is employed to contrast the averages of single or dual populations, whereas ANOVA is utilized for assessing the means across three or more clusters.
Learn more about ANOVA at: https://brainly.com/question/25800044
#SPJ1
