Answers
Answer:
the first one
Step-by-step explanation: it is your answer because when you solve it i gt that answer i calculated it in a calculator and then showed to the teahcre and said that it was crrect please mark me as brainlist
Related Questions
In analyzing hits by certain bombs in a war, an area was partitioned into regions, each with an area of km2. A total of bombs hit the combined area of regions. Assume that we want to find the probability that a randomly selected region had exactly hits. In applying the Poisson probability distribution formula, P(x) , identify the values of , x, and . Also, briefly describe what each of those symbols represents.
Answers
Answer:
The answer is "\(\bold{ \mu =0.967, x=3, \ and \ e= 2.718}\)".
Step-by-step explanation:
A distribution of poulet applies because it deals through events (bomb hits) over even a sample space (the region with \(0.95 \ km^2\) area).
Its average hit number per area is:
\(\to \mu = \frac{\text{Number of hits of bomb}}{ \text{number of regions number}}\)
\(=\frac{535}{553} \\\\= 0.967 \\\\\)
\(\to x = 3\\\\\to e = 2.718\)
Non Shaded Shaded
Area
Area
8
Find the radius
of the small circle

Answers
Answer:
The answer is 16pi or 50.3cm² to 1 d.p
Step-by-step explanation:
The non shaded=area of shaded
d=8
r=d/2=4
A=pir³
A=p1×4²
A=pi×16
A=16picm² or 50.3cm² to 1d.p
Answer:
3.45 cm (3 s.f.)
Step-by-step explanation:
We have been given a 5-sided regular polygon inside a circumcircle. A circumcircle is a circle that passes through all the vertices of a given polygon. Therefore, the radius of the circumcircle is also the radius of the polygon.
To find the radius of a regular polygon given its side length, we can use this formula:
\(\boxed{\begin{minipage}{6 cm}\underline{Radius of a regular polygon}\\\\$r=\dfrac{s}{2\sin\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
Substitute the given side length, s = 8 cm, and the number of sides of the polygon, n = 5, into the radius formula to find an expression for the radius of the polygon (and circumcircle):
\(\begin{aligned}\implies r&=\dfrac{8}{2\sin\left(\dfrac{180^{\circ}}{5}\right)}\\\\ &=\dfrac{4}{\sin\left(36^{\circ}\right)}\\\\ \end{aligned}\)
The formulas for the area of a regular polygon and the area of a circle given their radii are:
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{nr^2\sin\left(\dfrac{360^{\circ}}{n}\right)}{2}$\\\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a circle}\\\\$A=\pi r^2$\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
Therefore, the area of the regular pentagon is:
\(\begin{aligned}\textsf{Area of polygon}&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(\dfrac{360^{\circ}}{5}\right)}{2}\\\\&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(72^{\circ}\right)}{2}\\\\&=\dfrac{\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}}{2}\\\\&=\dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}\\\\&=110.110553...\; \sf cm^2\end{aligned}\)
The area of the circumcircle is:
\(\begin{aligned}\textsf{Area of circumcircle}&=\pi \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\\\\&=\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\&=145.489779...\; \sf cm^2\end{aligned}\)
The area of the shaded area is the area of the circumcircle less the area of the regular pentagon plus the area of the small central circle.
The area of the unshaded area is the area of the regular pentagon less the area of the small central circle.
Given the shaded area is equal to the unshaded area:
\(\begin{aligned}\textsf{Shaded area}&=\textsf{Unshaded area}\\\\\sf Area_{circumcircle}-Area_{polygon}+Area_{circle}&=\sf Area_{polygon}-Area_{circle}\\\\\sf 2\cdot Area_{circle}&=\sf 2\cdot Area_{polygon}-Area_{circumcircle}\\\\2\pi r^2&=2 \cdot \dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\\end{aligned}\)
\(\begin{aligned}2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)-16\pi}{\sin^2\left(36^{\circ}\right)}\\\\r^2&=\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}\\\\r&=\sqrt{\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}}\\\\r&=3.44874763...\sf cm\end{aligned}\)
Therefore, the radius of the small circle is 3.45 cm (3 s.f.).

What is the length of QR?
600
20
Q
R
Select the best answer from the choices provided.

Answers
Answer:
A. 10 HOPE IT WILL HELP YOU
6 -9x = 5x -10x + 2 solve for x

Answers
+9. +9 -2
4 = 4x
X=1
A florist sells flower bouquets. The table shows the prices for various amounts and kinds of bouquets.
Flower Bouquets
Tole Price
daisies
$23.90
tulips
$60.80
roses
?
A customer buys 3 bouquets of tulips and 2 bouquets of roses for $147.70. What is the price of a bouquet of roses?
$28.25
$29.54
$55.93
S86.90

Answers
Answer:
$28.25
Step-by-step explanation:
$28.25
A bike company charges a rental fee plus S12 per hour. The cost for a 5-hour rental is $74.
What is the initial value?
Answers
Toni is 30 inches less than twice Jordan's height. Toni is 66 inches tall. How tall is Jordan?
Answers
Answer:
96 inches
Step-by-step explanation:
66 + 30 = 96
Suppose the average driving distance for last year's Player's Champion Golf Tournament in Ponte Vedra, FL, was 292.5 yards with a standard deviation of 14.2 yards. A random sample of 60 drives was selected from a total of 4,244 drives that were hit during this tournament. What is the probability that the sample average was 289 yards or less?
Answers
Answer:
The Probability that the sample average was 289 yards or less
P(x⁻≤ 289) = P( Z≤ -1.909) = 0.0287
Step-by-step explanation:
step(i):-
Mean of the Population = 292.5 yards
Standard deviation of the Population = 14.2 yards
sample size 'n' =60 drives
N = 4244 drives
Step(ii):-
Let X⁻ be random sample average
\(Z = \frac{x^{-} -mean}{\frac{S.D}{\sqrt{n} } }\)
Let X⁻ = 289
\(Z = \frac{289 -292.5}{\frac{14,2}{\sqrt{60} } }\)
Z = - 1.909
The Probability that the sample average was 289 yards or less
P(x⁻≤ 289) = P( Z≤ -1.909)
= 0.5 -A(1.909)
= 0.5 -0.4713
= 0.0287
Conclusion:-
The Probability that the sample average was 289 yards or less = 0.0287
Kylie makes $8.50 an hour at a local restaurant. Her paycheck shows she worked 20.88 hours last week. how much money did Kylie make?
Answers
If Kylie's hourly wage at a nearby restaurant is $8.50. She worked 20.88 hours last week, according to her paycheck. Kylie's salary is $177.48.
What is an arithmetic operation?It is defined as the operation in which we do the addition of numbers, subtraction, multiplication, and division. It has basic four operators that are +, -, ×, and ÷.
It is given that, Kylie makes $8.50 an hour at a local restaurant. Her paycheck shows she worked 20.88 hours last week.
We have to find the money did Kylie make,
We can utilize multiplication for a number of common tasks, such as figuring out how much it will cost to buy several identical things, calculating sales tax, and figuring out area and other geometric measurements.
Suppose the money did Kylie make is x,
x = 8.50 × 20.88
x=$ 177.48
Thus, if Kylie's hourly wage at a nearby restaurant is $8.50. She worked 20.88 hours last week, according to her paycheck. Kylie's salary is $177.48.
Learn more about the arithmetic operation here:
brainly.com/question/20595275
#SPJ1
distributive property of 5x 15 circle the example that correctly shows how to use the distributive property
(5×10) + (5× 5)
(5×10) x (5 x 5)
(5x10) x (5 ×15)
(5×10) + (5×15)
Answers
Answer:
The last one is correct
Step-by-step explanation:
Answer:
I think that the last one is correct
Find the area of the composite figure below and round your answer to the nearest hundredths. 3 ft 3ft
Answers
Answer:
Question
find the volume of the composite figure. round your answer to the nearest hundredth
611.08
Step-by-step explanation:
Barry and Jess are going to the fair. Barry has $25 to spend. Jess has
7/10 the amount of money Barry has. How much money Jess have to
spend at the fair?
Answers
Answer:
Step-by-step explanation:
First, Multiply 25 dollars by 7/10 and you get your answer. Then, you simplify it and then you get your answer!
Which expression is equivalent to the given polynomial expression?
(-4a2 – 36) + (-2ab – a2 + 2) + (-82 + 6ab)
OA. -3a2 + 4ab + 36
OB. -3a2 + 252 + 8ab + 36
O C. -5a2 + 4ab
36
OD -5a2 + 252 + 8ab + 36
Answers
Answer:
The equivalent expression is: \(-5a^2 + 4ab + 116\)
Step-by-step explanation:
An equivalent expression to the one given can be found removing first from the parenthesis, and then combining the like terms. So
\((-4a^2 - 36) + (-2ab - a^2 + 2) + (-82 + 6ab)\)
Removing from the parenthesis
\(-4a^2 - 36 - 2ab - a^2 + 2 - 82 + 6ab\)
Combining the like terms:
\(-4a^2 - a^2 - 2ab + 6ab - 36 + 2 - 82\)
\(-5a^2 + 4ab + 116\)
The equivalent expression is: \(-5a^2 + 4ab + 116\)
If f(x) = x2 -1 and g(x) = x- 1, what is the value of (f/g)(x)
Answers
ANSWER:
f(x) = x²-1
g(x) = x-1
f/g (x)=
x²-1÷x-1 = x-1
Ms. Monroe plays video games for 9 hours a week. A kitten plays video games for 2/3 as much LESS time. How long does the kitten play video games?
Answers
Given in the question that ;
She plays video games = 9 hours per week
The kitten plays video games = 2/3 as much less time per week
To get the hours the kitten plays the video games, find 2/3 of the time she plays video games as;
2/3 * 9 = 6 hours
So, the kitten plays video games for 6 hours as much less time compared to her
To get the hours the kitten plays video games, perform subtraction as:
9 - 6 = 3 hours
Answer
3 hours
length 21cm area 315cm2 find the breath
Answers
Answer:
Breadth = 15 cm
Step-by-step explanation:
Area = length x breadth
315 = 21 x breadth
\(\frac{315}{21} = \frac{21}{21} \times breadth\) [ dividing both sides by 21 ]
\(15 = 1 \times breadth\\\\breadth = 15 \ cm\)
___________________________________
Symbols of:\(\quad\quad\quad\quad\tt{A = A rea}\)
\(\quad\quad\quad\quad\tt{ l = length} \)
\(\quad\quad\quad\quad\tt{ b \: = breadth} \)
Given that:\(\quad\quad\quad\quad\tt{A = 315 {cm}^{2} }\)
\(\quad\quad\quad\quad\tt{l = 21cm}\)
\(\quad\quad\quad\quad\tt{b = \: ? }\)
Formula for breadth (b):\(\quad\quad\quad\quad\tt{breadth = \frac{Area}{length} }\)
Solution:\(\quad\quad\quad\quad\tt{b = \frac{315 {cm}^{2} }{21cm} }\)
\(\quad\quad\quad\tt{\:\:b = {15cm}}\)So, the breadth (b) is:\(\quad\quad\quad\quad\tt \boxed{ \boxed{ \color{magenta}{b = 15cm }}}\)
___________________________________
#CarryOnLearning
✍︎ C.Rose❀

The solution to the exponential equation below has the following general form:t=(logsubb(d/a))divided by c3 x 2^t = 12The question set has four parts. Answer the parts in order:Part 1Substituting the values below into the general form will solve the equation. Whcih value should substitute for a?a) 1b)2c)3d)12Part 2Which value should substitute for b?a) 1b) 2c) 3d) 12Part 3Which value should substitute for c?a) 1b) 2c) 3d) 12Part 4Which value should substitute for d?a) 1b) 2c) 3d) 12

Answers
From the problem, we have the equation :
\(3\cdot2^t=12\)Divide both sides by 3 :
\(2^t=\frac{12}{3}\)Take the logarithm of both sides :
\(\log 2^t=\log \frac{12}{3}\)Note that :
\(\log m^p=p\log m^{}\)the exponent can be multiplied by the logarithm of m.
So the equation will be :
\(\begin{gathered} \log 2^t=\log \frac{12}{3} \\ t\log 2=\log \frac{12}{3} \end{gathered}\)Divide both sides by log 2 so that the left side will only have the variable t.
\(t=\frac{\log(\frac{12}{3})}{\log2}\)Note that :
\(\frac{\log b}{\log a}=\log _ab\)The log of b divided by the log of a is the same as log of b with the base a.
So the equation will be :
\(\begin{gathered} t=\frac{\log(\frac{12}{3})}{\log2} \\ t=\log _2(\frac{12}{3}) \end{gathered}\)From the problem, it is in the form :
\(t=\frac{\log _b(\frac{d}{a})}{c}=\frac{\log _2(\frac{12}{3})}{1}\)So we can say that :
a = 3, b = 2, c = 1 and d = 12
Answers :
Part 1 : c. 3
Part 2 : b. 2
Part 3 : a. 1
Part 4 : d. 12
b) How many times would you expect the
spinner to land on a shaded section if it were
spun 40 times?

Answers
The number of times the spinner lands on a shaded section are 8 times.
What is the probability?
Probability is the branch of mathematics concerned with numerical descriptions of the likelihood of an event occurring or of a proposition being true.
We have,
2 Shaded sections are on a spinner,
8 unshaded sections are on a spinner,
10 total sections are on a spinner,
Therefore,
The probability of the spinner to land on a shaded section:
P = 2 ÷ 10 = 1 ÷ 5
consider x, the number of times the spinner lands on a shaded section.
If the spinner were spun 40 times:
so, \(\frac{x}{40} = \frac{1}{5}\)
By cross multiplying we get,
5x = 40
x = 8
Hence, the number of times the spinner lands on a shaded section are 8 times.
To learn more about the probability visit,
https://brainly.com/question/13604758
#SPJ1
what is the value of the expression 4 2/5(-2.5)
Answers
Answer:
-0.64
Step-by-step explanation:
Given:
4[2/5(-2.5)]
Find:
Value
Computation:
⇒ 4[2/5(-2.5)]
⇒ 8 / [-12.5]
⇒ -0.64
Seth is using the figure shown below to prove Pythagorean Theorem using triangle similarity:
In the given triangle ABC, angle A is 90° and segment AD is perpendicular to segment BC.
The figure shows triangle ABC with right angle at A and segment AD. Point D is on side BC.
Which of these could be a step to prove that BC2 = AB2 + AC2?
possible answers -
By the cross product property, AB2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by AD.
By the cross product property, AB2 = BC multiplied by AD.

Answers
The correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
To prove that \(BC^2 = AB^2 + AC^2\), we can use the triangle similarity and the Pythagorean theorem. Here's a step-by-step explanation:
Given triangle ABC with right angle at A and segment AD perpendicular to segment BC.
By triangle similarity, triangle ABD is similar to triangle ABC. This is because angle A is common, and angle BDA is a right angle (as AD is perpendicular to BC).
Using the proportionality of similar triangles, we can write the following ratio:
\($\frac{AB}{BC} = \frac{AD}{AB}$\)
Cross-multiplying, we get:
\($AB^2 = BC \cdot AD$\)
Similarly, using triangle similarity, triangle ACD is also similar to triangle ABC. This gives us:
\($\frac{AC}{BC} = \frac{AD}{AC}$\)
Cross-multiplying, we have:
\($AC^2 = BC \cdot AD$\)
Now, we can substitute the derived expressions into the original equation:
\($BC^2 = AB^2 + AC^2$\\$BC^2 = (BC \cdot AD) + (BC \cdot AD)$\\$BC^2 = 2 \cdot BC \cdot AD$\)
It was made possible by cross-product property.
Therefore, the correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
For more questions on cross-product property:
https://brainly.com/question/14542172
#SPJ8
pls help pls ill mark brainliest
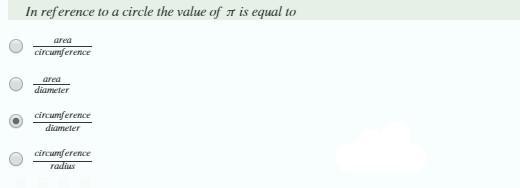
Answers
Answer:
Area/Circumference is the length of a circle!
Step-by-step explanation:
Answer: the answer is area/ circumference
Step-by-step explanation:
Please help me please please help ASAP

Answers
Step-by-step explanation:
70 + 45 = 115
180 - 115 = 65
angle c = 65
use sohcahtoa
cos angle = adjacent
hypotenuse
cos 65 = 2.5
b
b cos 65 = 2.5
use the calc for further answers
hope that helped


Expand and combine like terms.
(2x3 + 4x5)2 =
Answers
Answer:
52
Step-by-step explanation:
(2x3 = 6
4x5 = 20)
(6+20) = (26)
(26)2 = 52
=52
What would the phrase "three times the sum of a number and 4" look like as a
variable expression?
3x +4
O3(3x +4)
O3(x + 4)
3x -4
Answers
Which of the following is Playfair's axiom?
A. A straight line segment can be drawn between any two points.
B. A circle can be drawn with any center and radius.
C. Through a given point not on a given line, there is exactly one line
parallel to the given line.
D. All right angles are equal to one another.
Answers
Answer:
C. Through a given point not on a given line, there is exactly one line parallel to the given line.
Step-by-step explanation:
hope i helped
Answer:
Look down
Step-by-step explanation:
Thanks for reaching out for assistance! Based on the context you provided, it seems like the correct answer is C. Playfair's axiom states that there is exactly one line parallel to a given line that can be drawn through a point not on it. I hope this helps! Let me know if there's anything else I can do for you.
a floor plan is drawn using a scale of 3cm/15ft what length is represented by 1 centimeter ?
Answers
Answer:
1cm= 5ft.
Step-by-step explanation:
divide 15 by three
I need help with these pages, please help me !


Answers
Answer:
the answer is 2
Step-by-step explanation:
2
The population, in millions of people, of the United States can be represented by the recursive
formula below, where a represents the population in 1910 and n represents the number of years
since 1910.
ao
an 1.015a, - 1
Identify the percentage of the annual rate of growth from the equation a,, = 1.015a, - 1
= 92.2
=
Write an exponential function, P, where P(t) represents the United States population in millions
of people, and t is the number of years since 1910.
According to this model, determine algebraically the number of years it takes for the population of
the United States to be approximately 300 million people. Round your answer to the nearest year.

Answers
53 years for the Population of the United States to reach 300 million people according to this model.
The recursive formula of the population of the United States is given by ao = an1.015a - 1
Let's solve this to get a formula that is not recursive.a0 = a0 givena1 = 1.015a0 - 1a2 = 1.015a1 - 1 = 1.015 (1.015a0 - 1) - 1 = 1.0152 a0 - 1.015 - 1a3 = 1.015a2 - 1 = 1.015(1.015²a0 - 1.015 - 1) - 1 = 1.015³ a0 - 1.015² - 1.015 - 1a4 = 1.015a3 - 1 = 1.015(1.015³a0 - 1.015² - 1.015 - 1) - 1 = 1.015⁴ a0 - 1.015³ - 1.015² - 1.015 - 1an = 1.015na0 - 1.015n-1 - 1.015n-2 - ... - 1.015 - 1We can rewrite this asan = a0(1.015)
where a0 is the population of the United States in 1910 (92.2 million people) .
Now, we need to write an exponential function to find the population of the United States as a function of time in years since 1910.P(t) = 92.2(1.015)
To find the number of years it takes for the population to reach 300 million people, we need to solve the equation92.2(1.015)t = 300
Dividing both sides by 92.2, we get1.015t = 3.2596
Taking the natural logarithm of both sides, we get ln(1.015) = ln(3.2596)t = ln(3.2596)/ln(1.015) ≈ 53.2
Therefore, approximately 53 years for the population of the United States to reach 300 million people according to this model.
For more questions on Population .
https://brainly.com/question/30412211
#SPJ8
There are five roses in a vase of 14 flowers. The rest are daisies.
(a) what is the ratio of all flowers in the vase daisies?
(B) What is the ratio of daisies to roses?
Answers
The required solution is as follows,
(a) The ratio of all flowers in the vase daisies is 14: 9
(b) The ratio of daisies to roses 9:5
The ratio can be defined as the comparison of the fraction of one quantity towards others. e.g.- water in milk.
Here,
Number of daises in vase = 14 - 5 = 9
(a) The ratio of all flowers in the vase daisies,
= 14 / 9 or 14:9
(a) The ratio of daisies to roses,
= 9 / 5 or 9 : 5
Thus, the required ratio of flowers is given above.
Learn more about Ratio here:
brainly.com/question/13419413
#SPJ1
Anthony surveys a group of students at his school about whether they play a
sport. This table shows the results broken down by gender.
Boys
Girls
Total
Play a sport
95
76
171
Do not play a
sport
45
59
104
A. Yes, they are independent, because P(girl)
a sport) ~0.62
Are being a girl and playing a sport independent events? Why or why not?
B. Yes, they are independent, because P(girl)
a sport) -0.44
Total
C. No, they are not independent, because P(girl) 0.49 and
P(girl plays a sport) ~ 0.62.
140
135
275
0.49 and Pigirl | plays
0.49 and P(girl plays
D. No, they are not independent, because P(girl)-0.49 and
Pigirl plays a sport)~0.44.
Answers
Being a girl and playing a sport are C. No, they are not independent events, because P(girl) 0.49 and P(girl plays a sport) ~ 0.62.
Let's consider the probabilities:
P(girl) = (number of girls) / (total number of students) = 135 / 275 ≈ 0.49
P(girl plays a sport) = (number of girls playing a sport) / (total number of students) = 76 / 275 ≈ 0.276
If being a girl and playing a sport were independent events, the joint probability would be the product of the individual probabilities:
P(girl) × P(girl plays a sport) ≈ 0.49 × 0.276 ≈ 0.13524
However, the actual joint probability is different from the expected value:
P(girl, plays a sport) ≈ 76 / 275 ≈ 0.276
Since the joint probability does not match the product of the individual probabilities, we can conclude that being a girl and playing a sport are not independent events based on the given data.
Therefore, option C. No, they are not independent, because P(girl) 0.49 and P(girl plays a sport) ~ 0.62. is the correct answer.
For more questions on events
https://brainly.com/question/29782219
#SPJ8
