QUESTIONS: SOLVE FOR X
please help if you can !
please don't comment just to comment if its not gonna help me i really need help.

Answers
Related Questions
8.
Find the equation to the line passing through the point of intersection of the lines
3x + 14 =
2y and x + y = 6, and is also perpendicular to the line 5x =
6y + 1.
Answers
9514 1404 393
Answer:
30x +25y = 148
Step-by-step explanation:
We can use substitution to find the point of intersection of ...
3x +14 = 2yx + y = 6Using the second equation, we can write an expression for y:
y = 6 -x
Substituting that into the first equation gives ...
3x +14 = 2(6 -x)
3x +14 = 12 -2x . . . . . eliminate parentheses
5x = -2 . . . . . . . . . . . add 2x-14
x = -0.4 . . . . . . . . . divide by 5
y = 6 -(-0.4) = 6.4
__
Now, we want an equation for a line through the point (-0.4, 6.4) that is perpendicular to 5x = 6y+1
The perpendicular line will have the coefficients swapped with one of them negated. The constant will accommodate the given point.
6x = -5y + c
6(-0.4) +5(6.4) = c = 29.6
The perpendicular line can be written ...
6x = -5y +29.6
In standard form, the equation is ...
30x +25y = 148

he highest elevation in a country is a mountain, with an altitude of 14,309feet. The lowest elevation in the country is a valley, with an altitude of 288 feet below sea level.
Answers
Answer:
Diffrent between altitude = 14,021 ft
Step-by-step explanation:
Given:
Heighest altitude = 14,309 ft
Lowest altitude = 288 ft
Find:
Diffrent between altitude
Computation:
Diffrent between altitude = Heighest altitude - Lowest altitude
Diffrent between altitude = 14,309 - 288
Diffrent between altitude = 14,021 ft
Which of the following terms best describes the relationship between /W and /X ( Answer as soon as possible please)

Answers
Answer:
B. Same-side interior angles
Step-by-step explanation:
Angle w and angle x lie on the same side of the transversal that cut across the two parallel lines, and are also within the two parallel lines. They are therefore regarded as same-side interior angles. Same-side interior angles are supplementary.
Which table represents exponential growth? A 2-column table has 4 rows. The first column is labeled x with entries 1, 2, 3, 4. The second column is labeled y with entries 2, 4, 6, 8. A 2-column table has 4 rows. The first column is labeled x with entries 1, 2, 3, 4. The second column is labeled y with entries 2, 4, 8, 16. A 2-column table has 4 rows. The first column is labeled x with entries 1, 2, 3, 4. The second column is labeled y with entries 2, 4, 7, 11. A 2-column table has 4 rows. The first column is labeled x with entries 1, 2, 3, 4. The second column is labeled y with entries 2, 4, 6, 10. HELP ME IMMEDIATELY!
Answers
The table that represents exponential growth is the second table.. The second column is labeled y with entries 2, 4, 6, 8. A 2-column table has 4 rows.
What is exponential growth?Exponential growth simply means a process that increases quantity over time. It occurs when the instantaneous rate of change of a quantity with respect to time is proportional to the quantity itself.
Exponential growth is the pattern of data which shows sharper increases over time. In finance, compounding creates exponential returns and the savings accounts with a compounding interest rate can show exponential growth.
In this case, the second table described represents an exponential function. It has a common ratio of 4, meaning that each y-value is multiplied by 4 to get to the next value. Here, every time the X's increase by 1, the Ys increase by a multiple of 4.
One of the best examples of exponential growth is observed in bacteria. Here, it takes bacteria roughly an hour to reproduce through prokaryotic fission. This illustrates exponential growth.
Learn more about exponential growth on:
brainly.com/question/4172151
What are the solutions to the following equation?
Answers
Answer:
What equation?
Step-by-step explanation:
Cual es la distancia que recorrió luis en su bicicleta rodada 20p (2.54) después que las llantas dieran 50 vueltas completas
porfaaa
Answers
Luis traveled approximately 31,736.8 inches on his bicycle.
We have,
To find the distance that Luis traveled on his bicycle, we need to calculate the circumference of the tires and then multiply it by the number of complete turns.
Given:
Radius of the tires (r) = 20p (2.54) inches
Number of complete turns (n) = 50
The circumference of a circle can be calculated using the formula:
Circumference = 2πr
Substituting the given radius into the formula, we have:
Circumference = 2π * (20p) inches
Now we can calculate the distance traveled (d):
Distance = Circumference x Number of complete turns
Distance = 2π x (20p) x 50 inches
To simplify the calculation, we can approximate π as 3.14:
Distance ≈ 2 x 3.14 x (20 x 2.54) x 50 inches
Calculating this expression, we find:
Distance ≈ 31736.8 inches
Therefore,
Luis traveled approximately 31,736.8 inches on his bicycle.
Learn more about Circle here:
https://brainly.com/question/11833983
#SPJ1
The complete question.
What is the distance that Luis traveled on his bicycle rolled 20p (2.54) after the tires gave 50 complete turns
Point A has coordinates (3,4). After a translation 4 units left, a reflection across the x-axis, and a translation 2 units down, what are the coordinates of the image? Write your coordinates with a comma and no spaces inside parenthesis, for example (1,2).
Answers
If a point, (x, y) is translated c units to the left, the new coordinate would be
(x - c, y)
Given that point A with coordinates, (3, 4) is translated 4 units left, the new coordinate would be
(3 - 4, 4)
= (- 1, 4)
If a point, (x, y) is reflected across the x-axis, the sign of the x coordinate remains unchanged while the sign of the y coordinate would change. This gives us (x, - y). Thus, if (- 1, 4) is reflected across the x-axis, the new point would be
(- 1, - 4)
If a point, (x, y) is translated c units down, the new point would be (x, y - c)
Thus, if (- 1, - 4) is translated 2 units down, the new point would be (- 1, - 4 - 2)
= (- 1, - 6)
The final coordinate is
(- 1, - 6)
Annette has 3 hours to spend training for an upcoming race. She completes her training by running full speed the distance of the race and walking back the same distance to cool down. If she runs at a speed of 9mph and walks back at a speed of 3mph , how long should she plan to spend walking back?
Answers
Answer:
Annette should plan to spend 2.25 hours walking back.
Step-by-step explanation:
To solve this problem, we can use the formula:
Time = Distance / Speed
Let's assume the distance of the race is D miles.
Annette spends her time running the distance of the race, which takes:
Time running = D / 9 hours
She then walks back the same distance, which we need to find the time for:
Time walking = D / 3 hours
Since Annette has a total of 3 hours for her training, the sum of the running time and walking time should equal 3 hours:
D / 9 + D / 3 = 3
To simplify the equation, we can multiply all terms by 9 to eliminate the denominators:
D + 3D = 27
Combining like terms:
4D = 27
Dividing both sides of the equation by 4:
D = 6.75
So, the distance of the race is 6.75 miles.
To find the time Annette should spend walking back, we substitute the distance into the time-walking formula:
Time walking = D / 3 = 6.75 / 3 = 2.25 hours
Therefore, Annette should plan to spend 2.25 hours walking back.
Your friend likes to show off to his coworkers using statistical terminology, but he makes errors so much that you often have to correct him. He just completed the following hypothesis test: H0 : μ = 100 ; HA : μ ≠ 100 x = 105, s = 10, n = 40 p-value = 0.0016 He claims the definition of this p-value is "the probability of obtaining a sample mean of 105 from a random sample of n = 40 when the true population mean is assumed to be 100." Which of the following is true?
a. Your friend is wrong, the sample size is irrelevant.
b. Your friend is right.
c. Your friend is wrong, the statement should be revised as "the probability of obtaining a sample mean of 105 from a random sample of n = 40 when the true population mean is assumed to be different than 105."
d. Your friend is wrong, the statement should be revised as "the probability of obtaining a sample mean of 105 or more extreme from a random sample of n = 40 when the true population mean is assumed to be 100."
Answers
Answer:
Option d: Your friend is wrong, the statement should be revised as "the probability of obtaining a sample mean of 105 or more extreme from a random sample of n = 40 when the true population mean is assumed to be 100."
Step-by-step explanation:
We are given;
Null hypothesis; H0 : μ = 100
Alternative hypothesis; HA : μ ≠ 100
Sample mean; x = 105
Sample standard deviation; s = 10
Sample size; n = 40
p - value = 0.0016
Looking at the options, the first option is wrong because the sample size is not irrelevant her since it's more than 30.
The second option can't be correct because they just told us he is right without giving explanation.
The third option is wrong because 100 is the true population mean and not 150.
Thus we are left with Option D as the correct answer.
Could someone please help here in so lost

Answers
Answer:
x=3
(26x+50degreese) = 134 degreese
Step-by-step explanation:
Mifflin Paper Company just upgraded to a heavier cardstock paper for its $42.00
business cards. To compensate for the increase in quality, Mifflin Paper Company is
raising its prices by 19%. What is the new price of business cards?
Answers
Answer:
49.98
Step-by-step explanation:
expression: the product of 4 and n.
A. 4/n
B. 4 + n
C. 4 – n
D. 4n
Answers
Answer:
D
product of 4 and n is the same as 4× n
and it is equal to 4n
Find the slope of the tangent line to the curve defined by 4x2+5xy+y4=370
at the point (−9,−1)
Answers
Answer:
The slope of the tangent line to the curve at the given point is -11/7.
Step-by-step explanation:
Differentiation is an algebraic process that finds the gradient (slope) of a curve. At a point, the gradient of a curve is the same as the gradient of the tangent line to the curve at that point.
Given function:
\(4x^2+5xy+y^4=370\)
To differentiate an equation that contains a mixture of x and y terms, use implicit differentiation.
Begin by placing d/dx in front of each term of the equation:
\(\dfrac{\text{d}}{\text{d}x}4x^2+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=\dfrac{\text{d}}{\text{d}x}370\)
Differentiate the terms in x only (and constant terms):
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=0\)
Use the chain rule to differentiate terms in y only. In practice, this means differentiate with respect to y, and place dy/dx at the end:
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Use the product rule to differentiate terms in both x and y.
\(\boxed{\dfrac{\text{d}}{\text{d}x}u(x)v(y)=u(x)\dfrac{\text{d}}{\text{d}x}v(y)+v(y)\dfrac{\text{d}}{\text{d}x}u(x)}\)
\(\implies 8x+\left(5x\dfrac{\text{d}}{\text{d}x}y+y\dfrac{\text{d}}{\text{d}x}5x\right)+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
\(\implies 8x+5x\dfrac{\text{d}y}{\text{d}x}+5y+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Rearrange the resulting equation in x, y and dy/dx to make dy/dx the subject:
\(\implies 5x\dfrac{\text{d}y}{\text{d}x}+4y^3\dfrac{\text{d}y}{\text{d}x}=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}(5x+4y^3)=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8x-5y}{5x+4y^3}\)
To find the slope of the tangent line at the point (-9, -1), substitute x = -9 and y = -1 into the differentiated equation:
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8(-9)-5(-1)}{5(-9)+4(-1)^3}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{72+5}{-45-4}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{77}{49}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{11}{7}\)
Therefore, slope of the tangent line to the curve at the given point is -11/7.
Coliform bacteria are distributed in a river at an average concentration of 1 per 20 cc of water. If we draw from the river a test tube containing 10cc of water, what is the probability that the sample contains exactly 2 coliform bacteria
Answers
Answer:
0.5
Step-by-step explanation:
Given that: An average concentration of 1 coliform bacteria per 20 cc of the river water.
This implies that in 20 cc of the water, it is certain that 1 coliform bacteria would be found. So that:
pr(1 bacteria in 20 cc of water) = 1
i.e the probability of getting 1 bacteria in 20 cc of water is 1.
The probability of the 10 cc sample of water containing 2 coliform bacteria can be determined as:
pr(2 bacteria in 10 cc of water) = \(\frac{1}{2}\)
= 0.5
The table shows the monthly rainfall at a measuring station. What is the mean monthly rainfall? Round your answer to the nearest thousandth.
Answers
The mean monthly rainfall, Rounded to the nearest thousandth, is 2.520 inches.
To determine the mean monthly rainfall, we need to calculate the average of the rainfall values provided in the table. Here is the table:
| Month | Rainfall (in inches) |
|-------|----------------|
| January | 2.3
| February | 1.7
| March | 3.2
| April | 2.9
| May | 2.5
To find the mean monthly rainfall, we add up the rainfall values for each month and divide the sum by the total number of months. In this case, we have five months:
Mean Monthly Rainfall = (2.3 + 1.7 + 3.2 + 2.9 + 2.5) / 5
Calculating the sum of the rainfall values:
Mean Monthly Rainfall = 12.6 / 5
Dividing the sum by the number of months:
Mean Monthly Rainfall = 2.52
Rounded the result to the nearest thousandth, the mean monthly rainfall is approximately 2.520 inches.
Therefore, the mean monthly rainfall, rounded to the nearest thousandth, is 2.520 inches.
To know more about Rounded .
https://brainly.com/question/30545728
#SPJ8
number of bald eagles in a country a discrete random variable, a continuous random variable, or not a random variable?
Answers
Answer:
Discrete random variable.
Step-by-step explanation:
Discrete variable:
Countable numbers(0,1,2,3,...)
Continuous variable:
Can assume decimal values, such as 0.5, 2.5,...
Number of bald eagles:
Number of bald eagles is a countable value, either there a 0, 100, 1000,... so it is a discrete random variable.
Answer:
Discrete random variable.
Step-by-step explanation:
I will give brainliest!

Answers
Answer: Its B
Step-by-step explanation:
Suppose the life time (in hours) of a battery brand is normally distributed. A random sample of 16 batteries results in a sample variance of
3.25
hours
2
. We want to test if there is significant/sufficient evidence in the sample data to claim that the variance of the battery life population is different than 4 hours
2
at significance level of
0.05
. Which of the following is INCORRECT? A.
H 0
:σ 2
=4 vs H 1
:σ 2
=4
B. The test statistic is found to be
12.1875
C. We should reject the null hypothesis and there is sufficient evidence to claim that the variance of battery life is different than 4 hours
2
at significance level of
0.05
. D. None of the above.
Answers
there is not sufficient evidence to claim that the variance of the battery life population is different than 4 hours2 at a significance level of 0.05.
answer is D. None of the above.
To test if there is significant evidence to claim that the variance of the battery life population is different than 4 hours2, we can use a chi-square test.This is how the test statistic is computed:
X2 = (n-1)*(s2/σ2)
where n is the sample size, s2 is the sample variance and σ2 is the population variance.
In this case, n = 16, s2 = 3.25 and σ2 = 4
X2 = (16-1)*(3.25/4) = 12.1875
The critical value of X2 with 15 degrees of freedom and α = 0.05 is 24.996. Therefore, since 12.1875 < 24.996, we fail to reject the null hypothesis, and there is not sufficient evidence to claim that the variance of the battery life population is different than 4 hours2 at a significance level of 0.05.
Learn more about variance here
https://brainly.com/question/13708253
#SPJ4
10. Based on the diagram below, which statement is true?

Answers
Answer:
Part D is correct
Step-by-step explanation:
What is the equation of the line that passes through the point (-4,1) and has a slope of -5/4
Answers
Answer:
y = -5/4x -4
Step-by-step explanation:
slope(m)= -5/4
x1=-4,y1=1
using the formula for one point form
y-y1=m(x-x1)
y-1= -5/4(x-(-4))
y-1 = -5/4x + -5/4 × +4
y - 1 = -5/4x -5
y=-5/4x -5 + 1
y = -5/4x -4.
Don't forget to smash the answer as brainliest if I truly deserve it
Thanks
-b-
Note: Figure is not drawn to scale.
If a = 5m, b = 8 m, c = 8 m, and d = 2 m, what is the perimeter of the swimming pool?
OA.
21 m
OB.
32 m
29 m
34 m
OC.
OD.
6 of 10 Answered
Reset
Submit
Session Timer: 78:05
O Search
C
Answers
After considering the given data we conclude that the perimeter of the given swimming pool is 23 meters which is Option A.
The perimeter of a rectangle is evaluated by adding up all its sides. For the given case, we possess a rectangle with sides
a = 5m,
b = 8m,
c = 8m and
d = 2m.
Perimeter regarding the swimming pool is evaluated as
a + b + c + d
= 5m + 8m + 8m + 2m
= 23 meters
Hence the option regarding the question which satisfy the perimeter is Option A.
Perimeter the counted measurement regarding the distance around the outside of a two-dimensional shape. In this system the length of the outline or boundary of any two-dimensional geometric shape is defined as perimeter .
To learn more about perimeter
https://brainly.com/question/19819849
#SPJ1
The complete question is
If a = 5m, b = 8 m, c = 8 m, and d = 2 m, what is the perimeter of the swimming pool?
A.23 m
B. 32 m
C.29 m
D.34 m
The girls in Lana’s troop set a goal to sell 1,000 boxes of cookies this year. There are 13 girls in the troop. At least how many boxes of cookies should each girl sell to reach their goal?
Answers
Answer:
77 boxes each
Step-by-step explanation:
1,000/13
Answer:
Step-by-step explanation:
1000/13= 76.9 .... Each girl needs to sell 77 boxes
James is making a scale model of his bedroom. The model is
0.6 feet wide. If the actual room is 17.5 times as wide as the
model, what is the width of James's room?
A 18.1 feet
(B) 17.11 feet
© 16.9 feet
D 10.5 feet
Answers
Answer:
D
Step-by-step explanation:
0.6x17.5 which is 10.5
Find the standard deviation of the sampling distribution of sample means using the given information. Round to one decimal place, if necessary. μ = 64 and o = 12; n = 9
Answers
The standard deviation of the data sample is 2.55.
What is the standard deviation of the data sample?The standard deviation of the data sample is calculated by applying the following formula;
S.D = √ (x - μ)²/(n - 1)
where;
μ is the mean of the distributionx is the sample datan is the number of sample dataThe given parameters;
mean, μ = 64
x, = 12
number of samples = 9
The standard deviation of the data sample is calculated as;
S.D = √ (12 - 64)²/(9 - 1)
S.D = 2.55
Thus, the standard deviation of the data sample is calculated by applying the formula for standard deviation.
Learn more about standard deviation here: https://brainly.com/question/24298037
#SPJ1
What is the area of a sector when 0=pi/2 radians and r=8/3

Answers
\(\textit{area of a sector of a circle}\\\\ A=\cfrac{\theta r^2}{2} ~~ \begin{cases} r=radius\\ \theta =\stackrel{radians}{angle}\\[-0.5em] \hrulefill\\ \theta =\frac{\pi }{2}\\[1em] r=\frac{8}{3} \end{cases}\implies A=\cfrac{1}{2}\cdot \cfrac{\pi }{2}\cdot\left( \cfrac{8}{3} \right)^2 \\\\\\ A=\cfrac{1}{2}\cdot \cfrac{\pi }{2}\cdot \cfrac{64}{9}\implies A=\cfrac{16\pi }{9}\implies A\approx 5.59\)
Determine the probability of rolling a die and getting a 2
then a 5.
Answers
The probability of rolling a die and getting a 2, then a 5, is 1/36.
To determine the probability of rolling a die and getting a 2, then a 5, we need to multiply the probabilities of each event happening.
First, let's consider the probability of rolling a die and getting a 2. Since there are six equally likely outcomes when rolling a fair six-sided die (numbers 1 to 6), the probability of rolling a 2 is 1/6.
Now, let's consider the probability of rolling a die and getting a 5. Again, there are six equally likely outcomes, so the probability of rolling a 5 is also 1/6.
To find the probability of both events happening, we multiply the probabilities:
Probability of rolling a 2 and then a 5 = (1/6) * (1/6) = 1/36.
Therefore, the probability of rolling a die and getting a 2, then a 5, is 1/36.
It's important to note that each roll of the die is an independent event, meaning that the outcome of one roll does not affect the outcome of the next roll. Therefore, the probability of rolling a 2 and then a 5 remains constant at 1/36 regardless of previous rolls or the order in which they occur.
For more such questions on probability visit:
https://brainly.com/question/251701
#SPJ8
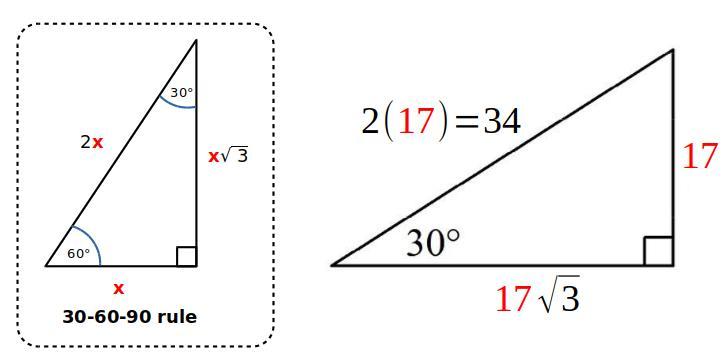
Label the triangle sides, assuming the angle of interest is the 30-degree angle:
solve for
The side with x is the
blank side.
The side with y is the
NO SPAM I WILL REPORT YOU
blank side.
The side with 17 is the blank side

Answers
Check the picture below.
Convert 3207 nine to a numeral in base ten.
Answers
3x+4
12. Simplify +
x+2
x²+2x
2x+4

Answers
Answer:
\(\dfrac{x^2+8x+8}{2x+4}\\\\\)
Step-by-step explanation:
Simplify:
\(\dfrac{3x + 4}{x +2}+\dfrac{x^2+2x}{2x+ 4}\)
Multiply the denominator and the numerator of the first term by 2,
\(=\dfrac{2*(3x +4)}{2*(x+ 2)}+\dfrac{x^2+2x}{2x+4}\\\\\\=\dfrac{2*3x+2*8}{2*x +2*2}+\dfrac{x^2+2x}{2x+4}\\\\\\=\dfrac{6x+8}{2x+4}+\dfrac{x^2+2x}{2x+4}\)
\(\sf = \dfrac{6x+8+x^2+2x}{2x+4}\\\\\text{\bf Combine like terms,}\\\\=\dfrac{x^2+8x+8}{2x+4}\\\\\)
A school is installing a flagpole in the central plaza. The plaza is a square with side length 100 yards as shown in the figure below. The flagpole will take up a square plot in the middle of the plaza and its base will have an area of x^2−6x+9 yd^2.
Area of the flagpole plot: x^2−6x+9
Find the length of the base of the flagpole by factoring. (Hint: Because the area of the flagpole is an expression that involves the variable x, the length of the base will also involve the variable x.)
The length of the base of the flagpole is
Answers
Answer:
\(x-3\)
Step-by-step explanation:
The area of the flagpole base is \(x^2-6x+9\ \text{yd}\)
where the factor of the equation is the length of the base.
In order to find the length we need to factorize the equation
\(x^2-6x+9\)
\(=x^2-3x-3x+9\)
\(=x(x-3)-3(x-3)\)
\(=(x-3)(x-3)\)
The length of the base of the flagpole is \((x-3)\ \text{yd}\).
The area of a square base is the product of the side lengths.
The length of the base is x - 3
The area is given as:
\(\mathbf{Area =x^2 - 6x + 9}\)
Expand
\(\mathbf{Area =x^2 - 3x - 3x + 9}\)
Factorize
\(\mathbf{Area =x( x- 3) - 3(x - 3)}\)
Factor out x - 3
\(\mathbf{Area =( x- 3) (x - 3)}\)
Express as squares
\(\mathbf{Area =( x- 3)^2}\)
Rewrite the area as:
\(\mathbf{Length^2 =( x- 3)^2}\)
Take square roots of both sides
\(\mathbf{Length =x- 3}\)
Hence, the length of the base is x - 3
Read more about area of squares at:
https://brainly.com/question/1658516