Sofia bought a package of 20 bottles of water. Each bottle contains w ounces. Write an
expression that shows the total number of ounces.
Answers
Answer:
20w
Step-by-step explanation:
If you have 20 bottles, and each contains w ounces, we can use the following example to solve.
If there were 4oz per bottle,
20 * 4 = 80
80oz
We have w oz per bottle,
20 * w = ?
20w
Related Questions
compatible numbers are used to estimate this sum. 181 204 which estimate is the most accurate? responses 350 350 375 375 425 425 450
Answers
The most accurate estimated sum of 181 and 204 is 380
The given numbers are 181 and 204
The compatible numbers are defined as the numbers that are easy to do the arithmetic operations. The arithmetic operations are addition, subtraction, division and multiplication etc.
To find the sum of the compatible numbers first we have to round the given numbers to the nearest tens or hundreds and do the the arithmetic operation
Round 181 to the nearest tens = 180
Round 204 to the nearest tens = 200
Then the sum of compatible numbers will be
180 + 200 = 380
Therefore, the most accurate estimation is 380
Learn more about compatible numbers here
brainly.com/question/627054
#SPJ4
a professor gives the following scores to her students. (score,frequency) [(35,1) (45,3) (55,6) (65,11) (75,13) (85,10) (95,2) what is the sample standard deviation for the data?
Answers
The sample standard deviation for the given score and frequency is equal to 8.150.
The sample standard deviation for the ,
Calculate the sample mean (X).
X = Σ(x × f) / Σf,
where x = score, f = frequency
Mean X
= (35×1 +45×3 +55×6 + 65×11 +75×13 + 85×10 + 95×2) /(1+3+6+11+13+10+2)
= 35 + 135 + 330 + 715 + 975 + 850 + 190 / 46
= 3230 /46
= 70.2
Calculate the deviation of each score from the mean (x - X).
For 35, (35 - 70.2) = -35.2
For 45, (45 - 70.2) = -25.2
For 55, (55 - 70.2) = -15.2
For 65, (65 - 70.2) = -5.2
For 75, (75 - 70.2) = 4.8
For 85,(85 - 70.2) = 14.8
For 95, (95 - 70.2) = 24.8
Square each deviation ( (x - X)² ).
For 35, (-35.2)² = 1239.04
For 45, (-25.2)²= 635.04
For 55, (-15.2)² = 231.04
For 65,(-5.2)² = 27.04
For 75,(4.8)² = 23.04
For 85, (14.8)² = 219.04
For 95, (24.8)² = 615.04
Calculate the sum of squared deviations.
Σ(x - X)²
= 1239.04 + 635.04 + 231.04 + 27.04+ 23.04 + 219.04 + 615.04
= 2989.28
Calculate the variance (s²).
s² = Σ(x - X)² / (n - 1)
⇒s² = 2989.28 / 46 -1
⇒s² =66.428
Calculate the sample standard deviation (s).
s = √(s²)
⇒s = √(66.428)
⇒ s = 8.150 (rounded to three decimal places)
Therefore, the sample standard deviation for the given data is 8.150.
Learn more about sample standard deviation here
brainly.com/question/31848111
#SPJ4
PLEASE HELP QUICK LOTS OF POINTS!

Answers
Answer:
What are the answer choices?
Step-by-step explanation:
Simplify each radical expression. 1/√4
Answers
The simplified form of 1/√4 is 1/2 or 0.5.
To simplify the radical expression 1/√4, we can start by finding the square root of 4, which is 2. So, the expression becomes 1/2.
To simplify it further, we can multiply the numerator and denominator by the conjugate of the denominator. In this case, the conjugate of 2 is also 2.
Multiplying the numerator and denominator by 2, we get (1 * 2) / (2 * 2), which simplifies to 2/4.
Finally, we can simplify the fraction 2/4 by dividing both the numerator and denominator by their greatest common divisor, which is 2.
Dividing 2 by 2 gives us 1, and dividing 4 by 2 gives us 2.
Therefore, the simplified radical expression 1/√4 is equal to 1/2, or in decimal form, 0.5.
In conclusion, the simplified form of 1/√4 is 1/2 or 0.5.
Learn more about radical expression from the given link;
https://brainly.com/question/31923084
#SPJ11
HELP WILL MARK BRAINLIEST

Answers
Answer:
Volume = 12
Step-by-step explanation:
Answer:
12cm³
Step-by-step explanation:
L=3cm
W=2cm
H=2cm
Volume=L*W*H
Volume =3*2*2
=12 cm³
I need help with this question ;w;

Answers
Answer:
XZ = 16.25 cm
QR = 6.8 cm
Step-by-step explanation:
A) Taking the proportion of similar sides
=> \(\frac{7.2}{6.5} = \frac{18}{XZ}\)
Cross Multiplying
=> 7.2 XZ = 18*6.5
=> XZ = 117/7.2
=> XZ = 16.25 cm
B) Taking proportion of similar sides
=> \(\frac{18}{17}=\frac{7.2}{QR}\)
Cross Multiplying
=> 18 QR = 17*7.2
=> QR = 122.4/18
=> QR = 6.8 cm
An expert in gardening tells Lela that she needs to mix two-thirds quart of sand with every 112 quarts of potting soil.
If she needs 52 quarts of mixture in total, how much sand should she use?
Answers
She should use 16 quarts of sand for obtaining total of 52 quarts of mixture. The solution has been obtained by using the arithmetic operations.
What are arithmetic operations?
All real numbers are believed to be explicable by the four fundamental operations, sometimes known as "arithmetic operations." Mathematics places operations such as quotient, product, sum, and difference after operations such as division, multiplication, addition, and subtraction.
We are given that with every 1\(\frac{1}{2}\) quarts of potting soil,, two-thirds quart of sand is to be mixed.
So, from this we get
Total mixture = 1\(\frac{1}{2}\) + \(\frac{2}{3}\)
Total mixture = \(\frac{13}{6}\) quarts
Now, on dividing sand and total mixture by 13, we get
\(\frac{2}{39}\) quarts of sand produces in total \(\frac{1}{6}\) quarts of mixture.
Now, on multiplying sand and total mixture by 6, we get
\(\frac{12}{39}\) quarts of sand produces in total 1 quarts of mixture.
So,
⇒ For 52 quarts of mixture = \(\frac{624}{39}\) quarts of sand
⇒ For 52 quarts of mixture = 16 quarts of sand
Hence, she should use 16 quarts of sand for obtaining total of 52 quarts of mixture.
Learn more about arithmetic operations from the given link
brainly.com/question/30283549
#SPJ1
The complete question has been attached below.

The four control points in 2D plane are Po(0,0) ?, (1, 1), P₂ (2,-1) and P3 (3,0). The tangent veehrs at the end points are Po'(1,1) & P3'(1,1). Determine the intermiclate points on the Humite curve at t = 1/3 & 2/3
Answers
The Hermite curve with four control points P0(0,0), P1(1,1), P2(2,-1), and P3(3,0) has tangent vectors P0'(1,1) and P3'(1,1) at the endpoints. To determine the intermediate points on the curve at t = 1/3 and t = 2/3, we can use the Hermite interpolation formula.
The Hermite interpolation formula allows us to construct a curve based on given control points and tangent vectors. In this case, we have four control points P0, P1, P2, and P3, and tangent vectors P0' and P3'.
To find the intermediate point at t = 1/3, we use the Hermite interpolation formula:
P(t) = \((2t^3 - 3t^2 + 1)P0 + (-2t^3 + 3t^2)P3 + (t^3 - 2t^2 + t)P0' + (t^3 - t^2)P3'\)
Substituting the given values:
\(P(1/3) = (2(1/3)^3 - 3(1/3)^2 + 1)(0,0) + (-2(1/3)^3 + 3(1/3)^2)(3,0) + ((1/3)^3 - 2(1/3)^2 + (1/3))(1,1) + ((1/3)^3 - (1/3)^2)(1,1)\)
Simplifying the equation, we can find the coordinates of the intermediate point at t = 1/3.
Similarly, for t = 2/3, we use the same formula:
\(P(2/3) = (2(2/3)^3 - 3(2/3)^2 + 1)(0,0) + (-2(2/3)^3 + 3(2/3)^2)(3,0) + ((2/3)^3 - 2(2/3)^2 + (2/3))(1,1) + ((2/3)^3 - (2/3)^2)(1,1)\)
Calculating the equation yields the coordinates of the intermediate point at t = 2/3.
In this way, we can use the Hermite interpolation formula to determine the intermediate points on the Hermite curve at t = 1/3 and t = 2/3 based on the given control points and tangent vectors.
Learn more about tangent here:
https://brainly.com/question/10053881
#SPJ11
if 2x – 1 is a factor of 16x4
24x3 + 2x + f, find f.
Answers
Answer:
f = -5
Step-by-step explanation:
If 2x – 1 is a factor of 16x4 + 24x3 + 2x + f, find f.
If 2x - 1 = 16x⁴ + 24x³ + 2x + f, find f.
2x - 1 = 0
2x = 1
x = 1/2
Hence
f(1/2) = 16(1/2)⁴ + 24(1/2)³ + 2(1/2) + f
= 16(1/16) + 24(1/8) + 1 + f
= 1 + 3 + 1 + f
= 5+ f
f = -5
How to form a polynomial with given zeros and degree?
Answers
To form a polynomial with given zeros and degree, we need to use the fact that if a polynomial has a zero of x = a, then it can be factored as (x - a) times some other polynomial.
This means that if we know the zeros of a polynomial, we can write it in factored form, and then multiply out the factors to get the polynomial in standard form.
The degree of the polynomial tells us how many factors are necessary. For example, if the degree is 3, we know that the polynomial can be factored into three linear factors, one for each zero.
To illustrate this process, let's say we want to form a polynomial of degree 4 with zeros of x = 2, x = -1, and x = 3. We would start by writing the polynomial in factored form as:
f(x) = (x - 2)(x + 1)(x - 3)(ax + b)
Since the degree is 4, we need to include one more factor. We can use the coefficients a and b to determine this factor. To do so, we can either use the value of the leading coefficient (which is a in this case) or a point on the polynomial (i.e., a value of x and f(x)).
Once we have determined the value of a, we can solve for b by setting a point on the polynomial equal to a known value.
Finally, we can multiply out the factors to get the polynomial in standard form:
f(x) = (x - 2)(x + 1)(x - 3)(2x - 4)
f(x) = 2x^4 - 8x^3 - 13x^2 + 22x - 12
In conclusion, to form a polynomial with given zeros and degree, we need to use the fact that a polynomial can be factored as (x - a) times some other polynomial if it has a zero of x = a.
We can write the polynomial in factored form, determine the missing factor(s) using the degree and coefficients, and then multiply out the factors to get the polynomial in standard form.
To learn more about polynomial click on,
https://brainly.com/question/14742650
#SPJ4
Which graph represents a function?

Answers
Remember that a function can only take on one output for each input.
You could do the Vertical Line Test on each of the given graphs to see if they represent a function. If a vertical line intersects the graph in all places at exactly one point, then the relation is a function.
Attached is the edited screenshot of your given set of graphs (sorry if it’s a bit sloppy, I’m using my phone to post this answer).
I drew vertical lines (in blue), and the small red marks in each line indicate the areas where each vertical line crosses the graph.
As the graphs show, graph M is the only graph that has 1 point in each vertical line. This implies that each input only has 1 corresponding output.
Therefore, graph M is a function.

Pleaseee helpp answer correctly !!!!!!!!!!!!!!! Will mark Brianliest !!!!!!!!!!!!!!!!!!!!

Answers
Answer:
4
Step-by-step explanation:
In a parallelogram AO and OC are equal. Therefore you should set up the equation 3x-4=8. When you add 4 to both sides you get 3x=12. When you divide both sides by 3 you get x=4
Solve for x.
JKL
2x-4
8
16
7
56

Answers
you have to use intercept theorem, also known as Thales's theorem to slove this problem

Can somebody plz help answer both word problem questions correctly thanks :DD
WILL MARK BRAINLIEST WHOEVER ANSWERS FIRST!!!:DDD
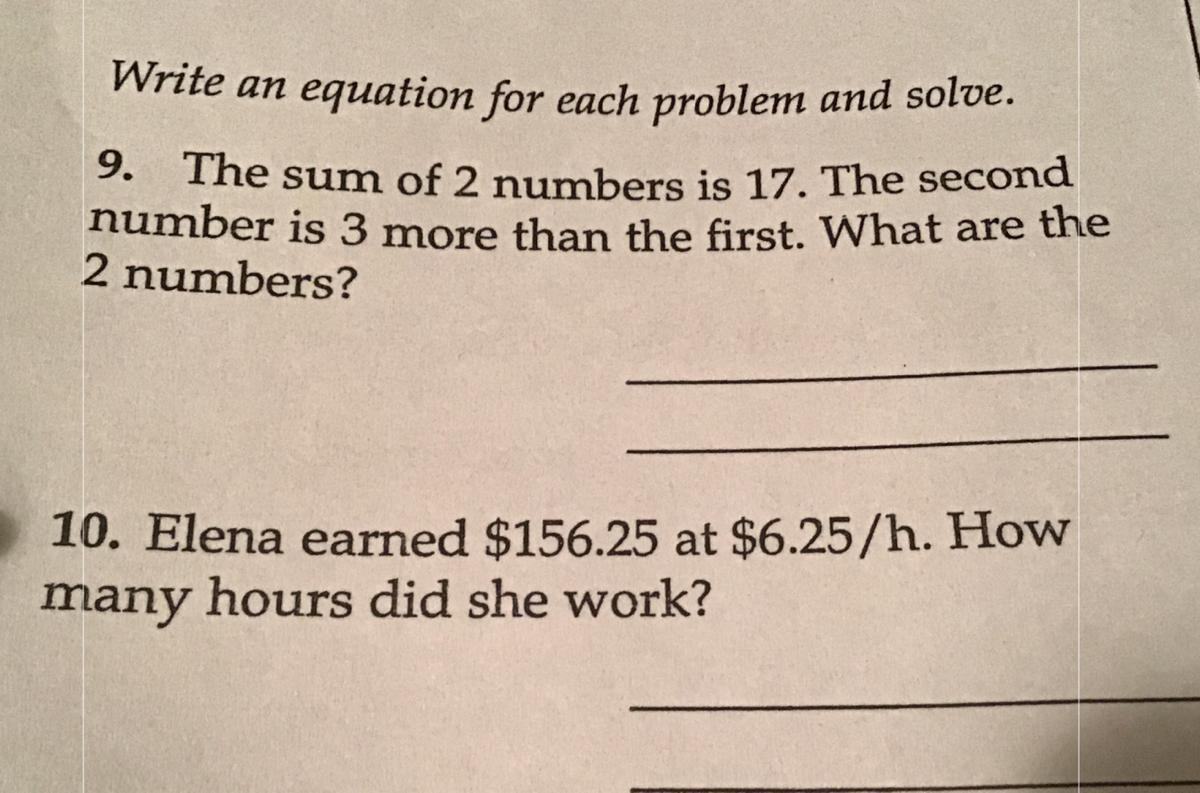
Answers
9. a+b=17
b=3+a
17=a+3+a
14=2a
7=a
b=3+7
b=10
10. 156.25/6.25= 25 hrs
Answer:
9. x = 7, y = 10
Step-by-step explanation:
9. I first set up an equation x+y=17
then I set up a second equation y = x+3
I substitute y for x+3 and get x+x+3=17 or 2x+3=17
then I just evaluate the equation x=7
I then use my first equation x+y = 17 and substitute the value 7+y= 17 and get y = 10
10. Just divide 156.25 with 6.25 to get the number of hours she had to work to get 156.25 dollars. The answer would be 156.25/ 6.25 = 25
can you help? \(5\sqrt{-27}\)
Answers
Answer:
\(15\sqrt{3}i\)
Step-by-step explanation:
Negative square roots are complex numbers.
HELP!!!! This is an escape room match the letters with the definition of the symbol

Answers
The required answers are 1) < 2) ≤ 3) ≤ 4) ≥ 5) ≤ 6) ≤.
What are Symbols?A mark, sign, or word that denotes, denotes, or is taken to denote a concept, an object, or a relationship is known as a symbol. By connecting seemingly unrelated ideas and events, symbols help people see beyond the known and the visible.
According to question:We have given some some symbols and some vocabulary. We need to match the correct vocab to correct symbol.
then,
1) Under is denoted by B. <
2) No more than denotes something that is less than or equivalent to. It is indicated by the symbol ≤ in disparity.
3 ) When a≤b are written together, it indicates that an is less than or equal to b.
4) At least denotes an amount larger than or equivalent to. It is indicated by the symbol ≥ in disparity. As a result, is the inequality sign for at least.
5) Minimum is a mathematical symbol for "less than or equal to," (≤)and it is used in many/some mathematical fields.
6) The word no more than means less than or equal to. In inequality, it denotes by the symbol ≤ .
To know more about Inequality visit:
brainly.com/question/30238995
#SPJ1
Use the order pairs to write a function rule. Give the tule in slope-intercept form.
{(-12,1.5),(-1,-1.25),(5,-2.75),(8,-3.5)}
Answers
to get the equation of any straight line, we simply need two points off of it, so hmmm let's use say (-1 , -1.25) and (8 , -3.5)
\((\stackrel{x_1}{-1}~,~\stackrel{y_1}{-1.25})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{-3.5}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-3.5}-\stackrel{y1}{(-1.25)}}}{\underset{run} {\underset{x_2}{8}-\underset{x_1}{(-1)}}}\implies \cfrac{-3.5+1.25}{8+1}\implies \cfrac{-2.25}{9}\implies -\cfrac{~~ \frac{225}{100}~~}{\frac{9}{1}} \\\\\\ -\cfrac{225}{100}\cdot \cfrac{1}{9}\implies -\cfrac{9}{4}\cdot \cfrac{1}{9}\implies -\cfrac{1}{4}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-1.25)}=\stackrel{m}{-\cfrac{1}{4}}(x-\stackrel{x_1}{(-1)}) \\\\\\ y+1.25=-\cfrac{1}{4}(x+1)\implies y+\cfrac{5}{4}=-\cfrac{1}{4}x-\cfrac{1}{4} \\\\\\ y=-\cfrac{1}{4}x-\cfrac{1}{4}-\cfrac{5}{4}\implies y=-\cfrac{1}{4}x-\cfrac{6}{4}\implies y=-\cfrac{1}{4}x-\cfrac{3}{2}\)
help I've got 5min to figure it out 20 points for 1st actual answer and brainlyist

Answers
Hoped this help
Find the conjugate of -6 - i.
Answers
The conjugate of -6-i is -6+i.
Complex numbers are those that are stated as "a+ib," where "a" and "b" are real numbers and "i" is an imaginary number known as "iota".A complex number is a combination of real and imaginary numbers.A complex number is a straightforward representation of the addition of two integers, namely a real number and an imaginary number. One portion is entirely real, while the other is entirely imaginary.The complex conjugate of a complex number is the number that has an equal real portion and an imaginary part that is equal in magnitude but opposite in sign.The given number (-6-i) is a complex number.The conjugate will be the number with the same real part but the negative of the imaginary part.Hence, the conjugate of the given is -6+i.To learn more about complex numbers, visit :
https://brainly.com/question/20566728
#SPJ1
How many 3/2 cup servings are in 9/2 cups of flours?

Answers
Answer:
3
Step-by-step explanation:
9 divided by 3 is 3
So, you can multiply 3/2 by 3 to get 9/2
Hope this helps! :)
Brianna is planting a sapling. The garden center recommended she stabilize the sapling with guy wires for the first few
months after planting. If Brianna places the guy wires 6 feet up the trunk of the sapling and 5 feet from the base, how
much total wire, to the nearest tenth of a foot, will she need for the two guy wires?
Answers
Answer:
your answer would be 7.8 feet
What are 3 ratios of 5:8
Answers
Answer:
5 to 8, 5/8 as a fraction, 5:8
Step-by-step explanation:
ratios can be written in word form, fractions, and like 5:8.
Answer:
5:8
5/8
5 to 8
Step-by-step explanation:
These are the three ways to correctly write a ratio. It's important to keep it in order - instead of 8/5 or 8:5 - do 5:8 or 5/8
For example:
The ratio of dogs to cats is 5:8
-kiniwih426
2) Imagine that you had discovered a relationship that would generate a scatterplot very similar to the relationship Y₁ = X, and that you would try to fit a linear regression through your data points. What do you expect the slope coefficient to be? What do you think the value of your regression R2 is in this situation? What are the implications from your answers in terms of fitting a linear regression through a non-linear relationship?
Answers
If the relationship discovered is very similar to Y₁ = X and a linear regression is fit through the data points, we would expect the slope coefficient to be approximately 1.
The value of the regression R2 in this situation would likely be high, indicating a good fit.
Expectation for the slope coefficient:
If the relationship discovered is very similar to Y₁ = X, we would expect the slope coefficient of the linear regression to be close to 1. This is because the equation Y = X represents a direct proportional relationship between the dependent variable (Y) and the independent variable (X), where a unit increase in X corresponds to a unit increase in Y.
Expected value of the regression R2:
In this situation, the regression R2 value would likely be high. R2 measures the proportion of the total variation in the dependent variable (Y) that is explained by the independent variable (X). Since the discovered relationship is very similar to Y₁ = X, a linear regression through the data points would likely result in a good fit, capturing a large portion of the variation in Y.
Implications of fitting a linear regression to a non-linear relationship:
Fitting a linear regression to a non-linear relationship can lead to biased estimates and inaccurate predictions. While the R2 value might indicate a good fit, it’s important to remember that the underlying relationship is non-linear. Linear regression assumes a linear relationship between the variables, and if the true relationship is non-linear, the estimates of the slope coefficient and other parameters may not accurately represent the relationship.
To properly capture the non-linear relationship, alternative regression techniques such as polynomial regression, exponential regression, or non-linear regression models should be considered.
Learn more about linear regression here : brainly.com/question/13328200
#SPJ11
Consider the function where xy U = for (x, y) = (0,0), x² + y² and v= = 0 for all x and y. X 2.1 Show that all partial derivatives of u and v exist at (x, y) = (0, 0), and thus satisfy the Cauchy- Riemann equations. (5) 2.2 Show that is not continuous at (0,0), and hence f is not differentiable at (0, 0). U (5) 2.3 Investigate whether f is analytic or not. (5) 2.4 Investigate whether f has a harmonic complex conjugate or not. (5) 2.5 Show that the function f (x, y) = x² - y² —y is harmonic and determine its harmonic conjugate. - f = u + iv,
Answers
2.1 To show that all partial derivatives of u and v exist at (x, y) = (0, 0) and satisfy the Cauchy-Riemann equations, we need to calculate the partial derivatives of u and v and check their existence and the Cauchy-Riemann conditions.
The function is given as u(x, y) = xy and v(x, y) = x² + y².
Partial derivatives of u:
∂u/∂x = y
∂u/∂y = x
Partial derivatives of v:
∂v/∂x = 2x
∂v/∂y = 2y
All partial derivatives exist at (x, y) = (0, 0) since they are simple functions and do not have any singularities.
Now, let's check if the Cauchy-Riemann equations are satisfied:
∂u/∂x = ∂v/∂y
y = 2y
This equation holds true for all values of y, including y = 0.
∂u/∂y = -∂v/∂x
x = -2x
This equation also holds true for all values of x, including x = 0.
Therefore, all partial derivatives of u and v exist at (x, y) = (0, 0), and they satisfy the Cauchy-Riemann equations.
2.2 To show that f is not continuous at (0, 0) and hence not differentiable at (0, 0), we can examine the behavior of f as (x, y) approaches (0, 0).
The function f(x, y) = u(x, y) + iv(x, y) = xy + i(x² + y²)
As (x, y) approaches (0, 0), both u(x, y) = xy and v(x, y) = x² + y² approach 0. However, f(x, y) = xy + i(x² + y²) approaches 0 + i(0) = i(0) = 0i = 0, which is a different value.
Therefore, f is not continuous at (0, 0), and hence it is not differentiable at (0, 0).
2.3 To investigate whether f is analytic or not, we need to check if it is differentiable in a neighborhood around every point.
Since we have already shown that f is not differentiable at (0, 0), it implies that f is not analytic because differentiability is a necessary condition for analyticity.
2.4 To investigate whether f has a harmonic complex conjugate or not, we need to check if u and v satisfy the Laplace's equation (∇²u = 0 and ∇²v = 0) and if they satisfy the Cauchy-Riemann equations.
The Laplace's equation is not satisfied by u(x, y) = xy because ∇²u = ∂²u/∂x² + ∂²u/∂y² = 0 + 0 ≠ 0.
Therefore, f does not have a harmonic complex conjugate.
2.5 To show that the function f(x, y) = x² - y² - iy is harmonic, we need to demonstrate that it satisfies the Laplace's equation (∇²u = 0 and ∇²v = 0).
For u(x, y) = x² - y², we have ∇²u = ∂²u/∂x² + ∂²u/∂y² = 2 - 2 = 0.
For v(x, y) = -y, we have ∇²v = ∂²v/∂x² + ∂²v/∂y² = 0 + 0 = 0.
Both u and v satisfy the Laplace's equation, indicating that f(x, y) = x² - y² - iy is a harmonic function.
To determine the harmonic conjugate of f, we can integrate the partial derivative of v with respect to x and y, and obtain the imaginary part of the function:
h(x, y) = ∫ (∂v/∂y) dy = ∫ 0 dy = C(y)
Where C(y) is an arbitrary function of y.
The harmonic conjugate of f is given by:
g(x, y) = u(x, y) + ih(x, y) = x² - y² + iC(y)
Therefore, the harmonic conjugate of f(x, y) = x² - y² - iy is g(x, y) = x² - y² + iC(y), where C(y) is an arbitrary function of y.
Learn more about Cauchy-Riemann here -: brainly.com/question/30385079
#SPJ11
To show that all partial derivatives of u and v exist at (x, y) = (0, 0) and satisfy the Cauchy-Riemann equations, we need to calculate the partial derivatives of u and v and check their existence and the Cauchy-Riemann conditions.
The function is given as u(x, y) = xy and v(x, y) = x² + y².
Partial derivatives of u:
∂u/∂x = y
∂u/∂y = x
Partial derivatives of v:
∂v/∂x = 2x
∂v/∂y = 2y
All partial derivatives exist at (x, y) = (0, 0) since they are simple functions and do not have any singularities.
Now, let's check if the Cauchy-Riemann equations are satisfied:
∂u/∂x = ∂v/∂y
y = 2y
This equation holds true for all values of y, including y = 0.
∂u/∂y = -∂v/∂x
x = -2x
This equation also holds true for all values of x, including x = 0.
Therefore, all partial derivatives of u and v exist at (x, y) = (0, 0), and they satisfy the Cauchy-Riemann equations.
2.2 To show that f is not continuous at (0, 0) and hence not differentiable at (0, 0), we can examine the behavior of f as (x, y) approaches (0, 0).
The function f(x, y) = u(x, y) + iv(x, y) = xy + i(x² + y²)
As (x, y) approaches (0, 0), both u(x, y) = xy and v(x, y) = x² + y² approach 0. However, f(x, y) = xy + i(x² + y²) approaches 0 + i(0) = i(0) = 0i = 0, which is a different value.
Therefore, f is not continuous at (0, 0), and hence it is not differentiable at (0, 0).
2.3 To investigate whether f is analytic or not, we need to check if it is differentiable in a neighborhood around every point.
Since we have already shown that f is not differentiable at (0, 0), it implies that f is not analytic because differentiability is a necessary condition for analyticity.
2.4 To investigate whether f has a harmonic complex conjugate or not, we need to check if u and v satisfy the Laplace's equation (∇²u = 0 and ∇²v = 0) and if they satisfy the Cauchy-Riemann equations.
The Laplace's equation is not satisfied by u(x, y) = xy because ∇²u = ∂²u/∂x² + ∂²u/∂y² = 0 + 0 ≠ 0.
Therefore, f does not have a harmonic complex conjugate.
2.5 To show that the function f(x, y) = x² - y² - iy is harmonic, we need to demonstrate that it satisfies the Laplace's equation (∇²u = 0 and ∇²v = 0).
For u(x, y) = x² - y², we have ∇²u = ∂²u/∂x² + ∂²u/∂y² = 2 - 2 = 0.
For v(x, y) = -y, we have ∇²v = ∂²v/∂x² + ∂²v/∂y² = 0 + 0 = 0.
Both u and v satisfy the Laplace's equation, indicating that f(x, y) = x² - y² - iy is a harmonic function.
To determine the harmonic conjugate of f, we can integrate the partial derivative of v with respect to x and y, and obtain the imaginary part of the function:
h(x, y) = ∫ (∂v/∂y) dy = ∫ 0 dy = C(y)
Where C(y) is an arbitrary function of y.
The harmonic conjugate of f is given by:
g(x, y) = u(x, y) + ih(x, y) = x² - y² + iC(y)
Therefore, the harmonic conjugate of f(x, y) = x² - y² - iy is g(x, y) = x² - y² + iC(y), where C(y) is an arbitrary function of y.
Learn more about Cauchy-Riemann here -: brainly.com/question/30385079
#SPJ11
After receiving a 45% discount, Mark bought a new camera for $245.99. What was the cost of the camera before the discount
Answers
Answer: $546.60 (*this was the actual number but I rounded it $546.644444444)
Step-by-step explanation:
Divide: $245.99/0.45 = 546.644444444
You can double check your answer by multiplying 546.644444444 by 0.45 and you will get $245.99
If you multiply by $546.60 you will get $245.97 since you rounded
PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!!PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!! PLSSS HELPPPP I WILLL GIVE YOU BRAINLIEST!!!!!!

Answers
the y intercept is -2
and the slope is 3/4
slope= change in y/change in x
I really need help..im confused

Answers
The coefficient of determination, also known as R-squared, represents the proportion of the dependent variable's variance that can be explained by the independent variable(s) in a regression model. A higher R-squared indicates a better fit of the model to the data and suggests that a greater proportion of the variation in the dependent variable (lobster length in this case) can be attributed to the independent variable (age).
In this scenario, the linear model has a coefficient of determination of 0.8724503, indicating that approximately 87% of the variation in lobster length can be explained by age. This suggests a strong relationship between age and length in a linear fashion.
Conversely, the exponential model has a lower coefficient of determination of 0.6730372, indicating that only about 67% of the variation in lobster length is associated with age. While this is still a moderate level of association, the linear model provides a better fit to the data and explains a higher proportion of the variation in length.
Therefore, based on the coefficient of determination, the linear model would be the better choice for projecting the length of a lobster.
Given P(x)=x^3 +2x^2 +4x+8. Write P in factored form (as a product of linear factors). Be sure to write the full equation, including P(x)=.
Answers
The factored form of the polynomial P(x) = x³ + 2x² + 4x + 8 is P(x) = (x + 1)(x² + x + 7). The quadratic factor x^2 + x + 7 cannot be further factored into linear factors with real coefficients.
To factor the polynomial P(x) = x³ + 2x² + 4x + 8, we can look for potential roots by applying synthetic division or by using synthetic substitution. In this case, we can start by trying small integer values as possible roots, such as ±1, ±2, ±4, and ±8, using the Rational Root Theorem.
By synthetic substitution, we find that -1 is a root of the polynomial. Dividing P(x) by (x + 1) using long division or synthetic division, we get:
P(x) = (x + 1)(x² + x + 7)
Now, we need to factor the quadratic expression x² + x + 7. However, upon factoring this quadratic expression, we find that it cannot be factored further into linear factors with real coefficients. Therefore, the factored form of P(x) is:
P(x) = (x + 1)(x² + x + 7)
Please note that the quadratic factor x² + x + 7 does not have any real roots. Therefore, the complete factored form of P(x) is as given above.
To know more about polynomial refer here:
https://brainly.com/question/11536910#
#SPJ11
Can someone pls help?

Answers
Answer: 2
Step-by-step explanation:
Because if u divide 12÷6=2 2×6=12
Answer: \(x=6\sqrt{3}\)
Step-by-step explanation:
\(x=\sqrt{12^{2}-6^{2} } =\sqrt{144-36} =\sqrt{108} =6\sqrt{3}\)
Line segment PQ is the result of reflecting line segment AB across the x-axis.P has coordinates of (2,-2) and Q has coordinates (8,-2). What’s is the length of line segment AB.
Answers
The length of the line segment AB such that PQ is the reflection of AB will be 6 units.
What is a line segment?A line section that can connect two places is referred to as a segment.
A line segment is just part of a big line that is straight and going unlimited in both directions.
If we reflect any curve about the x-axis then only the y coordinate changes its sign (x,y) → (x,-y).
Given PQ is a reflection of AB and P(2,-2) and Q (8,-2)
Therefore, A(2,2) and B(8,2).
The length of AB will be,
AB = √(8 - 2)² + (2-2)² = 6
Hence "The length of the line segment AB such that PQ is the reflection of AB will be 6 units".
For more about line segments,
https://brainly.com/question/25727583
#SPJ1