Solve the proportion: 1/4 = x/20
Answers
Answer:
5x?
Step-by-step explanation:
Answer:
= 5
Step-by-step explanation:
Multiply all terms by the same value to eliminate fraction denominators
1/4 = x/20
20 ⋅ 1/4 = 20 ⋅ /20
Simplify
= 5
Related Questions
an equation in slope-intercept form that passes through the points ( 14, -15) , ( 7, -15 ).
Answers

Evaluate 6 + (r + 5)2 if r=13 ; S =2
Answers
Answer:
42
Step-by-step explanation:
6 + 2r + 10
Input r=13 into the equation
6 + 2(13) + 10
6 + 26 + 10
32 + 10
42
Hope this helps!
Have a nice day!
If you find my answer helpful
Pls consider marking my answer as Brainliest! It would mean a lot!
Answer:
42
Step-by-step explanation:
6+(r+5)2; r=13, S=2
Lets plug in what we know
6+(13+5)2 (Solve what is in the parentheses)
6+(18)2 (The 2 behind the parentheses is the same as a 2 in front of the parentheses. You will still multiply by 2)
6+36
42
HALP PLEASEEEEEJHEHEHEHE

Answers
Answer:
Hello! answer B
What I did was concert them to percents so
1/8 is 12.5%
1/4 is 25%
1/2 is 50% so this clearly goes from least to greatest. Hope that helps!
how do you find the length of the hypotenuse when you have only the length of the altitude of the hypotensuse and a length of a leg?
Answers
Answer:
By using The Pythagorean Theorem:
\(/Hypotenuse/^{2} = /Length of altitude/^{2} + /Length of leg/^{2} \\)
/Hypotenuse/ = \(\sqrt\ /Length of altitude/^{2} + /Length of leg/^{2} \}\)
Step-by-step explanation:
The Pythagorean theorem states that: Given a Right-angled triangle, the square of the hypotenuse equals the sum of squares of the other two sides ( Here, being the length of the altitude and length of leg). That is,
\(/Hypotenuse/^{2} = /Length of altitude/^{2} + /Length of leg/^{2} \\) and hence,
/Hypotenuse/ = \(\sqrt\ /Length of altitude/^{2} + /Length of leg/^{2} \}\)
For example, If the length of the altitude is 4m and the length of leg is 3m. Using The Pythagorean theorem, the length of the hypotenuse will be
\(/Hypotenuse/^{2} = /Length of altitude/^{2} + /Length of leg/^{2} \\\/Hypotenuse/ = \sqrt{/Length of altitude/^{2} + /Length of leg/^{2}} \\/Hypotenuse/ = \sqrt{4^{2} + 3^{2} }\)
\(/Hypotenuse/ = \sqrt{16+9} \\/Hypotenuse/ = \sqrt{25} \\/Hypotenuse/ = 5m\)
The length of the hypotenuse for the given example will be 5m.
This is how to find the length of an hypotenuse.
solve this please and tell me how you did it
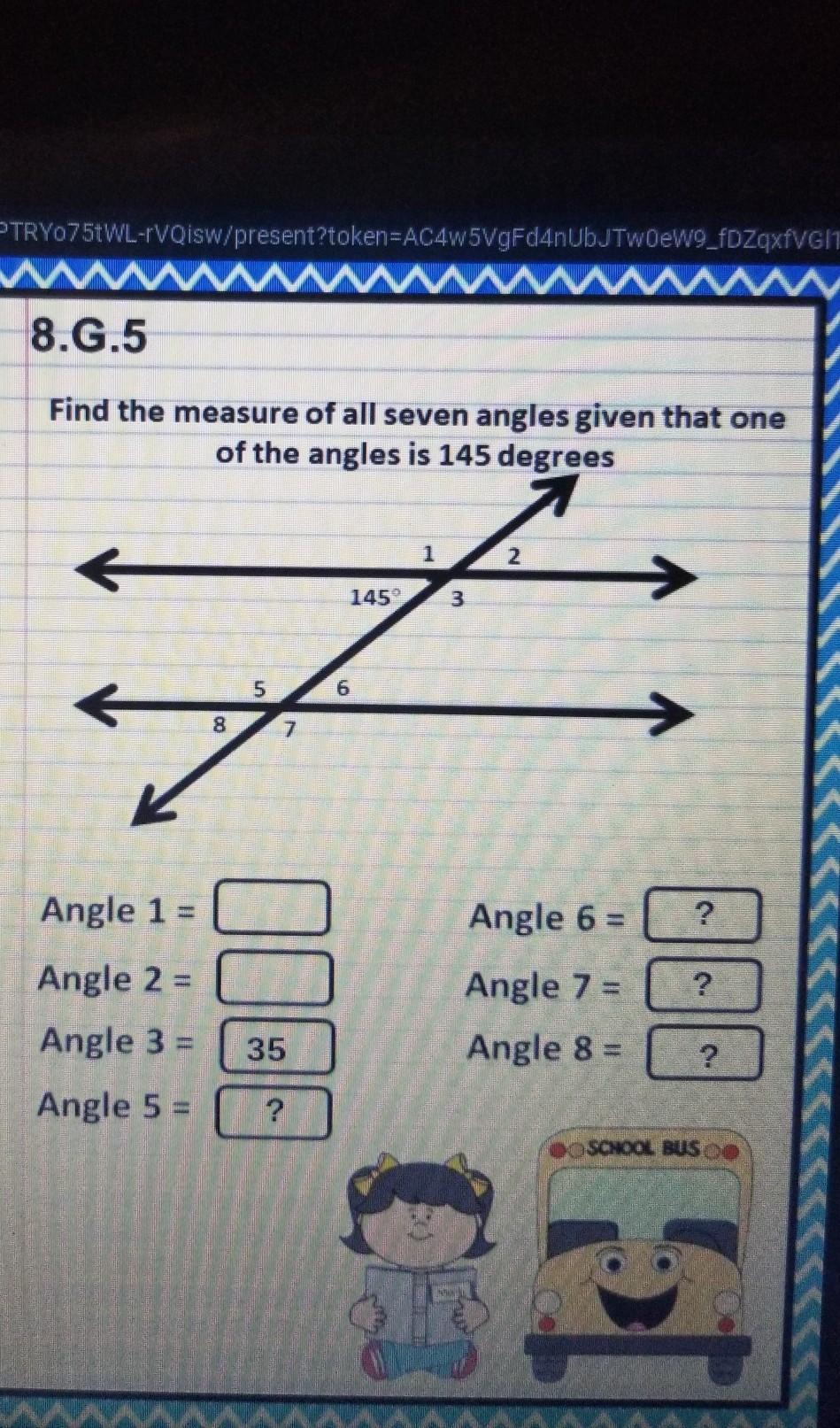
Answers
The angle ∠2 is a vertically opposite angle to the angle 145°, so they are congruent:
∠2 = 145°
The angles 1 and 3 are supplementary angles to the angle 145°, so they are equal to:
180° - 145° = 35°
∠1 = 35°
∠3 = 35°
The angle 8 is a corresponding angle to the angle 145°, so they are congruent:
∠8 = 145°
The angle ∠6 is a vertically opposite angle to the angle ∠8 so they are congruent:
∠6 = 145°
The angles 5 and 7 are supplementary angles to the angle ∠8, so they are equal to:
180° - 145° = 35°
∠5 = 35°
∠7 = 35°
What's the value of x?

Answers
Answer:
x= 31
Step-by-step explanation:
the yearly profits of a company is 25,000, the profits have been decreasing by 6% per year. write an exponential decay function to represent this
Answers
The yearly profits of a company is 25,000, the profits have been decreasing by 6% per year. write an exponential decay function to represent this?
Yearly profit = 25000 x e^ -0.06x
a binding less than or equal to (≤) constraint in a maximization problem meansa. the variable is up against an upper limit. b. the minimum requirement for the constraint has just been met. c. another constraint is limiting the solution. d. the shadow price for the constraint will be positive.
Answers
The variable is up against an upper limit. in a maximization problem, a binding less than or equal to (≤)
constraint indicates that the variable associated with the constraint has reached or is at its upper limit. It implies that the variable cannot increase further without violating the constraint.
This constraint acts as a restriction that limits the potential values the variable can take in the optimization problem.
When a constraint is binding, it means that the optimal solution to the problem is achieved when the constraint is satisfied with equality. In the context of a maximization problem,
if a variable is up against an upper limit and the constraint is binding, it suggests that the variable is already maximizing its value within the given constraint.
In contrast, if the constraint is not binding, it means that the variable has not reached its upper limit and has the potential to increase further while still satisfying the constraint. In such cases, the variable can be increased to improve the objective function value and optimize the problem further.
It's important to note that the shadow price, also known as the dual value or marginal value, represents the rate of change of the objective function with respect to a constraint. It indicates the sensitivity of the objective function to changes in the constraint.
The sign of the shadow price is not determined by the direction of the constraint (≤ or ≥), but rather by the problem formulation and the specific constraints and variables involved.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
What is the number 2.0847 to 2 decimal places?
Answers
Answer:
2.08
Step-by-step explanation:
A building is constructed using bricks that can be modeled as right rectangular prisms with a dimension of 7 1/4 by 3,3 1/4 in. If the bricks weigh 0.08 ounces per cubic inch and cost $0.07 per ounce, find the cost of 250 bricks. Round your answer to the nearest cent.
Answers
Can someone help me with these?
Answers
A spherical balloon is inflating with helium at a rate of 128x ft3 How fast is the balloon's radius increasing at the instant the radius is 4 t? min Write an equation relating the volume of a sphere, V, and the radius of the sphere, r (Type an exact answer, using π as needed.) Differentiate both sides of the equation with respect to t dV dt (Type an exact answer, using π as needed. Type an expression using r as the variable.) dr dt ▼1 at the instant the radius is 4 ft. The balloon's radius is increasing at a rate of Simplify your answer.) Enter your answer in each of the answer boxes.
Answers
The balloon's radius is increasing at a rate of 2x/π ft/min at the instant when the radius is 4 ft.
To solve this problem, we need to use the formula for the volume of a sphere, which is V = (4/3)πr^3.
We are given that the balloon is inflating with helium at a rate of 128x ft^3, which means that the rate of change of volume with respect to time is dV/dt = 128x.
We are asked to find how fast the balloon's radius is increasing at the instant when the radius is 4 ft and t = min. To do this, we need to differentiate the formula for the volume of a sphere with respect to time:
dV/dt = 4πr^2 (dr/dt)
We can rearrange this equation to solve for dr/dt:
dr/dt = (1/(4πr^2)) dV/dt
At the instant when the radius is 4 ft, we have r = 4, so we can plug in these values:
dr/dt = (1/(4π(4^2))) (128x) = (1/64π) (128x) = 2x/π ft/min
Finally, we can write the equation relating the volume of a sphere and the radius of the sphere as:
V = (4/3)πr^3
To differentiate this equation with respect to time, we get:
dV/dt = 4πr^2 (dr/dt)
And substituting the given value for dV/dt, we get:
128x = 4πr^2 (dr/dt)
Know more about volume of a sphere here:
https://brainly.com/question/9994313
#SPJ11
2x + y = -8
3x - 5y = -25
It’s substitution
Answers
Answer:
x = -5 , y = 2
Step-by-step explanation:
Solve the following system:
{y + 2 x = -8
-5 y + 3 x = -25
Hint: | Choose an equation and a variable to solve for.
In the first equation, look to solve for y:
{y + 2 x = -8
-5 y + 3 x = -25
Hint: | Solve for y.
Subtract 2 x from both sides:
{y = -2 x - 8
-5 y + 3 x = -25
Hint: | Perform a substitution.
Substitute y = -2 x - 8 into the second equation:
{y = -2 x - 8
3 x - 5 (-2 x - 8) = -25
Hint: | Expand the left hand side of the equation 3 x - 5 (-2 x - 8) = -25.
3 x - 5 (-2 x - 8) = (10 x + 40) + 3 x = 13 x + 40:
{y = -2 x - 8
13 x + 40 = -25
Hint: | Choose an equation and a variable to solve for.
In the second equation, look to solve for x:
{y = -2 x - 8
13 x + 40 = -25
Hint: | Isolate terms with x to the left hand side.
Subtract 40 from both sides:
{y = -2 x - 8
13 x = -65
Hint: | Solve for x.
Divide both sides by 13:
{y = -2 x - 8
x = -5
Hint: | Perform a back substitution.
Substitute x = -5 into the first equation:
{y = 2
x = -5
Hint: | Sort results.
Collect results in alphabetical order:
Answer: {x = -5 , y = 2
Find the value of x.

Answers
First find the sum of the interior angles.
Use (n-2)180=sum Remember n is the number of sides
(5-2)180= 3(180)= 540
Then all inside angles equal 540
Now solve for x
70+125+x-15+x-45+x+20=540
3x+165=540
3x=375
X=125
Which number should be added to
both sides of this quadratic equation
to complete the square?
(-3/2)² + 1 = x² − 3x + (-3/2)²

Answers
Answer:
9/4
Step-by-step explanation:
You want to know the value required to complete the square in the equation 1 = x² -3x.
PictureYour picture shows the required value: (-3/2)² = 9/4.
<95141404393>
plz help! what is the end of behavior of f(x)?

Answers
Answer:
B
Step-by-step explanation:
The end behavior of a function is how the graph behaves as it approaches negative and positive infinity.
Let's take a look at each end.
As x approaches negative infinity:
As x approaches the left towards negative infinity, we can see that the graph is shooting straight upwards.
Therefore, as \(x\rightarrow-\infty\), our function f(x) is increasing and increasing up towards positive infinity.
Therefore, the end behavior at the left will be:
\(\text{As } x\rightarrow-\infty, f(x)\rightarrow\infty\)
As x approaches (positive) infinity:
As x approaches the right towards positive infinity, we can see the that graph is also shooting straight upwards.
Therefore, the end behavior will be exactly the same. As x approaches positive infinity, f(x) also approaches positive infinity.
Therefore, the end behavior at the right will be:
\(\text{As } x\rightarrow \infty, f(x)\rightarrow \infty\)
Therefore, our answer is B.
work out how many verticies on a square based pyrimid are formed

Answers
Answer:
5 faces, 8 edges and 5 vertices, and could I please have Brain? I only need one more, I can't wait to help more people:DDD!
Step-by-step explanation:
5 faces, 8 edges and 5 vertices.
help please:) i’m trying to get all of this work completed but i just don’t understand it

Answers
\(\pi r^{2} =\\3,14*4^{2} \\3,14*16\\=50.24\)
Alright another here we go, Please help!

Answers
Answer:
4x=y
Step-by-step explanation:
4x=y is your answer because if x is 5, like in the table, then 4(5) would equal 20, which is the y-value. It also works for every number in the table.
Hope this helps.
One angle of an isosceles triangle measures 90°. Which other angles could be in that isosceles triangle? Choose all that apply. 45, 65, 30,15.
Answers
Answer:
45°
Step-by-step explanation:
(180-90)/2 = 90/2 = 45°
The answer is 45°.
Step-by-step explanation:
Hey there!
Since it is an isoceles triangle two angles must be equal.
Also, one angle is 90°. To find other angles, let's suppose one angle as "X", then next angle is also "X". {Since it is an isoceles triangle}.
Then;
x+x+90° = 180° { Sum of interior angles of a triangle is 180°}
or, 2x + 90° = 180°
or, 2x= 180° - 90°
or, 2x = 90°
or, X= 90°/2
or, X=45°.
Therefore, the other angles are 45° and 45°.
Hope it helps!
a six foot man standing 200 feet from a tower observes the angle of elevation to the top of the tower to be 67 degrees. how high is the tower?
Answers
So, the height of the tower is approximately 363.6 feet.
You can use trigonometry to solve this problem.
If we call the height of the tower "h" and the distance between the man and the base of the tower "d", then the angle of elevation is defined as the angle between the line of sight from the observer to the top of the tower and the horizontal line.
We can use the tangent function to relate the angle of elevation to the height and distance.
tan(67) = h/d
We know that the distance between the man and the tower is 200 feet. We can use this information to find the height of the tower.
h = d * tan(67)
h = 200 * tan(67)
The height of the tower is approximately 363.6 feet.
Please note that due to the approximation of the trigonometric functions, the answer may not be exactly as calculated.
To learn more about angle of elevation
Visit; brainly.com/question/16716174
#SPJ4
5. What is "Data Triangulation" in general? Give 2 real-world examples.
Answers
Data triangulation is a research method that involves using multiple data sources or methods to gather and analyze information, enhancing the validity and comprehensiveness of findings.
Data triangulation is a research method that involves using multiple sources or methods to gather and analyze data on a particular topic or research question. By combining different data sources, researchers aim to enhance the validity, reliability, and comprehensiveness of their findings.
Two real-world examples of data triangulation are:
Qualitative-Quantitative Triangulation in Market Research: In market research, qualitative methods like focus groups or interviews can be combined with quantitative methods like surveys or sales data analysis. By triangulating these data sources, researchers can gain a deeper understanding of consumer preferences, behaviors, and market trends, combining the richness of qualitative insights with the statistical power of quantitative data.Methodological Triangulation in Educational Research: In educational research, methodological triangulation can be employed by using multiple research methods to investigate a learning phenomenon. For example, a researcher may use classroom observations, interviews with teachers, and student performance data to gain a comprehensive understanding of a teaching strategy's effectiveness. By triangulating these data sources, the researcher can capture a more complete picture of the learning environment and draw robust conclusions.Learn more about Data Triangulation at
https://brainly.com/question/30027711
#SPJ4
The graph of quadratic function f has zeros of -8 and 4 and a maximum at (-2,18). What is the value of a in the function’s equation?
Answers
To find the equation of a parabola given the vertex and the zeroes, we can use the intercept form equation to help us:
\(y=a(x-r)(x-s)\)
r and s = intercepts/zeros of the graphSolving the QuestionWe're given:
Zeros: -8, 4Maximum: (-2, 18)\(y=a(x-r)(x-s)\)
⇒ Plug in the given information:
\(y=a(x-(-8))(x-4)\\18=a(-2-(-8))(-2-4)\\18=a(-2+8)(-2-4)\\18=a(6)(-6)\\18=a(-36)\\1=-2a\\\\a=-\dfrac{1}{2}\)
Answer\(a=-\dfrac{1}{2}\)
Find from first principles the derivative of cos x
Answers
Answer:
Please see the explanation.
Step-by-step explanation:
Let
\(f\left(x\right)=cosx\)
By the first principle
\(f\:'\left(x\right)=\lim _{h\to 0}\left(\frac{f\left(x+h\right)-f\left(x\right)}{h}\right)\)
\(=\lim _{h\to 0}\left(\frac{cos\:\left(x+h\right)-cos\:x}{h}\right)\)
\(=\lim _{h\to 0}\left[\frac{cos\:x\:cos\:h-sin\:x\:sin\:h\:-\:cos\:x}{h}\right]\)
\(=\lim _{h\to 0}\left[\frac{-cos\:x\left(1-cos\:h\right)-sin\:x\:sin\:h\:}{h}\right]\)
\(=\lim _{h\to 0}\left[\frac{-cos\:x\left(1-cos\:h\right)\:}{h}-\frac{sin\:x\:sin\:h}{h}\right]\)
\(=-cosx\:\left(\lim \:_{h\to \:0\:}\frac{1-cos\:h}{h}\right)-sin\:x\:\lim \:\:_{h\to \:\:0}\:\left(\frac{sin\:h}{h}\right)\)
\(=-cosx\:\left(0\right)-sinx\left(1\right)\)
\(=-sin\:x\)
Solve the triangle
NEED ASAP!!!

Answers
Answer:
Step-by-step explanation:
∠Q = tan⁻¹(2/6) = 18.4⁰
∠P = tan⁻¹(6/2) = 71.6⁰
(PQ)² = 6² + 2² = 40
PQ = √40 = 6.32
10(b+2)+3=73 distributive property
Answers
Answer:
b = 5
Step-by-step explanation:
10(b+2) + 3 = 73
10b + 20 + 3 = 73
10b = 50
∴ b = 5
find the area of the circle. Use 3.14 for pie. Do not round your answer.

Answers
Answer: A = 452.16 ft²
Step-by-step explanation:
This gives us the formula to solve for the area.
A = πr²
The radius (r) is the same as the diameter divided by 2.
24 ft / 2 = 12 ft
We will input these given values and solve.
A = πr²
A = (3.14)(12)²
A = 452.16 ft²
Answer:
452.16 ft²
Step-by-step explanation:
To find the radius, you divide the diameter (24) by 2, which equals 12. The area of a circle formula is πr². To find area, you do 12² * 3.14. That equals 144 * 3.14, which equals 452.16.
simplify. 3+9⋅7−8÷2
A= 29
B= 38
C= 62
D= 80
Answers
Steps to solve:
3 + 9 * 7 - 8 / 2
~Multiply
3 + 63 - 8 / 2
~Divide
3 + 63 - 4
~Add
66 - 4
~Subtract
62
Best of Luck!
What is the area of a triangle where the vertices are (-3,-3), (-3,2), and (1,2)
Answers
Given:
The vertices of the triangle are (-3,-3), (-3,2), and (1,2).
Required:
We need to find the area of the given triangle.
Explanation:
Mark the points on the graph and join them.
A(-3,2), B(-3,-3), and C(1,2).
The given triangle is a right-angled triangle.
The height of the given triangle is the length of AB.
The base length of the given triangle is the length of AC.
Consider the distance formula.
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)Use the distance formula to find the length of the line segments.
Consider the points A(-3,2) and B(-3,-3),
\(Substitute\text{ }x_1=-3,y_1=2,x_2=-3\text{ and }y_2=-3\text{ in the formula.}\)\(AB=\sqrt{(-3-(-3))^2+(-3-2)^2}\)\(AB=\sqrt{(0)^2+(-5)^2}\)\(AB=5units\)Consider the points A(-3,2) and C(1,2).
\(Substitute\text{ }x_1=-3,y_1=2,x_2=1\text{ and }y_2=2\text{ in the formula.}\)\(AC=\sqrt{(1-(-3))^2+(2-2)^2}\)\(AC=\sqrt{(4)^2+(0)^2}\)\(AC=4\)We get h=AB=5 and b=AC=4.
Consider the area of the triangle formula.
\(A=\frac{hb}{2}\)Substitute h=5 and b=4 in the formula.
\(A=\frac{5\times4}{2}\)\(A=10units^2\)Final answer:
\(A=10units^2\)
You cannot compare the value of rational and irrational numbers true or false
Answers
Answer:
true
Step-by-step explanation:
A rational number cannot be an irrational number.