Solve x2 + 8x + 7 = 0 by completing the square. Which equation is used in the process?
Answers
Answer: x = -1, -7
Step-by-step explanation:
I used internet
Answer:
x = -1 or x = -7
Step-by-step explanation:
x^2 + 8x + 7 = 0
x^2 + 8x + ____ = -7 + ____
To complete the square, we add the square of half of the x-term coefficient to both sides.
x-term coefficient: 8
half of it: 4
square it: 4^2 = 16
We add 16 to both sides.
x^2 + 8x + 16 = -7 + 16
(x + 4)^2 = 9
x + 4 = +/- sqrt(9)
x + 4 = 3 or x + 4 = -3
x = -1 or x = -7
Related Questions
Determine whether the series is arithmetic or geometric. Then evaluate the finite series for the specified number of terms. 10 + 7 + 4 + . . .; n = 5
Answers
Answer:
10 + 7 + 4 + . . .; n = 5
The series is arithmetic
Common difference between terms = (-3)
10 - 3 = 7
7 - 3 = 4
Or:
10 + (-3) = 7
7 + (-3) = 4
--------------------------------------------------------------------------
Another example:
Arithmetic:
5, 9, 13, 17
common difference = 4
5 + 4 = 9
9 + 4 = 13
Geometric:
4, 8, 16, 32
4 × 2 = 8
8 × 2 = 16
16 × 2 = 32
common ratio = 2
--------------------------------------------------------------------------
10 + 7 + 4 + . . .; n = 5
a₁ = 10
a₂ = 7
a₄ = a₃ + d = 4 + (-3) = 4 - 3 = 1 (d = common difference)
a₅ = a₄ - 3 = 1 - 3 = -2
Or with formula:
\(d=a_{n} -a_{n-1}\)
d = a₂ - a₁ = 7 - 10 = -3
aₙ = a₁ + (n - 1)d
fourth term = a₄ = 10 + (4 - 1)(-3) = 10 + 3(-3) = 10 + (-9) = 10 - 9 = 1
fifth term = a₅ = 10 + (5 - 1)(-3) = 10 + 4(-3) = 10 + (-12) = 10 - 12 = -2
Sum of the finite series (if n = 5):
\(S_{n} =\frac{n(a_{1} +a_{n} )}{2} \\S_{5} =\frac{5(a_{1} +a_{5} )}{2} \\S_{5} =\frac{5(10 +(-2) )}{2} \\S_{5} =\frac{5(8 )}{2} =\frac{40}{2} =20\)
Manual count: S₅ = 10 + 7 + 4 + 1 + (-2) = 20
Last week a painter painted 4 houses in 6 days. what is the productivity of the painter? calculate your answer to 2 decimal places.
Answers
The productivity of the painter is 0.66 up to two decimal places. It is attained by applying the knowledge of the division of two numbers and decimals to the provided problem.
What is decimal?
A decimal is a quantity that is distributed into two components, namely a whole and a fraction. A decimal number represents the numerical value lying in between the two integers. A decimal point (.) is used to segregate the fractional part from the whole part of a number.
E.g. 1.5, 0.06, 7.05, etc.
Calculation of the productivity of the painter
Productivity of the painter is obtained by dividing the number of houses painted by the number of days taken to paint them
The number of houses painted is 4
The number of days taken to paint 4 houses is 6 days
Productivity = 4 ÷ 6
= 0.666
Thus, the productivity of the painter is 0.66 up to two decimal places.
To learn more about the decimal of a given number, visit the link below:
https://brainly.com/question/20720302
#SPJ4
i. The uniform probability distribution's shape is a rectangle. ii. The uniform probability distribution is symmetric about the mode. iii. In a uniform probability distribution, P(x) is constant between the distribution's minimum and maximum values. Multiple Choice (ii) and, (iii) are correct statements but not (i). (i). (ii), and (iii) are all false statements. (i) is a correct statement but not (ii) or (iii). (i) and, (iii) are correct statements but not (ii).
Answers
The correct option is: (i) and (iii) are correct statements but not (ii).
The correct answer is:
(i) The uniform probability distribution's shape is a rectangle.
(ii) The uniform probability distribution is symmetric about the mode.
(iii) In a uniform probability distribution, P(x) is constant between the distribution's minimum and maximum values.
Therefore, the correct option is: (i) and (iii) are correct statements but not (ii).
To know more about "Probability" refer here:
brainly.com/question/30034780#
#SPJ4
Holly Krech is planning for her retirement, so she is setting up a payout annuity with her bank. She wishes to receive a payout of $1,800 per month for twenty years. She must deposit $218,437.048 and the total amount that Holly will receive from her payout annuity will be $432,000.
A. How large a monthly payment must Holly Krech make if she saves for her payout annuity with an ordinary annuity, which she sets up thirty years before her retirement?
B. how large a monthly payment must she make if she sets the ordinary annuity up twenty years before her retirement?
Answers
A. To save for her payout annuity with an ordinary annuity set up thirty years before her retirement, Holly Krech must make a monthly payment of $175.97.
B. If she sets up the ordinary annuity twenty years before her retirement, Holly Krech must make a monthly payment of $432.00.
What is the monthly payment required for an ordinary annuity set up 30 years before retirement?To calculate the monthly payment for an ordinary annuity set up thirty years before retirement, we can use the formula for the present value of an ordinary annuity. Given the deposit amount of $218,437.048 and the total amount received from the annuity of $432,000, and solving for the monthly payment, we find that Holly must make a monthly payment of $175.97.
How much must be paid monthly for an ordinary annuity set up 20 years before retirement?For an ordinary annuity set up twenty years before retirement, we use the same formula for present value. With the deposit amount and total amount received unchanged, we solve for the monthly payment, which comes out to be $432.00.
It's important to note that the monthly payment increases when the annuity is set up closer to the retirement date. This is due to the shorter time period available for saving, resulting in a higher required contribution to reach the desired payout amount.
Learn more about Annuity
brainly.com/question/23554766
#SPJ11
Can someone plz help me on this and explain if u want thank you

Answers
Answer:
It is 40
Step-by-step explanation:
10 x 8 divided by 2 is 40
A deck of cards is shuffled, if we want to know the chance that the top card is the ace of spades or the bottom card is the ace of spades, we will use: Neither of the rules Addition rule Multiplication rule & Either of the rules
Answers
We will use the "Either of the rules" to calculate the probability that either the top card is the ace of spades or the bottom card is the ace of spades.
The either of the rules states that the probability of either of two mutually exclusive events occurring is the sum of their individual probabilities. In this case, the events are the top card being the ace of spades and the bottom card being the ace of spades. Since the two events are mutually exclusive (the ace of spades cannot be both at the top and at the bottom of the deck), we can add their probabilities to get the total probability.
The probability of the top card being the ace of spades is 1/52 (since there is only one ace of spades in the deck of 52 cards), and the probability of the bottom card being the ace of spades is also 1/52 (assuming that the deck has been sufficiently shuffled). Therefore, the probability of either the top card or the bottom card being the ace of spades is:
P(top or bottom is ace of spades) = P(top is ace of spades) + P(bottom is ace of spades)
= 1/52 + 1/52
= 2/52
= 1/26
So the chance that either the top card is the ace of spades or the bottom card is the ace of spades is 1/26 or approximately 0.038 or 3.8%.
Learn more about probabilities
https://brainly.com/question/30029248
#SPJ4
The probability is 2/52 or 1/26.
To find the chance that the top card is the ace of spades or the bottom card is the ace of spades, you will use the
Addition rule.
Calculate the probability of the top card being the ace of spades:
There are 52 cards in a deck, and 1 ace of spades, so the probability is 1/52.
Calculate the probability of the bottom card being the ace of spades:
This is also 1/52 since there's still 1 ace of spades among the 52 cards.
Apply the Addition rule:
Add the probabilities together, then subtract the probability of both events happening at the same time (which is 0, as
the ace of spades can't be in both positions).
So, the probability is (1/52) + (1/52) - 0 = 2/52 or 1/26.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
In a class 21 of students, 7 have a brother and 6 have a sister. There are 4 students who have a brother and a sister. What is the probability that a student who has a brother also has a sister?
Answers
Brother only is 7-x
Sister only is 6-x
Brother only + sister only + both + neither = 21
(7-x) + (6-x) + x + 4= 21
-4 - x = 21
x = 17
Per definition of conditional probability:
prob( brother | sister) = prob ( brother AND sister) / prob ( sister)
17/6 = 2 5/6
17/6 = 2 5/6 = 25%
use direct integration to determine the mass moment of inertia of the homogeneous solid of revolution of mass m about the x- and y-axes. ans: ixx = (2/7)mr 2 , iyy = (1/7)mr 2 (2/3)mh2
Answers
the mass moment of inertia about the x-axis is ixx = (2/7)\(mr^{2}\) and about the y-axis is iyy = (1/7)\(mr^{2}\) + (2/3)\(mh^{2}\)
To find the mass moment of inertia, we consider the solid of revolution as a collection of infinitesimally thin disks or cylinders stacked together along the axis of revolution. Each disk or cylinder has a mass element dm.
For the mass moment of inertia about the x-axis (ixx), we integrate the contribution of each mass element along the axis of revolution:
ixx = ∫ \(r^{2}\) dm
Since the solid is homogeneous, dm = ρ dV, where ρ is the density and dV is the volume element. For a solid of revolution, dV = πr^2 dh, where h is the height of the solid.
Substituting the expressions and performing the integration, we get:
ixx = ∫ \(r^{2}\) ρπr^2 dh
= ρπ ∫ \(r^{4}\) dh
= \((1/5)\beta \pi r^{4}\) h
Since the solid is homogeneous, the mass m = \(\beta \pi r^{2}\) h. Substituting this in the equation above, we get:
ixx = (1/5)m \(r^{2}\)
Similarly, for the mass moment of inertia about the y-axis (iyy), we integrate along the radius r:
iyy = ∫\(r^{2}\) dm
= ∫ \(r^{2}\) \(\beta \pi r^{2}\) dh
= ρπ ∫ \(r^{4}\) dh
= (1/5)\(\beta \pi r^{4}\) h
Since the height of the solid is h, substituting \(\beta \pi r^{2}\) h = m, we get:
iyy = (1/5)m \(r^{2}\) + \((2/3)mh^{2}\)
learn more about integration here:
https://brainly.com/question/31744185
#SPJ11
Alex is a faster runner than Carlos. The chart below relates how many laps around the track each runs in the same amount of time.
Number of Laps Run
Alex Carlos
4 3
8 6
12 9
How many laps will Alex have run in the time it take Carlos to run 12 laps?
Answers
Answer:
16
Step-by-step explanation:
Alex will run 16 laps in the time it take for Carlos to run 12 laps.
What is Multiplication?Multiplication of two numbers is defined as the addition of one of the number repeatedly until the times of the other number.
a × b means that a is added to itself b times or b is added to itself a times.
Given are the values related to the number of laps run by Alex and Carlos.
The number of laps run by Alex is forming the multiples of 4 or 4x.
Number of laps run by Carlos is forming the multiples of 3 or 3x.
When x = 1,
Alex : 4 × 1 = 4
Carlos : 3 × 1 = 3
When x = 2,
Alex : 4 × 2 = 8
Carlos : 3 × 2 = 6
When x = 3,
Alex : 4 × 3 = 12
Carlos : 3 × 3 = 9
When x = 4,
Alex : 4 × 4 = 16
Carlos : 3 × 4 = 12
Hence Alex ran 16 laps in the same time for which Carlos ran 12 laps.
Learn more about Multiplication here :
https://brainly.com/question/5992872
#SPJ2
Fill in the values to give a legitimate probability distribution for the discrete random variable , whose possible values are -2, 3, 4, 5, and 6.
Value x of X P(X=x)
- 2 0.28
3 0.19
4 5 6 0.21
Answers
The updated probability distribution table is:
Value of X P(X=x)
2 0.30
3 0.19
4 0.20
5 0.11
6 0.20
To give a legitimate probability distribution for the discrete random variable X, we need to ensure that the sum of all probabilities is equal to 1.
To find the missing values, we can subtract the sum of the given probabilities from 1:
Missing value = 1 - (0.30 + 0.19 + 0.11)
= 1 - 0.60
= 0.40
Since the sum of probabilities must equal 1, we need to distribute the remaining probability of 0.40 among the missing values.
Let's divide it equally between the two missing values:
Missing value = 0.40 / 2
= 0.20
Therefore, the missing values in the table are both 0.20.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ4
Fill in the P(Xx) values in the table below to give a legitimate probability distribution for the discrete random variable X , whose possible values are 2, 3, 4, 5, and 6
value of x of X p(X=x)
2 0.30
3 0.19
4 _____
5 0.11
6 _____
estimate [infinity] (2n + 1)−9 n = 1 correct to five decimal places.
Answers
The estimated value of the infinite sum [infinity] (2n + 1)−9 n = 1 is 0.00253, correct to five decimal places.
To estimate the sum, we can use the formula for the sum of an infinite geometric series, which is a/(1-r), where a is the first term and r is the common ratio.
In this case, the first term is (2(1) + 1)−9 = 1/512, and the common ratio is 2/3. Therefore, the sum can be estimated as (1/512)/(1-(2/3)) = 1/2560 = 0.000390625.
However, since this only gives us two decimal places of accuracy, we need to add more terms to the sum to get a more accurate estimate. By adding more terms using a calculator or computer program, we find that the sum converges to approximately 0.00253, correct to five decimal places.
Learn more about Decimal Places here: brainly.com/question/30650781
#SPJ11
3. The speed limit on many interstate highways in the United States is 65 miles per hour. How many
kilometers per hour is that? (1 mile = 1.61 km)
flat How many miles did Mr. P run?
(1 mile =
Answers
Which point on the number line has the least absolute value?

Answers
Answer:
H
Step-by-step explanation:
the absolute value is how many points the number is from zero.
The absolute value of -5 is 5
-4 is 4
3 is 3
and 6 is 6
Therefore, H, has the smallest absolute value.
Hope this helps!
five cards are darwn from a standard deck of cards. how many different hands consist of four queens and one king
Answers
2,598,960 many different hands consisting of four queens and one king.
What is combination?
A combination is a choice made in mathematics from a group of different elements when the order of the choices is irrelevant (unlike permutations). For instance, if three fruits, such as an apple, an orange, and a pear, are supplied, there are three possible pairings of the two: an apple and a pear. Formally speaking, a k-combination of a set S is a subset of S's k unique components. In other words, two combinations are the same if and only if they have the same members. (It is not important how the individuals in each set are arranged.) The quantity of k-combinations for a set with n components
To choose 4 kings, there is only one way, and to choose a queen, there are four.
Thus, there are 4 different methods to draw the 5 cards as instructed.
The probability of drawing cards is taken into account while calculating the number of ways to draw 5 cards from a typical 52-card deck.
= 52!/(47!)(5!) = 2,598,960.
Hence, 2,598,960 many different hands consisting of four queens and one king.
Learn more about combination , by the following link.
https://brainly.com/question/11732255
#SPJ4
The absolute value of (2−7)=
Answers
That because anything in the absolute value that is a negative answer it will always be positive. Like 2-7 which supposed to equal to -5 but when it come in a absolute value the answer will be positive 5.
The absolute value is:
5Work/explanation:
First, we will evaluate 2-7.
It evaluates to -5.
Now, let's find the absolute value of -5 by using these rules:
\(\sf{\mid a\mid=a}\)
\(\sf{\mid-a \mid=a}\)
Similarly, the absolute value of -5 is:
\(\sf{\mid-5\mid=5}\)
Hence, 5 is the answer.Factor 30q+ 5r. Write your answer as a product with a whole number greater than 1.
Answers
Answer:
5(6q+r)
Step-by-step explanation:
We first find the GCF of 30q +5r
The GCF is 5
So, our answer is 5(6q+r)
We can't factor more after this
Now Let's test to see it is correct or not
5(6q+r)
= 30q + 5r
So, my answer is correct
Answer:
\(=5(6q+r)\)
Step-by-step explanation:
\(Factor 30q+5r\\30q+5r\\=5(6q+r)\)
Hope it helps
Ethan claims that StartAbsoluteValue 7 minus 3 EndAbsoluteValue = 4. Which statement about Ethan's claim is true? Ethan is correct because StartAbsoluteValue 7 EndAbsoluteValue = negative 7 and StartAbsoluteValue negative 3 EndAbsoluteValue = 3 so –7 + 3 = 4. Plot –7 on a number line, and move right 3 to get –4 on the line. Ethan is incorrect because StartAbsoluteValue 7 EndAbsoluteValue = 7 and StartAbsoluteValue negative 3 EndAbsoluteValue = 3 so 7 + 3 = 10. Plot 7 on a number line, and move right 3 to get 10 on the line. Ethan is incorrect because the absolute value bars are grouping symbols so first you must subtract. 7 minus 3 = 4, and StartAbsoluteValue 4 EndAbsoluteValue = negative 4. Ethan is correct because the absolute value bars are grouping symbols so first you must subtract. 7 minus 3 = 4, and StartAbsoluteValue 4 EndAbsoluteValue = 4.
Answers
The absolute value of the quantity between the vertical bars is positive
4, which makes Ethan's claim true.
Response:
The true statement is; Ethan is correct because the absolute value bars are grouping symbols so first you must subtract 7 minus 3 = 4 and |4| = 4What are absolute values and how can Ethan's statement be evaluated?Absolute value of a variable x, expressed as |x| is the value of x that is
non negative.
Ethan's claim is expressed as follows; |7 - 3| = 4
The bars of absolute value surrounds the quantity, to which the
magnitude is being referred and the result is always positive not
regarding the sign (positive or negative).
The statement that is true is therefore;
Ethan is correct because the absolute value bars are grouping symbols so first you must subtract 7 minus 3 = 4 and |4| = 4Learn more about absolute values here:
https://brainly.com/question/13153289
Answer: A) Ethan is correct because the absolute value bars are grouping symbols so first you must subtract 7 - 3 = 4, and (4) = 4.
Step-by-step explanation:
Train A and train B leave a central station at the same time. They travel the same speed, but in opposite directions, with train A heading towards station A, and train B heading towards station B. Train A reaches station A after 3 h. Train B reaches station B after 214 h. Station A and Station B are 420 mi apart.
What is the rate of the trains?
Answers
Both the trains A and B have rate of speed at 70 miles per hour.
What is relative speed?Relatve speed is the net speed difference.If they go in same direction we subtract their speeds and if they go in opposite dirtection we add their speed.
According to the given question Train A and Train B has speed of x miles per hour.
As Train A reaches in 3 hours on station A from central station it must be in the middle of station A and station B.
∴ The distance between Train A and station A is half the distance of the distance between station A and station B which is 210 miles.
So, the speed of Train A is (210/3) = 70 miles per hour and as Train B has same speed it is also 70 miles per hour.
learn more about distance and speed here :
https://brainly.com/question/9834403
#SPJ1
There is a bag filled with 6 blue and 5 red marbles.
A marble is taken at random from the bag, the colour is noted and then it is replaced.
Another marble is taken at random.
What is the probability of getting at least 1 blue?
Answers
Answer:
1/11
Step-by-step explanation:
probability =total number of items ÷ 1
=11÷1
=1/11
Section 1
Variability
Which of the following survey question yields data with
Variability? Write Y for yes or N for no.
1) How many bananas did Joe eat yesterday?
2) What is the population of Austin, Texas?
3) What kind of sandwiches does your class like?
4) What is the name of your teacher?
5) How much do televisions cost?
Unlock section 1 by finding the code.
Instructions: Write the answers in order for #1-5. Write Y for yes and
N for no. Use all capitals and no spaces. For example: YYYNN
TA
Answers
Answer:
1) Y
2) Y
3) N
4) N
5) N
steps
1) How many bananas did Joe eat yesterday?
The word "many" tells you that its talking about variability.
2) What is the population of Austin, Texas?
The phrase "What is the population..." tells you that its talking about variability.
3) What kind of sandwiches does your class like?
Doesn't talk about variability.
4) What is the name of your teacher?
Doesn't talk about variability.
5) How much do televisions cost?
Doesn't talk about variability.
(YYNNN)
g a piece of wire 9 m long is cut into two pieces. one piece is bent into a square and the other is bent into an equilateral triangle. (a) how much wire should be used for the square in order to maximize the total area? correct: your answer is correct. m (b) how much wire should be used for the square in order to minimize the total area? incorrect: your answer is incorrect. m
Answers
(a) The length of wire that should be used for the square in order to maximize the total area is 9 meters.
(b) Using the same 9 meters of wire for the square will result in the minimum total area as well as the maximum total area.
(a) To maximize the total area, we need to use as much wire as possible for the square and as little as possible for the triangle. Let x be the length of wire used for the square, then the length of wire used for the triangle is 9 - x.
For the square, we have:
4s = x, where s is the side length of the square.
For the equilateral triangle, we have:
3t = 9 - x, where t is the side length of the equilateral triangle.
Solving for x in terms of s and t, we get:
x = 4s and x = 9 - 3t/2.
Substituting x = 4s into x = 9 - 3t/2, we get:
4s = 9 - 3t/2
8s = 18 - 3t
t = (18 - 8s)/3
The area of the square is given by A = s^2, and the area of the equilateral triangle is given by A = (\(\sqrt{3}\)/4)t^2.
Substituting t = (18 - 8s)/3, we get:
A = (\(\sqrt{3}\)/4)((18 - 8s)/3)^2
To maximize the total area, we need to maximize A, which is a function of s. Taking the derivative of A with respect to s, we get:
dA/ds = -4\(\sqrt{3}\)(4s-9)/27
Setting dA/ds = 0, we get:
4s - 9 = 0
Solving for s, we get:
s = 9/4
Therefore, the length of wire that should be used for the square in order to maximize the total area is:
x = 4s = 9 meters.
(b) To minimize the total area, we need to use as little wire as possible for the square and as much as possible for the triangle. Let x be the length of wire used for the square, then the length of wire used for the triangle is 9 - x.
Using the same equations as in part (a), we get:
t = (18 - 8s)/3
A = (\(\sqrt{3}\)/4)((18 - 8s)/3)^2
Taking the derivative of A with respect to s, we get:
\(dA/ds = -4\sqrt{3}(4s-9)/27\)
Setting dA/ds = 0, we get:
4s - 9 = 0
Solving for s, we get:
s = 9/4
This is the same value as in part (a), which means that using 9 meters of wire for the square will result in the minimum total area as well as the maximum total area.
To know more about total area: https://brainly.com/question/884576
#SPJ11
Find the particular antiderivative of the following derivative that satisfies the given condition. C''(x)=4x2-3x ; C(0)=2000
Answers
The particular antiderivative that satisfies the given condition is: C(x) = (4/9)x^4 - (9/8)x^3 + K1x + 2000
To find the particular antiderivative (or integral) of the given derivative \(C''(x) = 4x^2 - 3x\) that satisfies the condition C(0) = 2000, we need to integrate the given function twice.
First, we integrate C''(x) to find C'(x):
\(C'(x) = ∫ (4x^2 - 3x) dx\)
To find the antiderivative of \(4x^2\), we use the power rule for integration: the power of x increases by 1 and is divided by the new power. Similarly, the antiderivative of -3x is \(-(3/2)x^2\).
\(C'(x) = ∫ (4x^2 - 3x) dx = (4/3)x^3 - (3/2)x^2 + K1\)
Here, K1 is the constant of integration. Next, we integrate C'(x) to find C(x):
\(C(x) = ∫ (C'(x)) dx = ∫ ((4/3)x^3 - (3/2)x^2 + K1) dx\)
To find the antiderivative of \((4/3)x^3\), we again use the power rule for integration. Similarly, the antiderivative of \(-(3/2)x^2\) is \(-(3/2)(1/3)x^3\).
The constant of integration K1 will also be integrated with respect to x, resulting in another constant of integration, K2.
\(C(x) = (1/3)(4/3)x^4 - (1/2)(3/2)x^3 + K1x + K2\)
Simplifying further, we have:
\(C(x) = (4/9)x^4 - (9/8)x^3 + K1x + K2\)
Now, we can apply the initial condition C(0) = 2000 to find the particular solution for K2:
\(C(0) = (4/9)(0)^4 - (9/8)(0)^3 + K1(0) + K2 = 2000\)
Since all the terms involving x become zero when x = 0, we have:
K2 = 2000
Therefore, the particular antiderivative that satisfies the given condition is: \(C(x) = (4/9)x^4 - (9/8)x^3 + K1x + 2000\)
To know more about antiderivative refer here:
https://brainly.com/question/33243567
#SPJ11
solve: log3(x)+log3(x-2)=log3(x+10)
Answers
log3 ( x ) + log3 ( x - 2 ) = log3 ( x + 10 )
log3 ( x )( x - 2 ) = log3( x + 10 )
log3 ( x^2 - 2x ) = log3( x + 10 )
x^2 - 2x = x + 10
x^2 - 3x - 10 = 0
( x - 5 )( x + 2 ) = 0 ==》x = 5 Or x = - 2
you should help meeeee :)
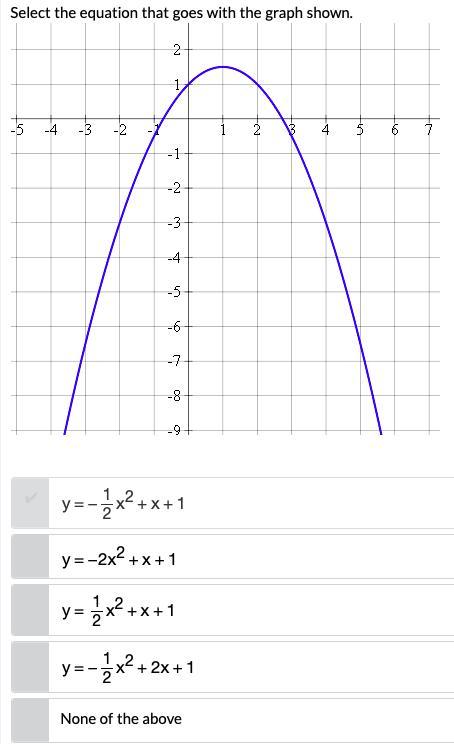
Answers
When we compare this to the options provided, we can see that the equation is: a. y = -x²/2+x+1. The answer is (a) y = -x²/2+x+1.
What is equation of parabola?A parabola's equation can take many different forms, such as vertex form, standard form, or intercept form, depending on its particular shape and orientation.
The parabola's typical vertex form equation is y = a(x - h)² + k
We must locate the vertex form of the parabola in order to get its equation, which is:
y = a(x - h)² + k
Using to determine the vertex
h = -b/2a
To begin, we can locate the vertex:
(-1,0) (1,1.5) (3,0) (-2, -3) (4,-3) (-3,-6) (5,-6)
In order to average the x-values of the two sets of x-intercepts, the vertex must be halfway between the parabola's x-intercepts:
h = (-1 + 3)/2 = 1
The vertex and another point can then be used to find the value of "a":
y = a(x - 1)² + k
Using the point (4, -3):
-3 = a(4 - 1)² + k
-3 = 9a + k
Using the point (1, 1.5):
1.5 = a(1 - 1)² + k
1.5 = k
k = 1.5 is substituted into the second equation:
-3 = 9a + 1.5
-4.5 = 9a
a = -0.5
y = -0.5(x - 1)² + 1.5
When we multiply the equation, we get:
y = -0.5x² + x + 1
To know more about parabola visit:
brainly.com/question/11911877
#SPJ1
Chris rented a truck for one day. There was a base fee of $15.99, and there was an additional charge of 78 cents for each mile driven. Chris had to pay $249.21when he returned the truck. For how many miles did he drive the truck?
Answers
Answer:
299 miles
Explanation:
Base Fee for the truck = $15.99
Charge per mile driven = 78 cents =$0.78
Let the number of miles driven = x
Therefore, for x miles, Chris would be expected to pay a total charge, C defined by the equation below:
\(C=15.99+0.78x\)If Chris had to pay $249.21 when he returned the truck, it means that:
His total charge, C = $249.21
\(\begin{gathered} $249.21$=15.99+0.78x \\ 0.78x=$249.21$-15.99 \\ 0.78x=233.22 \\ \text{Divide both sides by 0.78} \\ x=299 \end{gathered}\)We conclude therefore that Chris drove the truck for 299 miles.
Does anybody know this? An arc has a length of 30 pi feet. Find tge length of the radius if the central angle measured 225

Answers
\(\textit{arc's length}\\\\ s = \cfrac{\theta \pi r}{180} ~~ \begin{cases} r=radius\\ \theta =\stackrel{degrees}{angle}\\[-0.5em] \hrulefill\\ s=30\pi \\ \theta =225 \end{cases}\implies 30\pi =\cfrac{(225)\pi r}{180} \\\\\\ 30\pi (180)=225\pi r\implies \cfrac{30\pi (180)}{225\pi }=r\implies 24=r\)
Please help as Slope is very difficult for me-


Answers
I don't know I just need to answer this so I can get through the login-
Bar chart, help please

Answers
Answer:
the bar charts not being shown properly
in a set of scores with a mean of 100 and a standard deviation of 15, what raw score is represented by a z score of 2.00?a.115b.100c.70d.130
Answers
The raw score represented by a z score of 2.00 is 130 (option d).
What is the raw score corresponding to a z score of 2.00?A z score, also known as a standard score, measures the distance between a particular raw score and the mean of a distribution in terms of standard deviations. In this case, the given set of scores has a mean of 100 and a standard deviation of 15. A z score of 2.00 indicates that the raw score is two standard deviations above the mean.
To find the corresponding raw score, we can use the formula:
Raw Score = (Z Score × Standard Deviation) + Mean
Plugging in the values, we have:
Raw Score = (2.00 × 15) + 100Raw Score = 30 + 100Raw Score = 130Therefore, a z score of 2.00 in this distribution corresponds to a raw score of 130.
Learn more about raw score
brainly.com/question/14927452
#SPJ11
Inductive logical reasoning
1. I see fireflies in my backyard every summer.This summer, I will probably see fireflies in my backyard.
a. Inductive Reasoning
b. Deductive Reasoning
In mathematics, If A = B and B = A
Answers
a. Inductive Reasoning: The statement "I see fireflies in my backyard every summer" is based on observations and generalizing from past experiences.
b. Deductive Reasoning: The statement "If A = B and B = A" is an example of a logical deduction.
a. Inductive Reasoning: The statement "I see fireflies in my backyard every summer" is an example of inductive reasoning. By observing fireflies in the backyard during past summers, a pattern or trend is recognized. This pattern leads to the generalization that fireflies are likely to appear in the backyard during summer. Inductive reasoning involves drawing conclusions based on repeated observations and generalizing from those observations to make a prediction about future events. Therefore, when stating, "This summer, I will probably see fireflies in my backyard," it is an application of inductive reasoning, relying on the assumption that the pattern observed in the past will continue in the future.
b. Deductive Reasoning: The statement "If A = B and B = A" exemplifies deductive reasoning. Deductive reasoning relies on established rules, principles, or premises to draw logical conclusions. In this case, the statement refers to the concept of equality in mathematics. The principle of equality states that if A is equal to B, and B is equal to A, then they are interchangeable and represent the same value. Deductive reasoning allows us to deduce that A and B are equivalent based on the given premise. It involves applying logical reasoning and established principles to arrive at a specific conclusion.
To know more about deductive reasoning, click here: brainly.com/question/2437643
#SPJ11