\(f(x)=(1-0.08)^{\frac{1}{12} } ^{(12t)}\)
my teacher then said from that you get \(f(x)=(0.993)^{12t}\)
can someone explain how you get to this? Please explain this to me I am so confused?
Answers
Answer:
See Below.
Step-by-step explanation:
We have:
\(\displaystyle f(x)=(1-0.08)^{\frac{1}{12}(12t)}\)
First, we can subtract within the parentheses:
\(f(x)=(0.92)^{\frac{1}{12}(12t)}\)
By the properties of exponents:
\(f(x)=((0.92)^\frac{1}{12})^{12t}\)
Approximate. Use a calculator:
\(f(x)\approx (0.993)^{12t}\)
Notes:
0.993 is only an approximation, hence the approximately equal sign.
I'm not given the context of the problem, but it's simpler to just simplify in the exponent like so (the fractions cancel):
\(\displaystyle f(x)=(1-0.08)^{\frac{1}{12}(12t)}=(0.92)^t\)
Full Problem:
The value of Sara's car decreases at a rate of 8% per year.
We will use the exponential decay formula with a set time, given by:
\(f(x)=a(r)^{x/d}\)
Where a is the initial value, r is the rate, x is the time that has passed (dependent on d), and d is the amount of time for one decrease.
For this problem, we can ignore the initial value.
And since the value decreases at a rate of 8% per year, r = 0.92 (we acquire this from 1 - 0.08).
Part 1) Per Month:
Since it decreases per month, d = 12.
\(f(x)=(0.92)^{x/12}\)
Approximate:
\(f(x)=((0.92)^{1/12})^x\approx(.993)^x\)
In this case, x is measured in months.
Part 2) Per Week:
Since it decreases per week, d = 52.
\(f(x)=(0.92)^{x/52}\)
Approximate:
\(f(x)=((0.92)^1/52)^x\approx (.998)^x\)
In this case, x is measured in weeks.
Part 3) Per Day:
So, d = 365.
\(f(x)=(0.92)^{x/365}\)
Simplify:
\(f(x)=((0.92)^{1/365})^x\approx(.999)^x\)
In this case, x is measured in days.
Part 4)
So, as d increases, our r increases as well.
Therefore, the smaller the time interval (from months to weeks to days), the higher our rate of decrease is.
Related Questions
Prove the following statement directly from the definition of divisibility. For all integers a, b, c, and d, if aſc and bld then ab|cd. Proof: Let a, b, c, and d be any integers such that alc and b|d. Then by definition of divisibilityq c= ar and d = bs for some integers r and s. Then cd equals the product of ab and a number that can be written in terms of r and s as follows: cd = ab: , which is an integer because products A of integers are integers. (Simplify your answer completely.) Thus cd = ab · (an integer), and so ablcd by definition of divisibility.
Answers
The cd = ab · (an integer), and so ab | cd by definition of divisibility.
The question wants us to prove the following statement using the definition of divisibility. For all integers a, b, c, and d, if aſc and bld, then ab|cd.Definition of divisibility: Let a and b be integers. We say that b divides a or b is a divisor of a if there exists an integer k such that a = bk.
If b divides a, then we write b | a.Let a, b, c, and d be any integers such that alc and b | d. Then by definition of divisibility, c = ar and d = bs for some integers r and s. Then cd equals the product of ab and a number that can be written in terms of r and s as follows:cd = ab · rs, which is an integer because products of integers are integers.
Learn more about Integer
brainly.com/question/15276410
#SPJ11
The sum of the real numbers x and y is 11. Their differences is 5. What is the value of xy
Answers
John has 8 boxes of apples. Each box holds 10 apples. If 5 of the boxes are full, and 3 of the boxes are half full, how many apples does John have?
Answers
Answer:
65 apples
Step-by-step explanation:
We Know
John has 8 boxes of apples.
Each box holds 10 apples.
If 5 of the boxes are full, and 3 of the boxes are half full, how many apples does John have?
Let's solve
5 boxes are full: 5 x 10 = 50 apples
3 boxes are half full = 3(1/2 · 10) = 15 apples
50 + 15 = 65 apples
So, John has 65 apples.
#11 Find the slope of a line
that passes through the
points (-1, -3) and (-6,5)
Answers
5-(-3)/(-6-(-1))
8/-5
-8/5 is the slope
25°
C
Solve for c.
14
60°
C =
[?
Round your final answer
to the nearest tenth.

Answers
Using Sine rule of Trigonometry, the value of the missing side, c is 28.7
To solve for the missing sides, c, we use the sine rule : The sine rule is related using the formula:
c/ sinC = a / SinA
substituting the values into the formula:
C/sin60° = 14/Sin25
cross multiply
c * sin25 = sin60 * 14
c = (sin60 * 14) / sin25
c = 28.68
Therefore, the value of the side c in the question given is 28.7
Learn more on sine rule :https://brainly.com/question/20839703
#SPJ1
In the diagram below, FG = 10 and HJ =10. Which additional facts would guarantee that FGHJ is a parallelogram
Answers
Answer:
FJ = 15 GH = 15
FG is parallel to HJ
Step-by-step explanation:
Kelly has a rectangular fish aquarium that measures 18 inches long, 8 inches wide, and 12 inches tall. If Kelly wanted to put a protective covering on the four glass walls of the aquarium, how big does the cover have to be
Answers
The protective covering should be 624 square inches. This will cover all four sides of the glass walls of the aquarium. It is the surface area of the aquarium.
Kelly has a rectangular fish aquarium that measures 18 inches long, 8 inches wide, and 12 inches tall.
If Kelly wanted to put a protective covering on the four glass walls of the aquarium, how big does the cover have to be?
A protective covering on the four glass walls of the aquarium can be equated to the surface area of the glass walls.
The aquarium is rectangular, and thus has two identical sides that are 12 inches tall and 8 inches wide each, and two identical sides that are 12 inches tall and 18 inches long each.
Hence, the surface area of the glass walls of the aquarium is
Area = 2 × (length × height) + 2 × (width × height)
= 2 × (18 × 12) + 2 × (8 × 12) = 432 + 192
= 624
Therefore, the protective covering should be 624 square inches.
This will cover all four sides of the glass walls of the aquarium. It is the surface area of the aquarium.
Learn more about aquarium from the given link
https://brainly.com/question/28889858
#SPJ11
Identify the vertex of the quadratic function y = 4x² − 16x + 3. Be sure to show all the steps in your work, whether you complete the square or you use a formula to find the vertex.
Answers
The vertex of the quadratic function y = 4x² − 16x + 3 can be found using the formula x = -b / (2a), where a, b, and c are the coefficients of the quadratic equation.
To find the vertex of the quadratic function y = 4x² − 16x + 3, we can either complete the square or use the formula for the vertex. I'll show you both methods:
Method 1: Completing the square
Step 1: Start with the quadratic function in standard form: y = ax² + bx + c.
In our case, a = 4, b = -16, and c = 3.
Step 2: Divide the coefficient of x by 2 and square the result. Add this value and subtract it inside the parentheses. Add or subtract the same value outside the parentheses to maintain the equality.
To complete the square, we need to consider the coefficient of x, which is -16.
(-16/2)² = (-8)² = 64
So we can rewrite the equation as:
y = 4x² − 16x + 3
= 4(x² − 4x + 4 - 4) + 3
= 4(x² − 4x + 4) - 16 + 3
= 4(x - 2)² - 13
Step 3: The vertex of the parabola is given by the values (h, k), where h and k are the coordinates of the vertex. In our case, the vertex form of the equation is y = a(x - h)² + k.
Comparing this to the equation we derived in step 2, we can see that the vertex is (2, -13).
Method 2: Using the vertex formula
The vertex of a quadratic function in the form y = ax² + bx + c can be found using the vertex formula:
h = -b / (2a)
k = f(h)
In our equation, a = 4 and b = -16. Plugging these values into the formulas, we have:
h = -(-16) / (2 * 4)
= 16 / 8
= 2
To find k, we substitute the value of h back into the original equation:
k = 4(2)² − 16(2) + 3
= 4(4) - 32 + 3
= 16 - 32 + 3
= -13
Therefore, the vertex of the quadratic function y = 4x² − 16x + 3 is (2, -13).
Both methods yield the same result: the vertex of the parabola is at the point (2, -13).
Learn more about quadratic function here:
https://brainly.com/question/30929439
#SPJ11
Find the area.
4m
6m
6m

Answers
what is the probability that a photon with the polatization state you just calculated will be transmitted through a subsequent filter, that is aligned with the h direction.
Answers
The maximum probability that a photon with the polarization state will be transmitted through the A filter is 1/2
To solve this problem, we need to use Malus' law, which states that the intensity of light transmitted through a polarizer is proportional to the square of the cosine of the angle between the polarization direction of the incoming light and the axis of the polarizer.
To find the overall probability that a photon will be transmitted through all three filters, we need to multiply the probabilities of each filter
P = 1/2 × cos²(θ) × 1
We are not given the angle θ, so we cannot calculate the exact value of P. However, we can calculate the maximum value of P, which occurs when the rotated filter is aligned with the A filter (i.e., θ = 0). In this case, P = 1/2.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
The given question is incomplete, the complete question is:
H filter Rotated filter Rotated filter followed by A filter An unpolarized photon beam is incident on a linear polarizing filter. The incoming photon flux is is 2.34 x 101 photons/m' /sec. What is the probability that a photo with the polarization state be transmitted through a subsequent filter, that is aligned with the direction?
HELP ASAP
10. A store is selling its display furniture at a discount of 35%. How much would be paid for
a chair regularly selling for $195.95 if sales tax is 8%?
Answers
What is the common difference of the arithmetic sequence? 2,5,8,11,14...
Answers
The common difference is 3.
14-11=3
11-8=3
8-5=3
5-2=3
You can see here that the difference between two consecutive numbers in this sequence are all 3.
difference = 3
i hope that’s correct!!!
Seven hours were allotted for a trip. If Saul's average speed was 65 miles per hour
how far could he go in the allotted time
Answers
Answer:
455 mph (miles per hour)
Step-by-step explanation:
65 x 7 = 455
Sorry if it is short. I wanna get as much answers before Exam Mode starts.
5000 containers are stacked 20 wide and 50 long on a ship. How many containers high are they? Pls answer and give explanation, thx
Answers
Answer:
5 containers high
Step-by-step explanation:
Given that :
Given :
Width = 20 containers
Length = 50 containers
Total containers = 5000
Hence,
Total containers = width * length * height
5000 = 20 * 50 * height
5000 = 1000 * height
Height = 5000 / 1000
Height = 5 containers
Çok acil arkadaşlar lütfen

Answers
Answer:
Step-by-step explanation:
A 25-year-old woman burns 550t cal/hr while walking on her treadmill. How many calories are burned after walking for 4 hours? calories burned
Answers
The woman burned 2,200 calories after walking for 4 hours on her treadmill.
Determine the calories burned?Given that the woman burns 550 calories per hour while walking on her treadmill, we can calculate the total calories burned by multiplying the calories burned per hour by the number of hours walked.
Calories burned per hour = 550 cal/hr
Number of hours walked = 4 hours
Total calories burned = Calories burned per hour × Number of hours walked
= 550 cal/hr × 4 hours
= 2,200 calories
Therefore, the woman burned 2,200 calories after walking for 4 hours on her treadmill.
To know more about calories, refer here:
https://brainly.com/question/22374134#
#SPJ4
Find the flow rate of water in each (steel) pipe at 25°C in each
pipe. Ignore minor losses.
1.2 ft³/s All pipes 2-1/2-in Schedule 40 50 ft 50 ft 30 ft 50 ft 50 ft 0.3 ft³/s 0.3 ft³/s 30 ft 0.6 ft³/s
Answers
The flow rate of water in each steel pipe at 25°C is as follows:
Pipe 1: 1.2 ft³/s
Pipe 2: 0.3 ft³/s
Pipe 3: 0.3 ft³/s
Pipe 4: 0.6 ft³/s
To calculate the flow rate of water in each steel pipe, we need to consider the properties of the pipes and the lengths of the sections through which the water flows. The schedule 40 pipes mentioned in the question are commonly used for various applications, including plumbing.
Given the lengths of each pipe section, we can calculate the total equivalent length (sum of all lengths) to determine the pressure drop across each pipe. Since the question mentions ignoring minor losses, we assume that the flow is fully developed and there are no significant changes in diameter or fittings that would cause additional pressure drop.
Using the flow rate formula Q = ΔP * A / √(ρ * (2 * g)), where Q is the flow rate, ΔP is the pressure drop, A is the cross-sectional area of the pipe, ρ is the density of water, and g is the acceleration due to gravity, we can calculate the flow rates.
Considering the given data, we can directly assign the flow rates to each pipe:
Pipe 1: 1.2 ft³/s
Pipe 2: 0.3 ft³/s
Pipe 3: 0.3 ft³/s
Pipe 4: 0.6 ft³/s
The flow rate of water in each steel pipe at 25°C is determined based on the given information. Pipe 1 has a flow rate of 1.2 ft³/s, Pipe 2 and Pipe 3 have flow rates of 0.3 ft³/s each, and Pipe 4 has a flow rate of 0.6 ft³/s. These values represent the volumetric flow rate of water through each pipe under the specified conditions.
To know more about flow rate visit:
https://brainly.com/question/31070366
#SPJ11
Consider the enlargement of the triangle.
A small triangle has a base of 1.7 feet and height of 9.3 feet. A larger triangle has a base of 3.5 feet and height of x feet.
Not drawn to scale
Rounded to the nearest tenth, what is the value of x?
15.8 feet
19.1 feet
23.3 feet
32.6 feet
Answers
Answer:B 19.1 feet
Step-by-step explanation:
The value of the x is 19.1 feet.
What is ratio?"It is an ordered pair of numbers a and b, written \(\frac{a}{b}\) where b does not equal 0."
What is proportion?"When two ratios are equal then they are said to be in proportion."
For given question,
A small triangle has a base of 1.7 feet and height of 9.3 feet.
A larger triangle has a base of 3.5 feet and height of x feet.
Since it is the enlargement of the triangle, the sides of both the triangle must be in proportion.
\(\Rightarrow \frac{1.7}{3.5}= \frac{9.3}{x}\\\\\ \Rightarrow 1.7\times x=3.5\times 9.3\\\\ \Rightarrow 1.7\times x=32.55\\\\ \Rightarrow x=19.14\)
Therefore, the value of the x is 19.1 feet.
Learn more about the ratio and proportion here:
https://brainly.com/question/26974513
#SPJ2
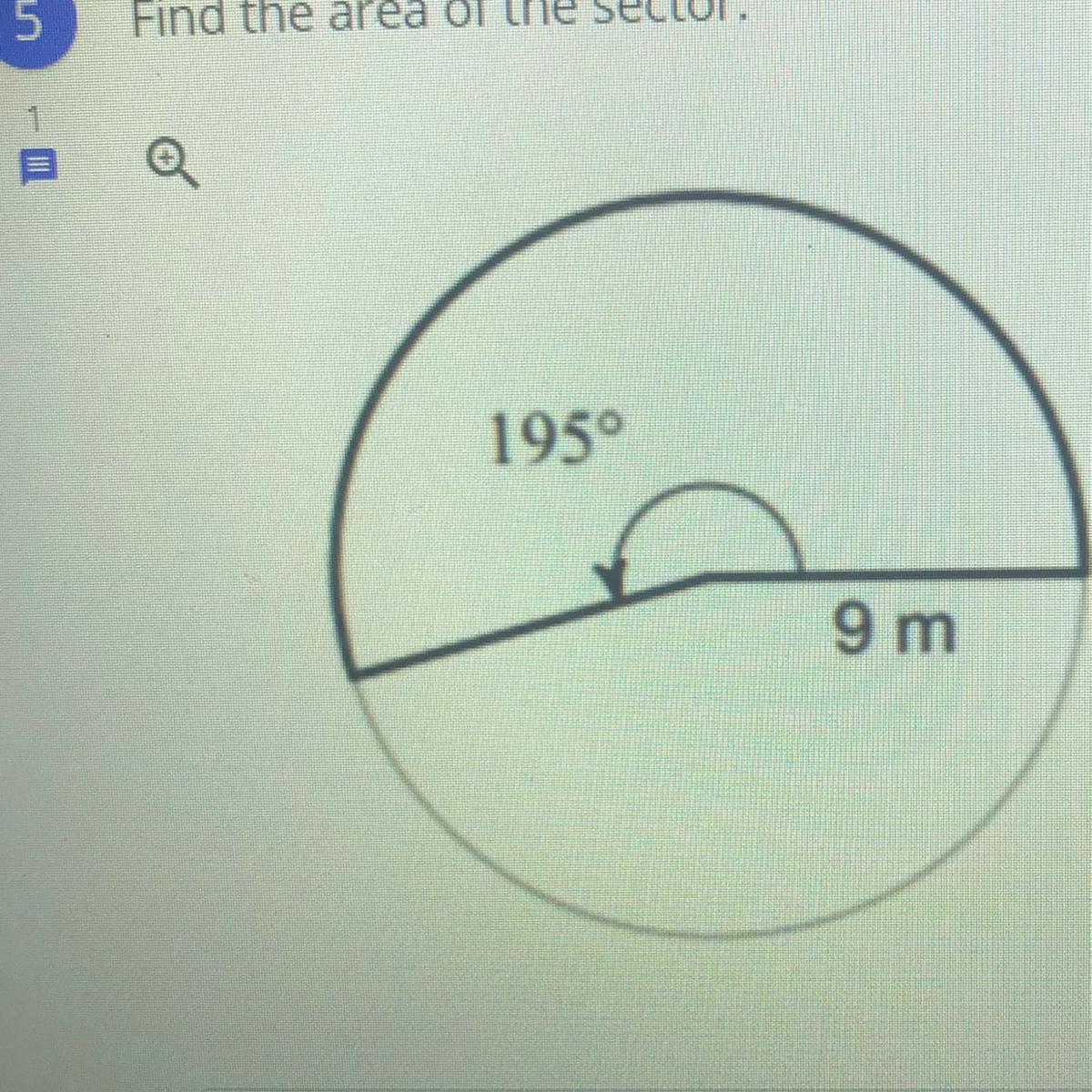
Find the area of the sector.
195°
9 m
Answers
Answer:B
Step-by-step explanation: Because it right
I lowered the points because people were stealing them.

Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
Domain ~
\( - 6 \leqslant x \leqslant - 1\)Range ~
\( - 5 \leqslant x \leqslant - 3\)a researcher wishes to estimate within $300 the true average amount of money a county spends on road repairs each year. if she wants to be 90% confident, how large a sample is necessary? the standard deviation is known to be $900.
Answers
The sample size should be 24.
What is the sample size?
The process of deciding how many observations or replicates to include in a statistical sample is known as sample size determination. Any empirical study with the aim of drawing conclusions about a population from a sample must take into account the sample size as a crucial component.
Here, we have
Given
Margin of error = 300
confidence level = 0.9
standard deviation = 900
Assuming the standard deviation to be of population
ME = Z(0.1/2) × σ/√n
300 = 1.645 × 900/√n
n = {(1.645 × 900)300}²
n = 24
Hence, the sample size should be 24.
To learn more about the sample size from the given link
https://brainly.com/question/24158610
#SPJ4
identify three strategies that the federal government could implement to encourage the use of bevs. assume that the fuel efficiency of the ice vehicle is 235 miles per gallon and that gasoline costs $3.75 per gallon.calculate the cost of gasoline per mile.
Answers
Three strategies that implement to encourage the use of BEVs are incentives, Infrastructure and Regulations. The cost of gasoline per mile for an ICE vehicle is $0.016 per mile.
Incentives: The federal government could offer financial incentives such as tax credits, rebates, or grants to consumers who purchase BEVs. This would make BEVs more affordable and help to offset the higher upfront cost of these vehicles.
Infrastructure development: The federal government could invest in the development of charging infrastructure for BEVs, such as public charging stations. This would help to alleviate range anxiety and make BEVs more convenient and practical for consumers.
Regulations: The federal government could implement regulations that incentivize or require automakers to produce more BEVs. This could include emissions standards that are more favorable to BEVs, or mandates for automakers to produce a certain percentage of their vehicles as electric.
To calculate the cost of gasoline per mile for an ICE vehicle with fuel efficiency of 235 miles per gallon and gasoline cost of $3.75 per gallon, we divide the cost of gasoline by the fuel efficiency:
Cost per mile = $3.75 / 235 miles per gallon
Cost per mile = $0.016 per mile
To learn more about cost click on,
https://brainly.com/question/24357861
#SPJ4
Evaluate the integral do I = a+cosd' (a) if a > 1; (b) if a=ao+ie, where ao and e are real and positive. Assume that do
Answers
a. the integral \(I\) becomes \(\[I = a\theta + \sin(\theta) + C\]\) where \(\(C\)\) is the constant of integration. b. the integral \(I\) becomes \(\[I = \frac{1}{2}a\theta^2 + \sin(\theta) + C\]\) where \(\(C\)\) is the constant of integration.
To evaluate the integral \(I = \int (a + \cos(\theta)) \, d\theta\), we can apply the integral rules and properties. Let's consider the two given cases:
(a) If \(a > 1\):
In this case, the integral can be evaluated directly. The integral of \(a\) with respect to \(\theta\) is \(a\theta\), and the integral of \(\cos(\theta)\) is \(\sin(\theta)\). Therefore, the integral \(I\) becomes:
\[I = a\theta + \sin(\theta) + C\]
where \(C\) is the constant of integration.
(b) If \(a = a_0 + i e\), where \(a_0\) and \(e\) are real and positive:
In this case, the integral can also be evaluated using the same rules. The integral of a constant multiplied by a variable is \(\frac{1}{2}a\theta^2\), and the integral of \(\cos(\theta)\) is \(\sin(\theta)\). Therefore, the integral \(I\) becomes:
\[I = \frac{1}{2}a\theta^2 + \sin(\theta) + C\]
where \(C\) is the constant of integration.
It's important to note that the integral is evaluated based on the assumption that \(d\theta\) is the differential of \(\theta\) and not a different variable. Also, \(C\) represents the constant of integration, which can take any value.
Learn more about integral here
https://brainly.com/question/30094386
#SPJ11
A line passes through the point (6, - 3) and has a slope of -2.
Write an equation in slope-Intercept form for thls line.
Answers
To find the equation of the line passing through the point (6, -3) with a slope of -2, we can use the point-slope form of the equation of a line:y - y1 = m(x - x1)where (x1, y1) is the given point and m is the slope.Substituting the given values, we get:y - (-3) = -2(x - 6)Simplifying, we get:y + 3 = -2x + 12Subtracting 3 from both sides, we get:y = -2x + 9So, the equation of the line is y = -2x + 9
Which statement is false?
O A. Every integer is also a rational number.
O B. Every rational number is also an integer.
O C. Every irrational number is also real.
O D. No rational number is irrational.
Answers
A triangle on the coordinate plane has points located at A (2,5), B (5,9), and C (8,5). What is the area of the triangle? O A 10 square units O B. 24 square units O C 12 square units O D. 8 square units
Answers
What’s the circumference?

Answers
Answer:
C=2πr=2·π·4≈25.13274
Step-by-step explanation:
Answer:
The formula to get the circumference of a circle is \(C=2*\pi * r\). We can then input the value and we get that \(C=2*\pi*4\) and as we solve it more the final answer that we get is \(C=25.133\).
Hope this helps! Let me know if you have any questions
express the integral as a limit of riemann sums. do not evaluate the limit. (use the right endpoints of each subinterval as your sample points.) ∫ 8 4 x 1 x 3 d x ∫48x1 x3dx
Answers
Thus, the limit is the definition of the definite integral ∫8^4 x/(x^3) dx, expressed as a limit of Riemann sums with right endpoints.
To express the integral ∫8^4 x/(x^3) dx as a limit of Riemann sums, we first need to partition the interval [4,8] into n subintervals of equal width Δx = (8-4)/n.
Let xi be the right endpoint of the ith subinterval, so xi = 4 + iΔx.
Then, the Riemann sum with right endpoints is:
∑(i=1 to n) f(xi)Δx
where f(xi) is the value of the function x/(x^3) at xi.
Substituting xi = 4 + iΔx and f(xi) = xi/(xi^3), we get:
∑(i=1 to n) (4+iΔx)/(4+i^3Δx^3) Δx
This is the expression for the Riemann sum with right endpoints.
To express the integral as a limit of Riemann sums, we take the limit of this expression as n goes to infinity:
lim(n->∞) ∑(i=1 to n) (4+iΔx)/(4+i^3Δx^3) Δx
This limit is the definition of the definite integral ∫8^4 x/(x^3) dx, expressed as a limit of Riemann sums with right endpoints.
Know more about the limit of Riemann sums
https://brainly.com/question/30241844
#SPJ11
2. The following set of count readings was made in a gradient-free γ-ray field, using a suitable detector for repetitive time periods of one minute: 18,500;18,410; 18,250;18,760;18,600;18,220;18,540;18,270;18,670;18,540. (a) What is the mean value of the number of counts? (b) What is its standard deviation (S.D.)? (c) What is the theoretical minimum S.D. of the mean? (d) What is the actual S.D. of a single reading? (e) What is the theoretical minimum S.D. of a single reading?
Answers
The inflection point of f(t) is approximately t = 3.73.
(a) To determine if the function f(t) = -0.425t^3 + 4.758t^2 + 6.741t + 43.7 is increasing or decreasing, we need to find its derivative and examine its sign.
Taking the derivative of f(t), we have:
f'(t) = -1.275t^2 + 9.516t + 6.741
To determine the sign of f'(t), we need to find the critical points. Setting f'(t) = 0 and solving for t, we have:
-1.275t^2 + 9.516t + 6.741 = 0
Using the quadratic formula, we find two possible values for t:
t ≈ 0.94 and t ≈ 6.02
Next, we can test the intervals between these critical points to determine the sign of f'(t) and thus the increasing or decreasing behavior of f(t).
For t < 0.94, choose t = 0:
f'(0) = 6.741 > 0
For 0.94 < t < 6.02, choose t = 1:
f'(1) ≈ 14.982 > 0
For t > 6.02, choose t = 7:
f'(7) ≈ -5.325 < 0
From this analysis, we see that f(t) is increasing on the intervals (0, 0.94) and (6.02, ∞), and decreasing on the interval (0.94, 6.02).
(b) To find the inflection point of f(t), we need to find the points where the concavity changes. This occurs when the second derivative, f''(t), changes sign.
Taking the second derivative of f(t), we have:
f''(t) = -2.55t + 9.516
Setting f''(t) = 0 and solving for t, we find:
-2.55t + 9.516 = 0
t ≈ 3.73
Therefore, The inflection point of f(t) is approximately t = 3.73.
Learn more about inflection point here:
https://brainly.com/question/29249123
#SPJ11
PLS HELP ASAP ILL GIVE BRAINLKEST PLS THANKS ASAP

Answers
Answer:
A.
they choose candidates before the general election