The Regression Equation Suppose in this semester, our Exam 1 average was about 91 with an SD of about 10.5. Suppose the correlation between our Exam 1 and Exam 2 scores will be similar to what it has been in the past, about 0.75, and finally, suppose our Exam 2 scores will be similar to previous semesters Exam 2 scores with an average of 85 and a SD of 8.2. Use this information
1. What the slope of the regreso equation for predicting our Exam 2 scores from Exam 1 scores Round to 3 decimal places Tries 0/5
2. What the yntercept of the regression ecuation for predicting our team scores from Exam 1 scores found to 3 decimal places Tres 0/5
3. A student got a 96 on our Exam 1 Use the regression equation you just calculated to predict her Exam 2 score (round to the rounds to 29.) rest whole number. For example, 79.5 rounds to 80, n . But 79.49 Tres 0/5
4. Another student got a 65 on Fram 1. What would you predict her Exam 2 score to be? Round your answer to the nearest whole num
5. What is the SD of the prediction errors (same as RMSE) of our regression ecuation Round to 2 decimal places.
Answers
Answer:
1. Slope = 0.5857
2. Intercept = 31.7
3. Y = 88
4. X = 70
5. 5.4234
Step-by-step explanation:
We have x and y
Mean of x = 91
Mean of y = 85
Sd of x = Sx = 10.5
Sd of y = Sy = 8.2
The registration regression equation
Y - ybar = r(Sy/Sx)(x-xbar)
y - 85 = 0.75(8.2/10.5)(x-91)
Y - 85 = 0.75(0.7809)(x-91)
Y-85 = 0.5857X - 53.3
Y = 0.5857X - 53.3+85
Y = 0.5857X + 31.7
1. Slope = 0.5857
2. Intercept = 31.7
3. If x = 96,
Y = 0.5857(96) + 31.7
Y = 87.927
Y = 88
4. If x = 65,
Y = 0.5857(65)+31.7
Y = 69.77
Y = 70
5. Sy * √(1-r²)
= 8.2 x √(1-0.75²)
= 8.2 x √(1-0.5625
8.2 x √0.4375
= 8.2x 0.6614
= 5.4234
Related Questions
If p = 14, r = -7, and s = -4, find q.
Answers
Answer:
quesadillas
Step-by-step explanation:
Please someone help and explain them to me. im confused




Answers
is there a way i can draw on it to help explain it?
on Monday a local hamburger shop sold a combined total of 375 hamburgers and cheese burgers. the number of cheeseburgers sold was two times the number of hamburgers sold.how many hamburgers were sold?
Answers
Answer =
Equations:
Quantity Eq. : h + c = 375
Quantity Eq. : c = 3h
----------------------------
Substitute to solve for "h":
h + 2h = 375
3h = 375
h = 125 (# of hamburgers)
----------
Substitute to solve for "c":
125 + c = 375
c = 250 (# of cheeseburgers)
Of all the Sunny Club members in a particular city, 25% prefer swimming on weekends and 75% prefer swimming on weekdays. It is found that 20% of the members in that city prefer swimming on weekends and are female, while 55% of the members in that city prefer swimming on weekdays and are female.
The probability that a club member picked randomly is female, given that the person prefers swimming on weekends, is_____.
P = Desired outcomes divided by the total outcomesm me
Answers
Answer:
The probability that a club member picked randomly is female, given that the person prefers swimming on weekends, is 0.8 = 80%.
Step-by-step explanation:
We use the conditional probability formula to solve this question. It is
\(P(B|A) = \frac{P(A \cap B)}{P(A)}\)
In which
P(B|A) is the probability of event B happening, given that A happened.
\(P(A \cap B)\) is the probability of both A and B happening.
P(A) is the probability of A happening.
In this question:
Event A: Prefers swimming on weekends.
Event B: Being female.
25% prefer swimming on weekends
This means that \(P(A) = 0.25\)
It is found that 20% of the members in that city prefer swimming on weekends and are female
This means that \(P(A \cap B) = 0.2\)
So
\(P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{0.2}{0.25} = 0.8\)
The probability that a club member picked randomly is female, given that the person prefers swimming on weekends, is 0.8 = 80%.
1)
Science 5
Measurement Assignment
Name each measurement instrument below. Then, indicate which
type of measurement is performed with each one. Remember,
some instruments can be used for more than one type of
measurement!
Instrument
Name of Instrument
Measurement Type

Answers
Answer: See below
Step-by-step explanation:
The first is a beaker, it's used to measure liquid volume
The second is a ruler, it's used to measure length.
Last is a thermometer, it's used to measure temperature.
Mr. Cole made this diagram of his bedroom. Which is the area of Mr. Cole’s bedroom? 90 square feet 82 square feet 72 square feet 36 square feet

Answers
Answer:
The answer is 82 square feet
Step-by-step explanation:
An easy way to do this is to split it into two rectanlges. You can do 10*5 and 8*4 as the dimensions to the two rectangles or you can do 2*4 and 9*8.
I am going to do the first option.
The area of a rectangle is length times width.
Rectangle one can be the one with the dimensions 10 and 5 and the length and width.
Rectangle two can be the one with the dimensions 8 and 4 and the length and width.
Area of rectangle one = 50 feet^2
Area of rectangle two = 32 feet^2
Since we split a large irregular shape into two bits, we must add them together, which results in 82 feet^2.
In the diagram, the measures of 23 and 27 are 45°. The measure of 25 is
135°. Are lines cand dparallel?
F
5
8
OA. Yes, because 23 and 27 are congruent.
OB. No, because 27 and 25 are not congruent.
C. Yes, because 25 and 27 are supplementary.
D. No, because 23 and 25 are not supplementary.
Answers
The correct answer is D. No because 23 and 25 are not supplementary.
In the given diagram, it is stated that the measures of angles 23 and 27 are 45°, and the measure of angle 25 is 135°. To determine if lines C and D are parallel, we need to analyze the angles formed by these lines.
If the alternate interior angles or corresponding angles are congruent, then the lines are parallel. However, in this case, we don't have enough information about the angles formed by lines C and D to make that determination.
The fact that angle 23 and angle 27 are congruent (both measuring 45°) doesn't provide any information about the relationship between lines C and D. Similarly, the measure of angle 25 being 135° doesn't give us any insight into the parallelism of lines C and D. Therefore, we cannot conclude that lines C and D are parallel based on the given information, and the correct answer is D.
For more such answers on supplementary angle
https://brainly.com/question/12919120
#SPJ8
The director of a state agency believes that the average starting salary for clerical employees in the state is less than $30,000 per year. To test her hypothesis, she has collected a random sample of 100 starting clerical salaries from across the state and found that the sample mean is $29,750. a) Develop the appropriate null and alternative hypotheses. b) Assuming the standard deviation is known to be $2,500 and the significance level for the test is to be 0.05, what is the t-statistic
Answers
Answer:
The test statistics is \(z = -1\)
Step-by-step explanation:
From the question we are told that
The sample size is n = 100
The null hypothesis is \(H_o : \mu = \$30000\)
The alternative hypothesis is \(H_a : \mu < \$ 30000\)
The sample mean is \(\= x = \$29,750\)
The standard deviation is \(\sigma = \$2,500\)
The level of significance is \(\alpha =0.05\)
Generally the test statistics is mathematically represented as
\(z = \frac{\= x - \mu }{ \frac{ \sigma}{ \sqrt{n} } }\)
=> \(z = \frac{29750 - 30000 }{ \frac{ 2500}{ \sqrt{100} } }\)
=> \(z = -1\)
From the desired test, we have that:
a)
The null hypothesis is: \(H_0: \mu \geq 30000\)The alternative hypothesis is: \(H_1: \mu < 30000\)b) The t-statistic is t = -1.
Item a:
At the null hypothesis, we test if the average starting salary for clerical employees in the state is not less than $30,000, that is:
\(H_0: \mu \geq 30000\)
At the alternative hypothesis, it is tested if the salary is less than $30,000, that is:
\(H_1: \mu < 30000\)
Item b:
We have the standard deviation for the sample, thus, the t-distribution is used. The test statistic is given by:
\(t = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}\)
The parameters are:
\(\overline{x}\) is the sample mean. \(\mu\) is the value tested at the null hypothesis. s is the standard deviation of the sample. n is the sample size.For this problem, the values of the parameters are: \(\overline{x} = 29750, \mu = 30000, s = 2500, n = 100\)
Hence, the t-statistic is:
\(t = \frac{\overline{x} - \mu}{\frac{s}{\sqrt{n}}}\)
\(t = \frac{29750 - 30000}{\frac{2500}{\sqrt{100}}}\)
\(t = -1\)
The t-statistic is t = -1.
A similar problem is given at https://brainly.com/question/13873630
WHAT IS DA POINT OF LIFE
Answers
Differentiate y=x4 -x
Answers
Answer:
Step-by-step explanation:
To differentiate the function y = x^4 - x, we will use the power rule of differentiation. The power rule states that if f(x) = x^n, then the derivative of f(x) is f'(x) = nx^(n-1).
So, for y = x^4 - x, we can find the derivative as follows:
y' = 4x^3 - 1
So, the derivative of the function y = x^4 - x is y' = 4x^3 - 1.
Compute the monthly payments for the add on interest loan. The amount of the loan is $8,276.17. The annual interest rate is 5.7%. The term of the loan is 5.5 years.
Answers
The monthly payments for this add on interest loan are of $164.71.
Given Information and Formula Used
It is given that for an add on interest loan,
Principal Amount, p = $8,276.17
Annual Interest Rate, r = 5.7%
Term of the loan, T = 5.5 years
The formula for simple interest is given as follows,
I = (p)(r)(t)/100 ............... (1)
The formula for total amount of add on interest is given by,
A = p + I ....................... (2)
Computing the Interest
Substitute the given values of p, r, and t in the formula (1) of interest to get,
I = (8276.17)(5.7)(5.5)/100
I = 259457.9295/100
I = $2,594.58
Computing the Monthly Payment for Add-on Interest Loan
Substituting the values of p and I in the formula (2), we obtain the total amount as,
A = $ (8276.17 + 2594.58)
A = $ 10,870.75
Monthly payment for the add on interest loan = A/t(in months)
= $ (10,870.75/66)
= $164.71
Therefore, monthly payments of $164.71 are to be made for the add on interest loan.
Learn more about interest here:
https://brainly.com/question/26457073
#SPJ1
Medical researchers are studying a certain genetic trait found in two populations of people, W and X. From an independent random sample of people taken from each population, the difference between the sample proportions of people who carried the trait (W minus X) was 0.22. Under the assumption that all conditions for inference were met, a hypothesis test was conducted using the following hypotheses.
H0 : pW=pXHa : pW > p XHo : pW= pX Ha: pW >pX
The p-value of the test was 0.03. Which of the following is the correct interpretation of the p-value?
a. The probability of selecting a person from population W who carries the trait is 0.22, and the probability of selecting a person from population X who carries the trait is 0.03.
b. If the proportions of all people who carry the trait are the same for both populations, the probability of observing a sample difference of at least 0.22 is 0.03.
c. If the proportions of all people who carry the trait are the same for both populations, the probability of observing a sample difference of 0.22 is 0.03.
d. If the difference in proportions of people who carry the trait between the two populations is actually 0.22, the probability of observing that difference is 0.03.
e. If the difference in proportions of people who carry the trait between the two populations is actually 0.03, the probability of observing that difference is 0.22.
Answers
Answer:
If the proportions of all people who carry the trait are the same for both populations, the probability of observing a sample difference of at least 0.22 is 0.03
Step-by-step explanation:
Given the hypothesis :
H0 : pW = pX
Ha : pW > pX
W - X = 0.22
Pvalue = 0.03
Since the Pvalue gives the probability of obtaining a value or result figure which is atleast as extreme as the observed value. The observed value here is 0.22 resulting from the difference in W and X (W - X).
This can thus be interpreted to mean ; going by the Null (difference between W and X) ; the probability of obtaining a value of atleast 0.22 as difference is 0.03
Mrs. Girard bought a 2-ounce tube of eye cream. Each night, she carefully applies 0.1
ounces.
Write an equation that shows how the number of ounces of eye cream remaining, y, depend
on the number of nights Mrs. Girard uses it, X.
y =
Answers
I HOPE THIS HELPS
Solve for p.
4p + 2 ≤ 10
Answers
Answer:
p=2
Step-by-step explanation:
4p+2≤10
-2 -2
4p≤8
divide by 4
p≤2
Answer:
p ≤ 2
Step-by-step explanation:
Point A is located at (1, 2). Point B is located at (4, 6). Use this information to determine the length of the line, rounded to the nearest whole number.
Answers
If Point A is located at (1, 2) and Point B is located at (4, 6), the length of the line between points A and B is 5 units.
To determine the length of the line between points A and B, we can use the distance formula, which is a formula used to calculate the distance between two points in a coordinate plane. The distance formula is:
d = √((x₂ - x₁)² + (y₂ - y₁)²)
where (x₁, y₁) and (x₂, y₂) are the coordinates of the two points and d is the distance between them.
Using the coordinates of points A and B, we can substitute their values into the distance formula to find the length of the line between them:
d = √((4 - 1)² + (6 - 2)²)
d = √(3² + 4²)
d = √(9 + 16)
d = √25
d = 5
Rounded to the nearest whole number, the length of the line is also 5 units.
In conclusion, we can use the distance formula to find the length of the line between two points in a coordinate plane. The distance formula uses the coordinates of the two points to calculate the distance between them. The resulting distance can be rounded to the nearest whole number, if needed.
To learn more about distance click on,
https://brainly.com/question/28658621
#SPJ1
What is the volume of a rectangular prism with a length of 12ft, a width of 10ft, and a height of 18ft?
Answers
Answer:
2160ft³
Step-by-step explanation:
V=whl=10·18·12=2160ft³
your friend earns $10 babysitting. This is 3 more than you earn for washing the car. How much do you make for washing the car
Answers
Answer:
$7
Step-by-step explanation:
$10 - $3 = $7
(PHOTO) please help need this done by tomorrow thank you.

Answers
Answer: 125
Step-by-step explanation: ∠4 and 55 are supplementary angles. This means that ∠4 and 55 add up to 180. We can use this to solve for ∠4.
180 - 55 = ∠4
125 = ∠4
So, ∠4 is equal to 125 degrees.
Would appreciate brainly <3
Harley is riding her bicycle 9.6 miles from her house to work. If she rides at a speed of 15 miles per hour, how long will it. Take Harley to arrive at work
Answers
Answer:
she will arrive at her work in approximately 38.4 minutes
Step-by-step explanation:
you divide her mph by 60 to see how fast she is traveling per minute. she traveled .25 miles per minute. you divide the total distance she is biking by the distance she travels per minute.
15/60=0.25
9.6/0.25= 38.4
G (x) = x^2 - 3x + 2 , find g (-4) - show work
Answers
Answer:
30
Step-by-step explanation:
Plug in -4 wherever you see an x. So:
(\(-4^{2}\))-(3*-4)+2 --> (16) - (-12) + 2 --> 16 + 12 +2 (two negatives make a positive) --> 28 + 2 = 30
Which systems of equations have the same solutions?
L (3x+y = 8
1x - 4y = -6
m{$*=*=230
NS 4x – 3y = 2
12% -8y = -12

Answers
Answer:
B. L and N
Step-by-step explanation:
Let's solve each system
✔️System L:
3x + y = 8 => Eqn. 1
x - 4y = -6 => Eqn. 2
x = -6 + 4y
Substitute x = (-6 + 4y) in eqn. 1
3(-6 + 4y) + y = 8
-18 + 12y + y = 8
-18 + 13y = 8
13y = 8 + 18
13y = 26
y = 26/13
y = 2
Substitute y = 2 into Eqn. 2
x - 4y = -6
x - 4(2) = -6
x - 8 = -6
x = -6 + 8
x = 2
Solution to system L = (2, 2)
✔️System M:
4x - 3y = 2 => Eqn. 1
5x - 4y = -30 => Eqn. 2
Multiply eqn 1 by 5, and eqn. 2 by 4
20x - 15y = 10
20x - 16y = -120
Subtract
y = 130
Substitute y = 130 into eqn. 1
4x - 3(130) = 2
4x - 390 = 2
4x = 2 + 390
4x = 392
x = 392/4 = 98
Solution to system M = (98, 130)
✔️System N:
4x - 3y = 2 =>Eqn. 1
2x - 8y = -12 => Eqn. 2
Multiply Eqn. 1 by 2, and eqn. 2 by 4
8x - 6y = 4
8x - 32y = -48
Subtract
26y = 52
y = 52/26
y = 2
Substitute y = 2 into eqn. 1
4x - 3(2) = 2
4x - 6 = 2
4x = 2 + 6
4x = 8
x = 8/4
x = 2
Solution to system N = (2, 2)
Diego hiked 1/3 of a mile in 2/5 of an hour. How far did he hike in one hour
Answers
Answer:
100
Step-by-step explanation:diego died
Long answer: so first we divide both fractions by 2 so that we get a more simple fraction for 2/5, which is now 1/5, and 1/3 becomes 1/6. Now since we want a full mile we multiply both the fractions by 5 so that the fraction representing time equates to 1. And 5•1/6 is 5/6.
if using the method of completing the square to solve the quadratic equation x^2 + 3x +21 =0?
Answers
Answer:
\(x= \dfrac 12 \left( -3 +i5\sqrt 3\right)\\\\x= \dfrac 12 \left( -3 -i5\sqrt 3\right)\)
Step-by-step explanation:
\(~~~~~~x^2 +3x +21 = 0\\\\\implies x^2 +3x = -21\\\\\implies x^2 + 2\cdot \dfrac 32 \cdot x + \left( \dfrac 32 \right)^2 = -21 + \left( \dfrac 32 \right)^2\\\\\implies \left(x + \dfrac 32 \right)^2 = -21+\dfrac 94\\\\\implies \left(x + \dfrac 32 \right)^2 = -\dfrac{75}4\\\\\implies x+ \dfrac 32 = \pm\sqrt{-\dfrac{75}4 \right)\\\\\implies x + \dfrac 32 = \pm i \dfrac{5\sqrt 3}{2}\\\\\implies x = -\dfrac 32 \pm i \dfrac {5\sqrt 3}2\\\\\implies x = \dfrac 12 \left( -3 \pm i5\sqrt 3\right)\)
Which of the following is equal to 6/6 - 3/6
A. 1/2
B.0
C.1
D. 1/3
Answers
Answer:
A
Step-by-step explanation:
I NEED HELP PLS HURRY
1. Write each expression with a single exponent:
a. (10^7)²
b. (10^9)³
c. (10^6)³
d. (10^2)³
e. (10³)²
f. (10^5)^7
Answers
b. 10^27
c. 10^18
d. 10^6
e. 10^6
f. 10^35
multiply the exponents.
Answer:
We use the rule,
\((a^b)^c = a^{bc}\)
a. (10^7)²
\((10^7)^2 = 10^{(7)(2)} = 10^{14}\)
10^14
b. (10^9)³
\((10^9)^3 = 10^{(9)(3)} = 10^{27}\)
10^27
c. (10^6)³
\(10^{(6)(3)}= 10^{18}\)
10^18
d. (10^2)³
\(10^{(2)(3)} = 10^{6}\)
10^6
e. (10³)²
\(10^{(3)(2)}=10^{6}\)
10^6
f. (10^5)^7
\(10^{(5)(7)} = 10^{35}\)
10^35
Step-by-step explanation:
List out the elements of the set “The letters of the word Mississippi”
Answers
Answer:
{M, i, s, p}
Step-by-step explanation:
The elements of the set are the letters in Mississippi. But remember, elements cannot repeat themselves! So the elements of this set would be {M, i, s, p} since all the other letters are just repetitions.
Hope this helps!!
The list of elements would be {M, i, s, p}
What is set?Any collection of objects (elements), which may be mathematical (e.g., numbers and functions) or not. A set is commonly represented as a list of all its members enclosed in braces. The intuitive idea of a set is probably even older than that of number.
Here the given word is Mississippi.
Now, the elements of the set are the letters present in word Mississippi.
But the elements should not repeat.
hence, the elements of this set would be {M, i, s, p}.
Learn more about set here:
https://brainly.com/question/8053622
#SPJ2
HELP! BRAINLY FOR THE FIRST ANSWER THAT'S CORRECT!!!!!!!!!

Answers
Answer:
B
Step-by-step explanation:
y = -x, all the others are just junk numbers
Answer:
The answer is B
Step-by-step explanation:
In a function, x cannot repeat. therefore, b is the answer
By the ____ we know that the measure of angle ADC is 84 degrees. a) addition property of equality b) segment addition postulatec) angle addition postulate d) substitution property of equality e) linear pair postulate
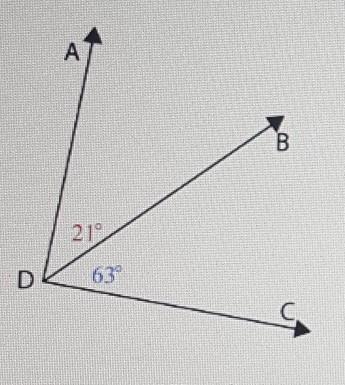
Answers
Answer;
addition property of equality
Explanation:
From the diagram shown;
From the diagram;
Substitute into the expression
ADC = 84 degrees
The postulate used was addition property of equality
Two students are throwing water balloons at a target. Accuracy is measured as how close the balloon is from the
center of the target. Tory's distances from the center of the target are approximately Normally distributed with a
mean of 123 mm and a standard deviation of 31 mm. Adam's distances from the center is approximately Normally
distributed with a mean of 108 mm and a standard deviation of 47 mm. If 5 attempts for Tory and 3 attempts for
Adam are randomly selected, what is the probability that the mean distance from the center of the target for Tory is
more than for Adam?
O 0.3113
O 0.4923
O 0.6887
O 0.7427
Answers
Answer:
0.6887
Step-by-step explanation:
Using normal distribution, the probability of that mean distance from the center of the target for Tory is more than for Adam is 0.6887.
What is normal distribution?
Normal distribution is "continuous probability distribution that its symmetrical around its mean with most values near the central peak".
According to the question,
Tory's distances from the center of the target are normally distributed with a mean of 123mm and a standard deviation 31mm. Number of attempts for Tory is 5.
Adam's distances from the center of the target are with a mean of 108mm and a standard deviation 47mm. Number of attempts for Adam is 3.
In order to find the probability of that mean distance from the center of the target for Tory is more than for Adam.
Normal distribution z = (x-μ)/σ x ~ (μ,σ)
When x = 108
z = (123 - 108)/47 [Adam's distances from the center of the target are normally distributed with a mean of 108mm and a standard deviation of Adam is 31mm.]
= 0.3191
P(x > 108) = P(z > - 0.3191)
= 1 - 0.3191 [since the probability of the normal curve is 1 and to find the area under tory mean is greater than the Adam mean only if we subtract 1 from z value]
= 0.6887
Hence, Using normal distribution, the probability of that mean distance from the center of the target for Tory is more than for Adam is 0.6887.
Learn more about Normal distribution here
https://brainly.com/question/11943392
#SPJ2
when the Dixon family traded in their old car, it had 53,790 miles on it. they had the car for 8.25 years. on average, how many miles did they drive per year?
Answers
Answer:
6,520 miles per year
Step-by-step explanation:
53,790 divided by 8.25 equals 6,520