to determine whether felonies tend to be committed more often on weekends (saturday and sunday) than on weekdays (monday through friday), a sociologist classifies a random sample of records of convicted felons in terms of these two categories. the appropriate statistical test is
Answers
It is test of two independent population means. So right should be option (a) "t for two population means (independent samples)" is correct.
Here we want to test the frequency on week days that is felonies tends to be committed more often on weekends (Saturday and Sunday) than on weekdays (Monday through Friday).
Here null hypothesis
H(0): means (Saturday and Sunday) = mean (Monday through Friday)
Alternative Hypothesis
H(1): mean (Saturday and Sunday) > mean (Monday through Friday)
So it is test of two independent population means. So right should be option (a) "t for two population means (independent samples)" is correct.
To learn more about Hypothesis link is here
brainly.com/question/29519577
#SPJ4
The right question is:
To determine whether felonies tend to be committed more often on weekends (Saturday and Sunday) than on weekdays (Monday through Friday), a sociologist classifies a random sample of records of convicted felons in terms of these two categories. The appropriate statistical test is a:
a) t for two population means (independent samples).
b) t for population correlation coefficient.
c) one-variable chi-square.
d) two-factor F
Related Questions
Determine the type of variable for:The number of counties in California.
Qualitative nominal
Quantitative Continuous
Qualitative ordinal
Quantitative discrete
Determine the type of variable for: The stages of childhood: Infant, Toddler, Preschooler, School age, Preteen, Teen
Qualitative nominal
Quantitative Continuous
Qualitative ordinal
Quantitative discrete
Suppose the average time for a class of 28 students (taken from a campus of 1200 students) to drive to campus was 23 minutes.
Select the choice
In the scenario above, 23 minutes is a parameter/ statistic , because 28 students is a sample/ population.
At a Track field, a coach keeps track of an athletes mile time. The coach reported that the mean mile time of a particular athlete was 7 minutes and the standard deviation of the mile time was 1 minute. Assume that the coach also gave us the information that the distribution of the mile time was bell shaped. Use the empirical rule to find:
What percent of the athlete's mile times are expected to be between 6 minutes and 8 minutes?
What percent of the athlete's mile times are expected to be between 4 minutes and 7 minutes?
What percent of the athlete's mile times are expected to be less than 9 minutes?
Answers
The type of variable for,
a. The number of counties in California: Quantitative discrete.
b. The stages of childhood: Qualitative ordinal.
c. In the scenario above, 23 minutes is a statistic, because 28 students is a sample.
d. Between 6 minutes and 8 minutes: Approximately 68% of the athlete's mile times are expected to be between 6 and 8 minutes, according to the empirical rule.
e. Between 4 minutes and 7 minutes: Approximately 68% of the athlete's mile times are expected to be between 4 and 10 minutes, according to the empirical rule.
f. Less than 9 minutes: Approximately 84% of the athlete's mile times are expected to be less than 9 minutes, according to the empirical rule.
In statistics, variables can be categorized into two types: qualitative and quantitative.
Qualitative variables describe characteristics or qualities that cannot be measured numerically, such as gender or hair color.
Quantitative variables, on the other hand, represent numerical values that can be measured or counted.
There are two types of quantitative variables: continuous and discrete. Continuous variables can take any numerical value within a range, such as age or weight.
Learn more about the type of a variable at
https://brainly.com/question/14501374
#SPJ4
Evaluate the expression below:
bb-a)
for b = 8, a = 4
HS Math
Answers
Answer:
60
Step-by-step explanation:
bb-a
(8)(8)-4
64-4=60
simple substitution
In 2012, the population of a city was 6.63 million. The exponential growth rate was 3.01% per year.
a) Find the exponential growth function.
b) Estimate the population of the city in 2018.
c) When will the population of the city be 11 million?
d) Find the doubling time.

Answers
Answer:
So first we need to determine what the exponential growth function would look like. Exponential growth functions look like \(P(t) = P_0*e^{r*t}\) and in our case \(P_0\) would be the initial population which is 6.63 million. R is the next variable that we need to fill out which is the rate of change which in our case is 3.01% or 0.0301.
This is how our function should look now \(P(t)=6.63*e^{0.0301*t}\)
Moving onto part b, we need to estimate the population of the city in 2018 which 6 years from 2012 and we plug that into t and solve.
\(P(t) = 6.63 * e^{0.0301*6}\)
\(P(t) = 6.63*e^{0.1806}\)
\(P(t) = 6.63 *1.1979\)
\(P(t) = 7.9423\ million\)
Moving onto part c, we need to find when the population of the city will be 11 million which will be done by setting P(t) to 11 million and solving for t.
\(11 = 6.63*e^{0.0301*t}\)
\(\frac{11}{6.63} = \frac{6.63*e^{0.0301*t}}{6.63}\)
\(1.659=e^{0.0301*t}\)
\(ln(1.659)=ln(e^{0.0301*t})\)
\(\frac{0.506}{0.0301}=\frac{0.0301*t}{0.0301}\)
\(16.818\ years = t\)
Moving onto part d, we need to find the doubling time. This will be similar to the previous part but we will be finding the time it takes to double our population. So instead of putting 11 million for P(t) we put 6.63 * 2 in there which is 13.26.
\(13.26 = 6.63*e^{0.0301*t}\)
\(\frac{13.26}{6.63} = \frac{6.63*e^{0.0301*t}}{6.63}\)
\(2=e^{0.0301*t}\)
\(ln(2)=ln(e^{0.0301*t})\)
\(\frac{0.693}{0.0301}=\frac{0.0301*t}{0.0301}\)
\(23.028\ years = t\)
Hope this helps! Let me know if you have any questions
in how many ways can three people divide among themselves six identical apples, one orange, one plum, and one tangerine
Answers
There are a total of 9 items to divide among 3 people, so the number of ways to divide the items is 84.
What is meant by the term combination?In mathematics, a combination is a selection of elements from a bigger group where the arrangement of the elements is irrelevant. Consider a collection of three letters, A, B, and C, for illustration. Two of these letters, AB, AC, and BC, can be chosen in one of three ways. "Combinations" of the letters A, B, and C are what these three options are referred to as.
C(n, k)=n!/(k!*(n-k))!
where the product of all positive integers from 1 to n, denoted by the symbol n!, is the factorial of n. For instance, 5! equals 1 + 2 + 3 + 4 + 5 = 120.
For example, three people divide among themselves six identical apples, one orange, one plum, and one tangerine.
To learn more about combination, visit:
https://brainly.com/question/19692242
#SPJ4
can someone help me solve this?

Answers
Answer:
3/5 or 1.6666666667
pls mark me brainliest
C.
Find the value of x3 + 3x²y + 3xy2 + y when x = 3 and y = 4.
涨涨涨涨
Answers
Answer:
\(x^3 + 3x\²y + 3xy^2 + y\) \(=283\)
\(When\ x = 3\ and\ y = 4\)
Step-by-step explanation:
Given
\(x^3 + 3x\²y + 3xy^2 + y\)
Required
Solve when x = 3 and y = 4
To do this, we simply substitute 3 for x and 4 for y in \(x^3 + 3x\²y + 3xy^2 + y\)
\(3^3 + 3 * 3^2 * 4 + 3 * 3 * 4^2 + 4\)
\(27 + 3 * 9 * 4 + 3 * 3 * 16 + 4\)
\(27 + 108 + 144+ 4\)
\(283\)
Hence:
\(x^3 + 3x\²y + 3xy^2 + y\) \(=283\)
\(When\ x = 3\ and\ y = 4\)
PLS HELP ASAP THANKS ILL GIVE BRAINLKEST PLS THANKS PLS

Answers
Answer:
2 vertical and -11 horizontal
Step-by-step explanation:
On a map, 3 inches represents 50 miles. Which proportion can be used to find the actual distance represented by 5 inches on the map?
Answers
Answer:
IT is B
Step-by-step explanation:
edge duh
A bank manager wants to encourage new customers to open accounts with principals of at least $. He decides to make a poster advertising a simple interest rate of %. What must the principal be if the bank manager also wants to advertise that one can earn $ the first month? Can the poster correctly say, "Open an account of $ and earn at least $ interest in 1 month!"?
Answers
Hope this helps!!
Please answer this question with a decent explanation ty.

Answers
Check the picture below.
\(\textit{Law of Cosines}\\\\ \cfrac{a^2+b^2-c^2}{2ab}=\cos(C)\implies \cos^{-1}\left(\cfrac{a^2+b^2-c^2}{2ab}\right)=\measuredangle C \\\\[-0.35em] ~\dotfill\\\\ \cos^{-1}\left(\cfrac{21^2+32^2-26^2}{2(21)(32)}\right)=\measuredangle J \implies \cos^{-1}\left(\cfrac{ 789 }{ 1344}\right)=\measuredangle J\implies \boxed{54.1^o\approx \measuredangle J}\)
Make sure your calculator is in Degree mode.

For What Values Of X And Y Are The Triangles To The Fight Congruent By HL? X = And Y =
Answers
The values of x and y the triangles to the fight congruent are x = 3 and
y = 1.
What is congruent triangles?
Triangles with the same size and shape are said to be congruent. This implies that the corresponding sides and angles are both equal. Without comparing every angle and side of the two triangles, we can determine whether two triangles are congruent.
If given these triangles are congruent then all corresponding side must be equal
As we can see that both triangle are right triangle
Therefore hypotenuse of one triangle equal to another
x+1 = 4y ..... (A)
And lenght ( height) of one must equal to another triangle
x = y +2 .... (B)
therefore
Plug the value of x = y + 2 in equation A
y + 2 + 1 = 4y
3y = 3
y = 1
and x = y+2
x = 1 + 2
x = 3
Hence, the values of x and y the triangles to the fight congruent are
x = 3 and y = 1.
To know more about congruent triangles, click on the link
https://brainly.com/question/2938476
#SPJ4
Complete question:
Complete question is attached below.

There are`50` sq. mm of bacteria in a Petri dish.
The bacteria grow exponentially and `1` hour later, there are `70` sq. mm of bacteria in a Petri dish.
What is the growth factor that models the hourly growth of this bacteria?
Answers
The required growth factor that models the hourly growth of this bacteria is 2/5
What is Exponential increment?Some things develop at a predictable rate. As the overall number increases, certain things, like money or the offspring of mated rabbits, can expand exponentially faster. Growth is exponential when it accelerates in proportion to the expanding total population.
According to question:We have,
50 sq mm of bacteria and they are increased to 70 sq mm in 1 hour.
Then,
To find the factor Divide the increased value by initial value.
So
increased value = 70 - 50 = 20 sq mm
And initial value = 50
Then,
= 20 / 50
= 2/5
Thus, required growth factor is 2/5.
To know more about Factor visit:
brainly.com/question/28983916
#SPJ1
5. CATERED DINNER The Striton family had a meal catered for a wedding rehearsal dinner. The cost of the dinner was $476. There was a 5% sales tax and they left a 15% tip. What was the total cost including the sales tax and the tip?
Answers
Answer: $571.20
Step-by-step explanation:
In this question, you're gonna use multiplication to figure out the tax and the tip.
If the dinner is $476 and the tax is 5%, multiply the two to figure out how much the sales tax is.
476 • 0.05 = 23.80
Then, multiply the $476 and 15% to figure out the tip.
476 • .15 = 71.40
Add them all up.
476 + 71.40 + 23.80 = 571.20
In this case, the Striton family paid $571.20 altogether.
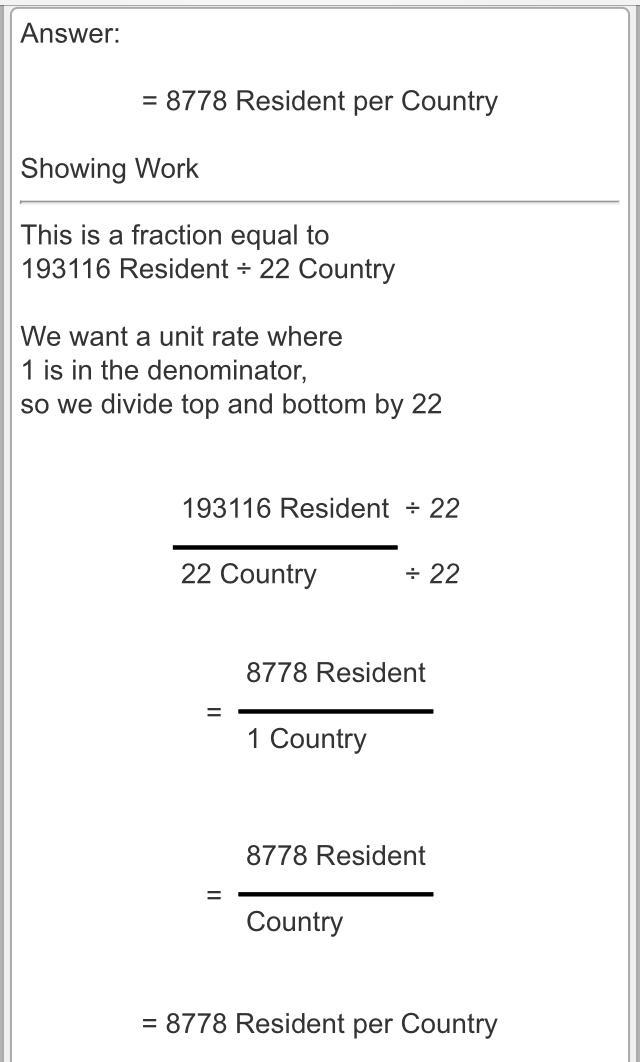
A cookie recipe requires 2 cups of chocolate chips to make 32 cookies if 100 cookies are to be baked how many cups of chocolate chips will be needed
Answers
Answer:
she would need 6.25 cups of chocolate chips
Step-by-step explanation:
32/2= 16
each cup can make 16 cookies
100/16=6.25
this should be right, have a good day
Help? please!!!
Result of problem 2 5/6 - 4/5 + 1.75 = .....?
Anyone want to answer???
Answers
Answer: 227/ 60 = 3 47/60 OR 3.783
Note: If you don't get the right answer because of the extra 3 in 3.783 then simply remove the extra 3 at the end.
Explanation:
Step 1: Multiply the whole number 2 by the denominator 6. Whole number 2 equally.
Step 2: Add the answer from the previous step 12 to the numerator 5. New numerator is 12 + 5 = 17
Step 3: Write a previous answer (new numerator 17) over the denominator 6
Message: If you found this helpful let me know by giving a thanks! :)
is 0.032 a terminating decimal
Answers
Haruka hiked several kilometers in the morning. She hiked only
6
66 kilometers in the afternoon, which was
25
%
25%25, percent less than she had hiked in the morning.
How many kilometers did Haruka hike in all?
Answers
Answer:
14 km
Step-by-step explanation:
6 = M - .25M = .75M
M = 6/.75 = 8 km in the morning
8 + 6 = 14
encuentra el MCM de 12 y 24
Answers
【Rep.】The least common multiple of 12 and 24 is 24.
\(\red{ {\hspace{50 pt}\above 1.2pt}\boldsymbol{\mathsf{Procedure}}{\hspace{50pt}\above 1.2pt}}\)
To obtain the least common multiple (lcm) we must do it by simultaneous decomposition.
This method consists of extracting the common and uncommon prime factors, then
\(\large\displaystyle\text{$\begin{gathered}\sf \left.\begin{matrix} \blue{12 \ \ \ 24}\\ \ 6 \ \ \ 12\\ \ 3 \ \ \ \ 6\\ \ 3 \ \ \ \ 3\\ \ 1 \ \ \ \ 1 \end{matrix}\right|\begin{matrix} 2\\ 2\\ 2\\ 3\\ \: \end{matrix} \end{gathered}$}\)
\(\sf{L.c.m.(12,24)=2\times2\times2\times3}\)
\(\sf{L.c.m.(12,24)=2^{3}\times3 }\)
\(\boxed{\boxed{\sf{L.c.m.(12,24)=24}}}\)
{ Pisces04 }Sketch graphs of the following quadratic
y = (x + 2)² - 1
Answers
The graph of the quadratic equation is in the form of parabola.
In mathematics, a parabola is a roughly U-shaped, mirror-symmetrical planar curve. The same curves can be defined by a number of seemingly unrelated mathematical definitions, which all correspond to it.
A line and a point (the focus) are two components of one definition of a parabola (the directrix). There is less emphasis on the directrix. The parabola is the subset of sites in that plane that are equally spaced apart from both the directrix and the focus.
A parabola, also referred to as a continuous line, is formed when a right ring conical surface and a plane transverse to another plane that is also tangential to the conical surface cross.
The parabola has the equation y = (x + 2)² - 1
Using the general form of the parabola we can define the vertex of the parabola at (-2,-1) .
The graph of the parabola is attached below.
The graph passes the x axis at (-1,0) and (-3,0) and (0,3) .
To learn more about quadratic visit:
https://brainly.com/question/22364785
#SPJ9

determine the rejection region. select the correct choice below and fill in the answer box(es) within your choice. (round to three decimal places as needed.) a. t>enter your response here your answer is not correct.b. tenter your response here part 3 determine the proper conclusion. ▼ h0. there is ▼ evidence to indicate μ is ▼ 3.
Answers
The rejection region for a hypothesis test can be found, we need to specify the significance level (α) and the test statistic distribution.
Given that the question mentions "t" and asks us to round to three decimal places, we can infer that we are dealing with a t-test and should use the t-distribution.
The rejection region for a t-test is located in the tails of the t-distribution. The specific critical values depend on the degrees of freedom and the significance level (α).
Since the question does not provide the degrees of freedom or the significance level, we cannot provide a specific answer. However, I can explain the general procedure:
1. Determine the degrees of freedom based on the sample size and test conditions.
2. Determine the critical value(s) for the desired significance level (α) from the t-distribution table or a statistical software.
3. If the calculated test statistic (t) falls within the rejection region (tails of the t-distribution), we reject the null hypothesis (H0). Otherwise, we fail to reject the null hypothesis.
To know more about the Hypothesis Test visit:
https://brainly.com/question/29727211
#SPJ11
Someone who wants to go camping in the spring starts to pack his backpack and this camper must pack three items: food, first-aid kits, and clothes. The backpack has a capacity of 9 ft 3. Each unit of food takes 2ft 3 . A first-aid kit occupies 1ft 3 , and each piece of cloth takes about 3ftt 3 . The hiker assigns the benefit of the items as 7, 5 , and 6 to food, first aid, and clothes, respectively, which means that foods are the most valuable of the three items. From experience, the hiker must take at least one unit of each item. How many of each item should the camper take?
Answers
The camper should take 3 units of food, 1 first-aid kit, and 1 piece of clothing within the given constraints.
To determine the optimal number of each item the camper should take, we need to maximize the total benefit while considering the capacity constraint of the backpack.
Let's assume the camper takes x units of food, y first-aid kits, and z pieces of clothing.
The backpack has a capacity of 9 ft^3, and each unit of food takes up 2 ft^3. Therefore, the constraint for food is 2x ≤ 9, which simplifies to x ≤ 4.5. Since x must be a whole number and the camper needs at least one unit of food, the camper can take a maximum of 3 units of food.
Similarly, for first-aid kits, since each kit occupies 1 ft^3 and the camper must take at least one, the constraint is y ≥ 1.
For clothing, each piece takes 3 ft^3, and the constraint is z ≤ (9 - 2x - y)/3.
Now, we need to maximize the total benefit. The benefit of food is assigned as 7, first aid as 5, and clothing as 6. The objective function is 7x + 5y + 6z.
Considering all the constraints, the possible combinations are:
- (x, y, z) = (3, 1, 0) with a total benefit of 7(3) + 5(1) + 6(0) = 26.
- (x, y, z) = (3, 1, 1) with a total benefit of 7(3) + 5(1) + 6(1) = 32.
- (x, y, z) = (4, 1, 0) with a total benefit of 7(4) + 5(1) + 6(0) = 39.
- (x, y, z) = (4, 1, 1) with a total benefit of 7(4) + 5(1) + 6(1) = 45.
Among these combinations, the highest total benefit is achieved when the camper takes 3 units of food, 1 first-aid kit, and 1 piece of clothing.
Therefore, the camper should take 3 units of food, 1 first-aid kit, and 1 piece of clothing to maximize the total benefit within the given constraints.
Learn more about objective function here:
brainly.com/question/33272856
#SPJ11
Can someone help me quick. I really need help!! I’ll mark brainliest!! Please & thank youuu!

Answers
~Kindly see the attached picture!
✧ Hope I helped ! ✧
Have a wonderful day / night ! ♡
Let me know if you have any questions regarding my answer ツ
\( \underline{ \underline{ \mathfrak{Carry \: on \: learning}}}\) !! ✎
▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁

Help
Will
Give
Brainlist
Answers
Answer:
1st answer
Step-by-step explanation:
3x^4 + 9x^3 - 5x^2 - 14x - 7 divided by x + 3 using synthetic division
Answers
Answer:
\(3x^3 - 5x + 1 - \frac{10}{x + 3}\)
or
3x^3 - 5x + 1
Remainder: -10
Step-by-step explanation:
Please see attached image for full explanation!
1.) Write the coefficient of each term.
2.) Beginning with 3, multiply by -3, or x + 3 = 0 (the divisor.)
3.) Add the product to the next coefficient and repeat until you get to the last number, -7.
4.) You should have the numbers 3, 0, -5, 1, and -10.
5.) Rewrite this quotient as an equation:
3x^3 - 5x + 1
Note that the highest power is 3, one less than that of the highest power in the original equation.
6.) Don't forget the remainder!
You can include this in the equation or not, depending on the instructions.
Therefore, the final answer is 3x^3 - 5x + 1 - 10/x+3 or 3x^3 - 5x + 1 R: -10.

During a musical an orchestra is playing. As the music plays, the volume changes in the beginning of the piece can be modeled by the equation s = 10│x - 4│+ 50 where s represents the sound level in decibels and x represents the number of measures of music played. Explain in words each step to find the following question:
At what number(s) measures played would the sound level be at 80 decibels?
Answers
Answer:
The numbers of measure of music played are 1 and 7
Step-by-step explanation:
Given
\(s = 10|x - 4| + 50\)
Required
Solve for x when s = 80
Substitute 80 for x
\(80 = 10|x - 4| + 50\)
Subtract 50 from both sides
\(80 - 50= 10|x - 4| + 50 - 50\)
\(30= 10|x - 4|\)
Divide through by 10
\(\frac{30}{10}= \frac{10|x - 4| }{10}\)
\(3= |x - 4|\)
Reorder
\(|x - 4| = 3\)
This can be split into
\(x - 4 = 3\) or \(x - 4 = -3\)
Solve for x
\(x = 4 + 3\) or \(x = 4 - 3\)
\(x = 7\) or \(x = 1\)
Hence:
The numbers of measure of music played are 1 and 7
I WILL GIVE BRAINLIEST plz hurry Let f(x) = |2|+5
The graph of f(x) is transformed into the graph of g(x) by a translation of 3 units left
and a translation of 6 units up. What is the equation for g(x)? (4 points)
Answers
Answer: f(|x|+3)=||x|+3|
Step-by-step explanation:
Find the exact value of the expression. Given cosθ=135 and sinθ<0; find cscθ.
Answers
The exact value of cscθ is (35 * √(1190)) / 1190.
To find the value of cscθ (cosecant θ) given that cosθ = 1/√35 and sinθ < 0, we can use the reciprocal relationship between sine and cosecant.
Recall that cscθ is the reciprocal of sinθ. Since sinθ is negative, we can determine its value based on the quadrant in which θ lies.
In the unit circle, the cosine is positive in the first and fourth quadrants, while the sine is negative in the third and fourth quadrants.
Given that cosθ = 1/√35 and sinθ < 0, we can conclude that θ lies in the fourth quadrant.
Using the Pythagorean identity, sinθ = √(1 - cos^2θ), we can calculate the value of sinθ:
sinθ = √(1 - (1/√35)^2)
= √(1 - 1/35)
= √(34/35)
= √34 / √35
= (√34 / √35) * (√35 / √35) [Multiplying numerator and denominator by √35 to rationalize the denominator]
= √(34 * 35) / 35
= √(1190) / 35
Now, since cscθ is the reciprocal of sinθ, we have:
cscθ = 1 / sinθ
= 1 / (√(1190) / 35)
= 35 / √(1190)
= (35 * √(1190)) / 1190.
Learn more about Pythagorean identity here:
https://brainly.com/question/24220091
#SPJ11
A salesperson purchased a car that is advertised as getting 3 times as many miles per gallon of gasoline on the highway than it does in the city. On a recent sales trip that covered 1500 miles in total, the car used up 18 gallons on the highway and 7 gallons in the city. Assuming that the advertised mileage estimates were correct, how many miles per gallon of gasoline does the car get in the city and on the highway
Answers
The car gets 214.3 miles per gallon of gasoline in the city and 27.8 miles per gallon of gasoline on the highway.
Let the number of miles per gallon that the car gets in the city be x. Hence, the number of miles per gallon that the car gets on the highway would be 3x.
A salesperson purchased a car that is advertised as getting 3 times as many miles per gallon of gasoline on the highway than it does in the city. On a recent sales trip that covered 1500 miles in total, the car used up 18 gallons on the highway and 7 gallons in the city.
Calculation of miles per gallon of gasoline in the city:7 gallons of gasoline cover city distance: x miles is covered by 1 gallon of gasoline.
Thus, 7 gallons will cover 7x miles. Hence, we can equate: 7x = 1500 ....(1)
Calculation of miles per gallon of gasoline on the highway:18 gallons of gasoline cover the highway distance.3x miles is covered by 1 gallon of gasoline.
Thus, 18 gallons will cover 54x miles.
Hence, we can equate: 54x = 1500 ....(2)
Dividing equation (1) by 7:7x/7 = 1500/7x
= 214.3 miles per gallon of gasoline in the city.
Dividing equation (2) by 54:54x/54
= 1500/54x
= 27.8 miles per gallon of gasoline on the highway.
Therefore, the car gets 214.3 miles per gallon of gasoline in the city and 27.8 miles per gallon of gasoline on the highway.
To learn more about gasoline visit;
https://brainly.com/question/14588017
#SPJ11
f(n) = n² – 3 g(n) = 4n - 1 Find f[g(1)]
Answers
Answer:
f[g(1)]=6.
Explanation:
Given f(n) and g(n) defined below:
\(\begin{gathered} f\mleft(n\mright)=n^2-3 \\ g\mleft(n\mright)=4n-1 \end{gathered}\)First, we evaluate g(1):
\(\begin{gathered} g\mleft(1\mright)=4(1)-1 \\ =4-1 \\ g(1)=3 \end{gathered}\)Therefore:
\(\begin{gathered} f\mleft(g(1)\mright)=f\mleft(3\mright) \\ f\mleft(3\mright)=3^2-3 \\ =9-3 \\ =6 \end{gathered}\)Therefore, f[g(1)]=6.
Use f(x) log6(36x) and g(x) = 6* to answer the questions below. (a) Find f(g(x)) and simplify. 36+ x 36x 6 + x 2+ x 2x (b) Find the range of y f(x) +g(x) (-0, ) [6, 00) (0, o) O[1, 0o) O (1/36, o)
Answers
To find f(g(x)), substitute g(x) into f(x). Simplifying gives f(g(x)) = log6(36g(x)). For range of y in f(x) + g(x), Take possible values . Since log6(36x) is defined for x > 0, and 6 is positive, the range of y is (0, ∞).
a) To find f(g(x)), we substitute g(x) into f(x):
f(g(x)) = f(6x) = log6(36(6x)) = log6(216x) = log6(6^3x) = 3log6(6x) = 3(log6(6) + log6(x)) = 3(1 + log6(x)) = 3 + 3log6(x).
Thus, f(g(x)) simplifies to 3 + 3log6(x).
(b) To find the range of y in f(x) + g(x), we need to consider the possible values of f(x) and g(x). Since log6(36x) is defined for x > 0, and 6* is always positive, the range of f(x) is (0, ∞). Similarly, g(x) = 6* is always positive, so the range of g(x) is also (0, ∞).When we add f(x) and g(x), we are adding two positive functions, resulting in values greater than 0. Therefore, the range of y in f(x) + g(x) is (0, ∞).
To learn more about range click here : brainly.com/question/29204101
#SPJ11