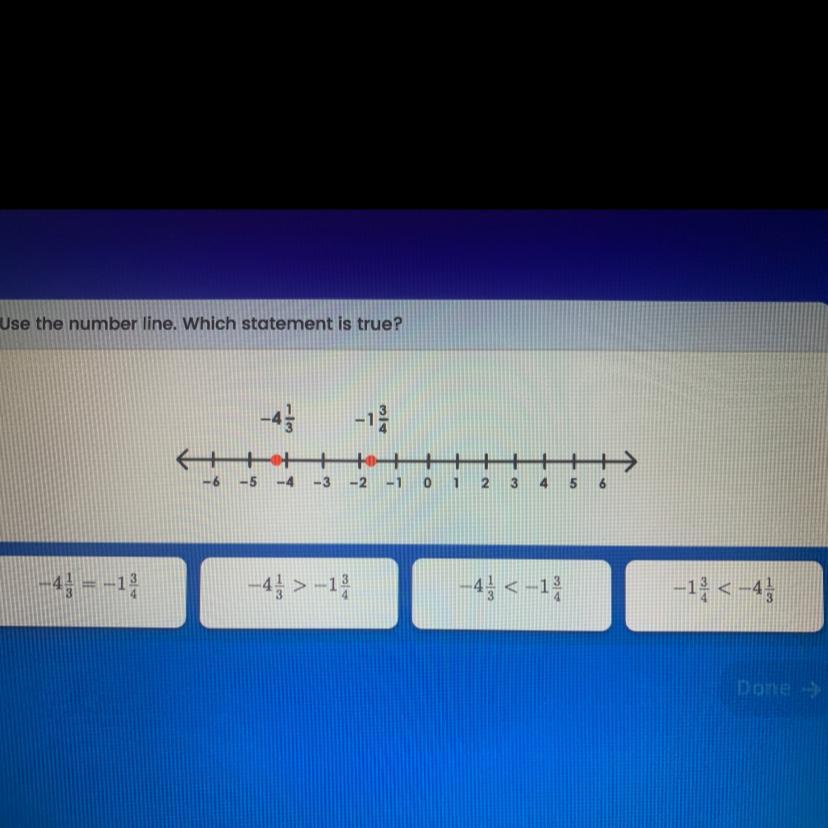
Answers
Related Questions
(a) Can a triangle have two obtuse angles? (b) Can a triangle have two right angles? (c) Suppose no angle of a triangle measures more than 60°. What do you know about the triangle?
Answers
(a) No, a triangle cannot have two obtuse angles. (b) No, a triangle cannot have two right angles.
(c) If no angle of a triangle measures more than 60°, then the triangle is an acute triangle.
(a) In a triangle, the sum of all three angles must be 180°. Since two obtuse angles would sum to more than 180°, it is not possible for a triangle to have two obtuse angles.
(b) In a triangle, the sum of all three angles must be 180°. Since two right angles would sum to 180°, it is not possible for a triangle to have two right angles.
(c) In an acute triangle, all three angles are less than 90°. If no angle of a triangle measures more than 60°, then all three angles are less than 90°, making it an acute triangle.
To know more about Angles visit.
https://brainly.com/question/13954458
#SPJ11
Which distribution will have a positive skew?
{1, 2, 3, 4, 5, 5, 5, 6, 6, 7, 8}
{1, 2, 3, 4, 5, 6, 7, 8}
{1, 2, 2, 3, 3, 3, 4, 4, 5, 6, 7, 8}
{1, 2, 3, 4, 4, 5, 5, 5, 6, 6, 7, 8, 9}
Answers
Answer:
the second one
Step-by-step explanation:
and go to Mr.beast.com
if a square has the same perimeter as this rectangle, what is the length of one side?
Answers
The length of one side of a square will be \((\frac{l+b}{2} )\) where, "l" is the length of the rectangle and "b" is the breadth, if a square has the same perimeter as this rectangle.
As per the question statement, the perimeter of square is equal to that of a rectangle.
From this above mentioned condition, we will have to calculate the length of one side of the square.
Since no numerical data is provided about the "l' and "b" of the rectangle in the question statement, we will go ahead with "l' and "b" as variables to calculate a generalized answer.
We know that, the formula to calculate the perimeter of a rectangle goes as
\([2*(l+b)]\) where, "l" is the length of the rectangle and "b" is the breadth.
As per the question-mentioned condition, the perimeter of our generalized square is also \([2*(l+b)]\)
But the formula to calculate the perimeter of a square goes as (4*a), where "a" is the length of one side of the square.
Therefore, \(4a = 2(l+b)\\\)
\(or, a=\frac{2(l+b)}{4}\\ or, a=\frac{(l+b)}{2}\)
Square: In Euclidean plane geometry, a square is a quadrilateral with four right angles and 4 equal sides, i.e., more specifically can be defined as a parallelogram with all four interior angles being right-angles and all four sides being equal.Perimeter: In Euclidean plane geometry, perimeter is the continuous line forming the boundary of a closed geometrical figure.To learn more about Perimeters and Squares, click on the link below.
https://brainly.com/question/11495285
#SPJ9
help with my geometry please

Answers
Answer:
x = 11
z = 86
Step-by-step explanation:
8x + 6 and 10x-16 are vertical angles
Vertical angles are pairs of angles that are opposite each other and have the same vertex, or point of intersection. They are formed when two lines intersect at a point, and are always congruent, or of equal measure.
To solve this equation, we need to isolate the variable x on one side of the equation. To do this, we can start by subtracting 6 from both sides of the equation:
8x + 6 - 6 = 10x - 16 - 6
8x = 10x - 22
Now we can subtract 8x from both sides of the equation:
8x - 8x = 10x - 22 - 8x
0 = 2x - 22
To solve for x, we can add 22 to both sides of the equation:
0 + 22 = 2x - 22 + 22
22 = 2x
Finally, we can divide both sides of the equation by 2 to find the value of x: 22 / 2 = 2x / 2
x = 11
Therefore, the solution to the equation is x = 11.
Now that we have x, z is a supplementary angle to 8x + 6 (or you could do 10x - 16)
Supplementary angles are pairs of angles that add up to 180 degrees. They are formed when two lines intersect at a point, and the angles formed at the intersection are supplementary.
First plug in x, 8x + 6 = 8(11) + 6 = 88 + 6 = 94
180 - 94 = z
z = 86
16. A map is drawn on a coordinate plane.
Each unit represents 10 miles. Terri
drives from her home at point G to her
friend's home at point H, following the
route shown below. Terri drives steadily
at 50 miles per hour. How long is the
distance between the two points? How
long will it take Terri to get from point
G to point H?
Answers
Answer:
can't answer without the picture because you need the route to know how far.
Help me please I'm confused

Answers
Answer:
The point (x, y) = (3, -4) represents the solution of the given system of equations.
Please check the attached graph.
Step-by-step explanation:
Given the system of equations
\(y\:=\:-\frac{3}{2}x\:-\:3\)
\(y\:=\:-x\:-\:1\)
Please check the attached graph of the given system of equations
From the graph:
The red line represents the equation: \(y\:=\:-\frac{3}{2}x\:-\:3\)The blue line represents the equation: \(y\:=\:-x\:-\:1\)Point of Intersection:
We know that the point of intersection of two lines represents the solution of the system of equations.It is clear from the attached graph that the two lines intersect at the point (-4, 3).
i.e. at x = -4, y = 3
Therefore, the point (x, y) = (3, -4) represents the solution of the given system of equations.
Please check the attached graph.

Please help me! I have discalculia and can't figure this out for the life of me


Answers
The answer is that Point D is Circumcentre and other lengths DE,DF,DG are perpendicular bisectors of sides of triangle ABC
What is Circumcentre?
The point of intersection of Perpendicular bisectors in a triangle is called called Circumcentre.
Solution;
The circumcentre is equidistant from all sides of an triangle when we draw the perpendicular from this point to sides of triangles, the length of all perpendiculars will be same and this is its another property
To learn more about circumcentre click the below link:
https://brainly.com/question/14368399
#SPJ1
Please help I’m struggling

Answers
Answer:
I believe the answer is 23.
Step-by-step explanation:
90-67=23
Consider the function f(x)= 10% and the function g(x), which is shown below. How will the graph of g(x) differ from the graph of f(x)?
g(x) = f(z - 6)
<=10(-6)
O A.
The graph of g(x) is the graph of f(x) shifted 6 units up.
OB.
The graph of g(x) is the graph of f(x) shifted to the left 6 units.
OC. The graph of g(x) is the graph of f(x) shifted 6 units down.
OD. The graph of g(x) is the graph of f(x) shifted to the right 6 units.
s reserved.

Answers
Step-by-step explanation:
SUBTRACTING '6' from the 'x' of the equation shifts the graph '6' units to the RIGHT .
Ix runners are doing the 100 meter dash. the winner receives a blue ribbon and the second place runner gets a red ribbon. how many ways can the ribbons be awarded?
Answers
The number of ways the ribbons can be awarded in a race with "x" runners is x * (x-1).
The number of ways the ribbons can be awarded depends on the total number of runners participating in the 100-meter dash.
If there are "x" runners participating, the winner can be any one of the x runners, and the second-place runner can be any one of the remaining (x-1) runners.
Therefore, the number of ways the ribbons can be awarded is equal to the number of possible choices for the winner multiplied by the number of possible choices for the second-place runner.
Mathematically, this can be expressed as:
Number of Ways = x * (x-1)
For example, if there are 5 runners in the race, there are 5 ways to choose the winner. After selecting the winner, there are 4 remaining runners from which we can choose the second-place runner. So, in this case, the number of ways the ribbons can be awarded is:
Number of Ways = 5 * 4 = 20
In general, the number of ways the ribbons can be awarded in a race with "x" runners is x * (x-1).
Learn more about ribbons here
https://brainly.com/question/7982465
#SPJ11
Solve for x Log2 x=-5
Answers
Determine if there is a correlation and slope for the
scatterplot
positive correlation, positive slope
positive correlation, negative slope
negative correlation, negative slope
* no correlation, undefined slop

Answers
Answer:
A
Step-by-step explanation:
Answer:
its D
Step-by-step explanation:
edge 2021
7. What is the volume of a cylinder with a radius of 5and a height of 3?A. 30mB. 45mC. 75mD. 120m
Answers
Given
\(\begin{gathered} r=5 \\ h=3 \end{gathered}\)The formula of the volume of a cylinder
\(Volume\text{ of a cylinder=}\pi r^2h\)Substitute the given to the volume
\(\begin{gathered} Volume=\pi\times5^2\times3 \\ Volume\text{ =75}\pi \\ Volume=\text{ 235.62 unit}^3 \end{gathered}\)The volume of a cylinder with a radius of 5 and a height of 3 is
\(235.62\text{ unit}^3\)pls someone help quick

Answers
Answer: Aleah i think the answer is g
Step-by-step explanation:
Find the value.
X3-4 when x=3
PLEASE HELP!!! ASAP!!!
Answers
Answer:
23
Step-by-step explanation:
Raise 3 to the power of 3
27 - 4
Subtract 4 from 27
23
Hope this was correct
Answer:
23
Explanation:
step 1 - rewrite the expression with the value of x
\(x^3 - 4\)
\((3)^3 - 4\)
step 2 - solve the exponent
\((3)^3 - 4\)
\(27 - 4\)
step 3 - subtract
\(27 - 4\)
\(23\)
therefore, the value of the expression is 23.
ane must select 3 different items for each dinner she will serve. the items are to be chosen from among 5 different vegetarian and 4 different meat selections. if at least one of the selections must be vegetarian, how many different dinners can jane create?
Answers
The total number of different dinners created by Jane from the given number of selections is equal to 140.
The number of different dinners Jane can create,
Consider two cases,
One vegetarian selection and two meat selections
Here,
We have 5 choices for the vegetarian selection, and 4 choices for each of the meat selections,
Total possible dinners are
= 5 × 4 × 4
= 80 .
Two vegetarian selections and one meat selection
Here,
We have 5 choices for the first vegetarian selection,
4 choices for the second vegetarian selection,
And 4 choices for the meat selection.
Total possible dinners are,
= 5 × 4 × 4
= 80 .
However, we have counted some dinners twice,
The ones that have two vegetarian selections and one meat selection.
There are 5 × 4 = 20 such dinners, subtract this number from the total.
Total number of different dinners Jane can create, given that at least one of the selections must be vegetarian is,
80 + 80 - 20 = 140
Therefore, the number of different dinners created by Jane is equal to 140 .
Learn more about dinners here
brainly.com/question/31076710
#SPJ4
The above question is incomplete, the complete question is:
Jane must select 3 different items for each dinner she will serve. the items are to be chosen from among 5 different vegetarian and 4 different meat selections. if at least one of the selections must be vegetarian, how many different dinners can jane create?
Whats the variable for 4/2 = 3/x
Answers
Answer: 3/2
Step-by-step explanation:
We can cross multiply.
4x = 6.
Divide both sides by 4.
x = 6/4 which simplifies to 3/2
Determine weather the triangles a are similar

Answers
Answer:
Step-by-step explanation:

Write equation in slope intercept form (x=mx+b). Find the slope (x) and the y-intercept (b) of the line

Answers
Answer:
y = 4x - 3
Step-by-step explanation:
When x = 0, y = -3
When y = 0, x = 3/4
it is instructive to see how picard’s method works with a choice of the initial approximation other than the constant function y0(x) = y0. apply the method to the initial value problem (4) with (a) y0(x) =ex (b) y0(x) =1+x (c) y0(x) = cos x
Answers
The initial value problem of equivalent integral equation is:
y(x) = \(e^x\) is y(x) = x²y(x) = 1+x is y(x) = 1+x+2[\(e^x-x-1\)]y(x) = cosx is given by y = -sinx - x + \(\frac{x^3}{3!}\) + 1 +x + x² + x³/3! + x⁴/3!1) Given initial value problem is:
\(\frac{dy}{dx} =x+y\)
y(x) = \(e^x\) , y = 1
The equivalent integral equation is,
\(y = y_o + \int\limits^x_0 {(s+e^s)} \, dx \\\)
Then by pieard's method,
\(y = 1 + \int\limits^x_0 {(s+e^s)} \, dx \\= 1+\int\limits^0_xsds+\int\limits^x_0 {e^s} \, dx\)
\(= 1+\frac{x^2}{2} +e^x\)
y(x) = \(e^{x^2}\) -1
y(x) = x²
2) The given initial value problem is,
\(\frac{dy}{dx} =x+y\)
y(x) = 1+x
The equivalent integral equation is,
\(y = y_o + \int\limits^x_0 {(s+e^s)} \, dx \\\)
Then by pieard's method,
\(y = 1 + \int\limits^x_0 {(s+1+s)} \, dx \\\\= 1+\int\limits^0_x {(1+2s)} \, dx \\= 1+[s]^x_0+2[\frac{s^2}{2} ]^x_0\\=1+x+x^2\)
y(x) = 1+x+2[\(e^x-x-1\)]
3) The given initial value problem is,
\(\frac{dy}{dx} =cosx\)
y(x) = cosx
The equivalent integral equation is,
\(y = y_o + \int\limits^x_0 {(s+e^s)} \, dx \\\)
Then by pieard's method,
\(y = 1 + \int\limits^x_0 {(s+cos s)} \, dx \\\\= 1+\frac{x^2}{2}+sinx \\ = (sinx-x)+1+x+\frac{x^2}{2}\)
y = -sinx - x + \(\frac{x^3}{3!}\) + 1 +x + x² + x³/3! + x⁴/3!
Leran more
A piece of fabric 20m long sew 4/5 of that cloth, the rest of the fabric is sewn for each bag 2/3m, how many bags can be sewn in all?
Answers
Answer: 16 bags
Step-by-step explanation:
(20) (4/5) = 16
(16) (3) / 2 = 24
point is 9 units from the center of a circle of radius 15. how many different chords of the circle contain and have integer lengths?
Answers
Total number of different chords of the circle passing through point P with integer lengths is equal to 7.
As given in the question,
Radius of the circle = 15units
Longest chord of the circle 'diameter' = 2 × 15
= 30units
Point 'P' is 9 units away from the circle.
Consider shortest distance( perpendicular) of point P for shortest chord.
Half length of the chord , shortest distance and radius form right triangle.
(1/2) length of the chord = √15² - 9²
= √225 - 81
= 12units
Length of the chord = 2(12)
= 24 units
Different Chords with integer length = 24, 25, 26, 27, 28 , 29 , 30
Total number of different chords = 7
total number of chords = 6 original + 6 mirror image + 1 longest chord
= 13
Therefore, total chords with different integer length passing through the point P of the circle is 7.
The complete question is :
A point P is at the 9 unit distance from the center of a circle of radius 15 unit. How many total number of different chord of the circle passing through the point P and have the integer lengths?
Learn more about chords here
brainly.com/question/21686011
#SPJ4
The following data follows the functional form y-ax sin(2Tx) X 0.25 0.75 1.25 1.75 2.25 2.75
Y 3.09 -1.21 0.84 -0.69 0.49 -0.44 (a) Determine a and b by the method of least squares Determine (b) the standard deviations of a 'and b' namely, the corresponding constants of the linearized fit. (c) Plot the fit on log-log paper along with the data.
Answers
Determining (a) a and b by the method of least squares: a = 1.084 and b = 3.061. (b) The standard deviations of a and b: σ_a = 0.107 and σ_b = 0.090. (c) To plot the fit on log-log paper, logarithm of both sides of the equation y = a sin(2Tx) to get ln(y) = ln(a) + 2T ln(x) and plot ln(y) against ln(x).
(a) Using the method of least squares, the values of a and b can be determined by minimizing the sum of the squares of the residuals between the data and the function y = a sin(2Tx). Solving for a and b, we get a = 1.084 and b = 3.061.
(b) The standard deviations of a and b can be calculated using the following equations:
σ_a = √(Σ(residuals²)/(n-2)) * √(1/(nΣ(x²)-Σ(x)²))
σ_b = √(Σ(residuals²)/(n-2)) * √(n/(nΣ(x²)-Σ(x)²))
Using the given data and the values of a and b from part (a), we get σ_a = 0.107 and σ_b = 0.090.
(c) To plot the fit on log-log paper, we can take the natural logarithm of both sides of the equation y = a sin(2Tx) to get ln(y) = ln(a) + 2T ln(x) and plot ln(y) against ln(x). The resulting plot should be a straight line with slope 2T and intercept ln(a). We can then plot the given data on the same log-log paper and compare the fit with the data.
To know more about logarithm, refer here:
https://brainly.com/question/30226560#
#SPJ11
Complete question:
The following data follows the functional form y-ax sin(2Tx)
X 0.25 0.75 1.25 1.75 2.25 2.75
Y 3.09 -1.21 0.84 -0.69 0.49 -0.44
(a) Determine a and b by the method of least squares
(b)Determine the standard deviations of a 'and b' namely, the corresponding constants of the linearized fit.
(c) Plot the fit on log-log paper along with the data.
Is 25 a prime number?
Answers
No, 25 is not a prime number. It can be divided by 5 without a remainder, so it has factors other than 1 and itself.
A prime number is a positive integer greater than 1 that has no positive integer divisors other than 1 and itself. In other words, a prime number can only be divided evenly by 1 and by itself. They are considered to be the "building blocks" of the natural numbers, and are important in number theory and other branches of mathematics.
The factors of 25 are 1, 5 and 25. Prime numbers are numbers that are divisible by only 1 and themselves. So 25 is not a prime number.
To know more on prime number
https://brainly.com/question/11799672
#SPJ4
HELP PLZ. Which of the following statements about the graph is true.
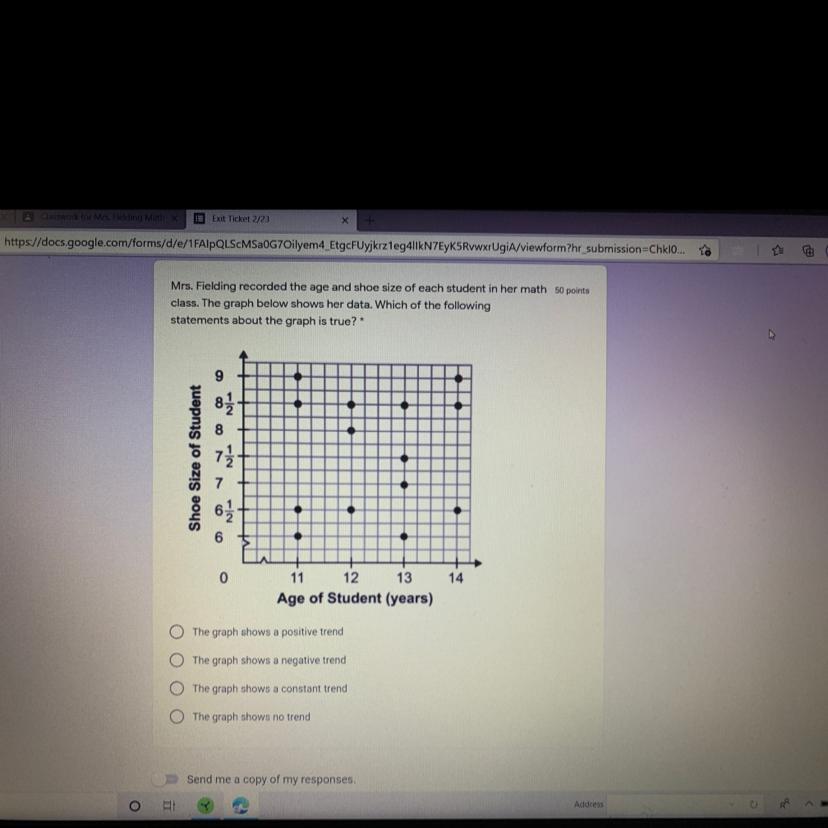
Answers
Answer:
D: The graph shows no trend.
Step-by-step explanation:
The points on the graph are very random. It can't be A or B because the graph doesn't show negative or positive and it can't be C because the graph is random therefore the graph is cannot be constant.
ANSWER ASAP PLS !!! CONSTRUCT ARGUMENTS Name the coordinates of the point at which the graphs of g(x)=2x+3 and h(x)=5x+3 intersect. Explain your reasoning.
Answers
The point of intersection is (0, 3). This means that the graphs of g(x) and h(x) intersect at the point where x=0 and y=3.
To find the point of intersection between the graphs of g(x)=2x+3 and h(x)=5x+3, we need to solve the equation g(x) = h(x) for x:
2x + 3 = 5x + 3
Subtracting 2x from both sides, we get:
3 = 3x + 3
Subtracting 3 from both sides, we get:
0 = 3x
Dividing both sides by 3, we get:
x = 0
So the graphs of g(x) and h(x) intersect at x = 0. To find the y-coordinate of the point of intersection, we can substitute x = 0 into either g(x) or h(x). Using g(x), we get:
g(0) = 2(0) + 3 = 3
To learn more about graphs here:
https://brainly.com/question/13690481
#SPJ1
A multiple-choice test has 5 questions each with 5 possible answers, the probability of guessing all the questions correctly is
Answers
In a multiple-choice test that has 5 questions, each with 5 possible answers, the probability of guessing all the questions correctly can be found using the formula:p = (1/5) × (1/5) × (1/5) × (1/5) × (1/5) = 1/3125.
The probability of guessing one question correctly is 1/5 since there are five possible answers. Since there are five questions, we multiply the probability by itself five times.
Therefore, the probability of guessing all the questions correctly is 1/3125, which is approximately 0.00032. This means that the chance of guessing all the questions correctly by random chance is very low.
This indicates that one should have studied for the test rather than relying solely on guesswork.
To learn more about probability, visit
brainly.com/question/13604758
#SPJ11
This is a Lesson 11 problem. This is an Exponential model problem. During the first week of registration, time between students adding Math 127 follows an Exponential model with a mean of 49 minutes. Determine the 20th percentile. Round your answer to four decimals. Example Answer: 2.2225
Answers
In an Exponential model problem where the time between students adding Math 127 follows an Exponential distribution with a mean of 49 minutes, we need to determine the 20th percentile.
In an Exponential distribution, the probability density function is given by f(x) = (1/μ) * e^(-x/μ), where μ is the mean of the distribution and x represents the time between events. To find the 20th percentile, we need to determine the value of x such that the cumulative probability up to x is 0.20. This can be achieved by using the cumulative distribution function (CDF) of the Exponential distribution.The CDF of an Exponential distribution is given by F(x) = 1 - e^(-x/μ).To find the 20th percentile, we need to solve the equation F(x) = 0.20 for x. Substituting the given mean μ = 49 into the equation, we have:
0.20 = 1 - e^(-x/49)
Rearranging the equation, we get:
e^(-x/49) = 0.80
Taking the natural logarithm (ln) of both sides, we have:
-ln(0.80) = -x/49
Solving for x, we find:
x = -49 * ln(0.80)
Using a calculator to evaluate the right-hand side of the equation, we get:
x ≈ 14.2875
Therefore, the 20th percentile of the time between students adding Math 127 is approximately 14.2875 minutes, rounded to four decimal places.
Learn more about cumulative probability here:- brainly.com/question/15070774
#SPJ11
find three consecutive numbers if their sum is 3n
Answers
Answer:
n-1,n,n+1
Step-by-step explanation:
let the numbers be x,x+1,x+2
x+x+1+x+2=3n
3x+3=3n
3x=3n-3
x=1/3 (3n-3)=n-1
so mumbers are n-1,n,n+1
The three consecutive numbers are n-1, n, and n+1.
We have to determine, the three consecutive numbers if their sum is 3n.
According to the question,
The consecutive number series can be even as well as odd depending on the first term of the series and the difference between the numbers.
Let, the three consecutive numbers be x, x+1, and x+2.
The sum of three consecutive numbers is equal to 33.
\(\rm x + x+1+x+2=3n\\\\3x+3 = 3n \\\\Divided \ by \ 3 \ on \ both \ the \ sides \\\\x +1 = n\\\\x = n-1\)
Therefore,
The first consecutive number is,
\(\rm x = n-1\)
The second consecutive number is,
\(\rm x+1 = n-1+1 = n\\\)
The third consecutive number is,
\(\rm x+2= n-1+2 = n+1\\\)
Hence, The three consecutive numbers are n-1, n, and n+1.
For more details refer to the link given below.
https://brainly.com/question/16048559
we want to distribute 7 flyers to 10 different mailboxes. how many ways can we do that if
Answers
There are 11,440 ways to distribute 7 identical flyers into 10 different mailboxes, where each mailbox receives at most one flyer.
If we are allowed to put at most one flyer per mailbox and the flyers are identical, this problem involves distributing identical objects into distinct containers. The solution can be obtained using the stars and bars method.
We can represent the distribution of flyers as 7 stars (representing the flyers) and 9 bars (representing the dividers between the mailboxes). The number of ways to distribute the flyers is equal to the number of ways to arrange the 7 stars and 9 bars, which is given by the binomial coefficient:
${{7 + 9}\choose{9}} = {{16}\choose{9}} = \frac{16!}{9!7!} = 11440$
Therefore, there are 11,440 ways to distribute 7 identical flyers into 10 different mailboxes, where each mailbox receives at most one flyer.
Learn more about combinatorics:https://brainly.com/question/28065038
#SPJ11
The question is incomplete but probably the full question is:
We want to distribute 7 flyers to 10 different mailboxes. How many ways can we do that if (a) We put at most one flyer per mailbox and the flyers are identical?