Answers
Answer: 120
Step-by-step explanation:
Since Angle formed at the center is equal to the angle measure of its opposite arc
⇒ ∠AOD = 104°
Also, The angle formed in the segment is half the angle formed at the center of the circle
⇒ ∠DOB = 2 × ∠BAD
⇒ ∠DOB = 2 × 68°
⇒ ∠DOB = 136°
Now, ∠AOB = 360 - ∠BOD + ∠AOD
⇒ ∠AOB = 360 - 136 - 104
⇒ ∠AOB = 120°
Now, Angle formed at the center is equal to the angle measure of its opposite arc
⇒ b = ∠AOB
⇒ b = 101°
Hence, the correct option is 120°
Related Questions
A scuba diver descends (goes down) to a location that is −10 m from sea level. He then descends (goes down) another -12 m. What is the scuba diver’s final location relative to sea level
Answers
Answer:
-22 m
Step-by-step explanation:
PLSSS HELP IF YOU TURLY KNOW THISS

Answers
7/8 is greater than 7/12
What is the average rate of change of the functionf(x)=20(14)x from x = 1 to x = 2? enter your answer, as a decimal, in the box. Do not round your answer.
Answers
The average rate of change of the function f(x) from x = 1 to x = 2 is, -3.75 when the function f(x)=20(1/4)ˣ.
Given that,
We have to find what is the function f(x)=20(1/4)ˣ average rate of change from x = 1 to x = 2.
We know that,
Average rate of change(A(x)) of f(x) over a interval [a,b] is given by:
A(x)=(f(b)-f(a))/b-a
We get the function:
f(x)=20(1/4)ˣ
Now, the average rate of change from x = 1 to x= 2
At x = 1
Then;
f(1)=20(1/4)¹=5
At x = 2
Then;
f(2)=20(1/4)²=1.25
Substitute these in above formula we have;
A(x)=f(2)-f(1)/2-1=-3.75
Therefore, The average rate of change of the function f(x) from x = 1 to x = 2 is, -3.75 when the function f(x)=20(1/4)ˣ.
To learn more about average visit: https://brainly.com/question/15397049
#SPJ4
A jewelry maker will use 24 jade beads and 30 teak beads to make necklaces. each necklace will have the same number of necklaces she can make? how many beads of each type are on each necklace?
Answers
The number of beads of each type that are on each necklace will be 6 beads.
How to illustrate the information?It should be noted that the jewelry maker will use 24 jade beads and 30 teak beads to make necklaces. each necklace will have the same number of necklaces she can make.
Therefore, it van be seen that the highest common factor between 24 and 30 is 6.
Therefore, the number of beads of each type that are on each necklace will be 6 beads.
Learn more about factors on:
brainly.com/question/25829061
#SPJ1
4. If a box of sweets is divided among 24 children, they will get 5 sweets each. How many would each get, if the number of the children is reduced by 4?
Answers
Between what two integers does log 2 1000 lie
Answers
Solution:
Given;
\(\log_21000\)From law of logarithm;
\(\log_ba=\frac{\log_{10}a}{\log_{10}b}\)Thus;
\(\begin{gathered} \log_21000=\frac{\log_{10}1000}{\log_{10}2} \\ \operatorname{\log}_21000=\frac{\operatorname{\log}_{10}10^3}{\operatorname{\log}_{10}2} \\ \end{gathered}\)Another law of logarithm;
\(\log_ba^c=c\log_ba\)Thus;
\(\begin{gathered} \log_21000=\frac{3\log_{10}10}{\log_{10}2} \\ \log_aa=1 \\ \log_21000=\frac{3\left(1\right)}{\log_{10}2} \\ From\text{ a table of common logarithm;} \\ \log_{10}2=0.3010 \\ \log_21000=\frac{3}{0.301} \\ \log_21000=\frac{3000}{301} \\ \log_21000=9\text{ remainder 291} \\ \end{gathered}\)FINAL ANSWER
\(\log_21000\text{ lies between }9\text{ and }10\)
Please help!!! I’m really confused and need help

Answers
The slope of the linear equation is -5/2, thus, the correct option is B.
What is the slope of the line?A general line can be written in the slope-intercept form as:
y = a*x + b
Where a is the slope.
Here we have the linear equation:
5x + 2y = 9
If we isolate y we will get:
2y = 9 - 5x
y = 9/2 - (5/2)*x
y = (-5/2)x + 9/2
then we can see that the slope is -5/2, so the correct option is B.
Learn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
which number will make the two fractions equivalent 42/50 84/?
Answers
Answer:
Step-by-step explanation:
84 is twice 42
Multiply the numerator and the denominator of 42/50 by 2:
42/50 = (42×2)/(50×2) = 84/100
Answer:
84/100
Step-by-step explanation:
84 is twice 42 Multiply the numerator and the denominator of 42/50 by 2: 42/50 = (42×2)/(50×2) = 84/100
Robin has read 3/4
of a book. Mark said he had read 1/2
as much as Robin. What fraction of the book has Mark ready?
Answers
Answer:
3/8
Step-by-step explanation:
Answer:
3/8
Step-by-step explanation:
3/4 × 1/2 = 3/8I hope this helps!
help me with this question please

Answers
Answer:
N+1
Step-by-step explanation:
It begins with = 2
then n+1=3
then n+2=4 and so on it is n+1
please help me , I need help!!!
P is an odd number. Q is an even number. Explain why P × Q + 1 is always an odd number?
Answers
Answer:
An odd number times an even number is always even
e.g 2 × 3 = 6
4 × 5 = 20
adding 1 to an even number makes it odd
6 + 1 = 7
20 + 1 = 21
hope this helps...
Answer:
P is an odd number
Q is an even number
Now, product of a odd number and even number is always even number.
Therefore, P×Q is a even number
Now, by adding 1 to the even number it becomes odd.
Hence, P×Q+1 is always an odd number.
subtracting 9 From A Certain number gives 13 what is the number
Answers
Answer:
22
Step-by-step explanation:
N-9=13
N-9+9=13+9
N=22
Answer:
the answer for the question is 22
Step-by-step explanation:
as I said,a certain number =x
therefore,x-9=13
x=13+9
x=22
pleawe help kqkakakakakakaka

Answers
Answer:
-16
Step-by-step explanation:
ez if not u baka
Answer:
use the raditon theroem, 24x^2025x/ax-2 mulitplied by tan is equal to A)-16
The equation p = 3.25b can be used to find the price, p, in dollars, of b pounds of blueberries at a particular supermarket. Each of the tables gives the prices of various pounds of blueberries at a different supermarket. Which of these tables represents blueberries that are more expensive than those represented by the equation? Select all that apply.

Answers
Answer:
Table C, Table D, Table E
Step-by-step explanation:
See attachment for tables
Given
\(p = 3.25b\)
Required
Which of the tables is more expensive than the given function
To answer this question, we simply determine the equation of each table and then compare the equation with \(p = 3.25b\)
Table A:
Consider two corresponding points in the table, we have:
\((b_1,p_1) = (1,2.75)\)
\((b_2,p_2) = (4,11)\)
Determine the slope
\(m = \frac{p_2 - p_1}{b_2 - b_1}\)
\(m = \frac{11 - 2.75}{4 - 1}\)
\(m = \frac{8.25}{3}\)
\(m = 2.75\)
The equation is determined as follows:
\(p - p_1 = m(b-b_1)\)
\(p - 2.75 = 2.75(b-1)\)
\(p - 2.75 = 2.75b-2.75\)
\(p = 2.75b\)
Comparing this equation to \(p = 3.25b\), we have that:
\(2.75 < 3.25\)
Hence:
This equation is less expensive than \(p = 3.25b\)
Table B:
Consider two corresponding points in the table, we have:
\((b_1,p_1) = (1.5,3.75)\)
\((b_2,p_2) = (6,15)\)
Determine the slope
\(m = \frac{p_2 - p_1}{b_2 - b_1}\)
\(m = \frac{15 - 3.75}{6 - 1.5}\)
\(m = \frac{11.25}{4.5}\)
\(m = 2.5\)
The equation is determined as follows:
\(p - p_1 = m(b-b_1)\)
\(p - 3.75 = 2.5(b-1.5)\)
\(p - 3.75 = 2.5b- 3.75\)
\(p = 2.5b\)
Comparing this equation to \(p = 3.25b\), we have that:
\(2.5 < 3.25\)
Hence:
This equation is also less expensive than \(p = 3.25b\)
Table C:
Consider two corresponding points in the table, we have:
\((b_1,p_1) = (2,7)\)
\((b_2,p_2) = (4,14)\)
Determine the slope
\(m = \frac{p_2 - p_1}{b_2 - b_1}\)
\(m = \frac{14 - 7}{4 - 2}\)
\(m = \frac{7}{2}\)
\(m = 3.5\)
The equation is determined as follows:
\(p - p_1 = m(b-b_1)\)
\(p - 7 = 3.5(b - 2)\)
\(p - 7 = 3.5b - 7\)
\(p = 3.5b\)
Comparing this equation to \(p = 3.25b\), we have that:
\(3.5 > 3.25\)
Hence:
This equation is more expensive than \(p = 3.25b\)
Table D:
Consider two corresponding points in the table, we have:
\((b_1,p_1) = (2.5,10)\)
\((b_2,p_2) = (5,20)\)
Determine the slope
\(m = \frac{p_2 - p_1}{b_2 - b_1}\)
\(m = \frac{20 - 10}{5 - 2.5}\)
\(m = \frac{10}{2.5}\)
\(m = 4\)
The equation is determined as follows:
\(p - p_1 = m(b-b_1)\)
\(p - 10 = 4(b - 2.5)\)
\(p - 10 = 4b - 10\)
\(p = 4b\)
Comparing this equation to \(p = 3.25b\), we have that:
\(4 > 3.25\)
Hence:
This equation is more expensive than \(p = 3.25b\)
Table E:
Consider two corresponding points in the table, we have:
\((b_1,p_1) = (6, 22.5)\)
\((b_2,p_2) = (12,45)\)
Determine the slope
\(m = \frac{p_2 - p_1}{b_2 - b_1}\)
\(m = \frac{45 - 22.5}{12 - 6}\)
\(m = \frac{22.5}{6}\)
\(m = 3.75\)
The equation is determined as follows:
\(p - p_1 = m(b-b_1)\)
\(p - 22.5 = 3.75(b - 6)\)
\(p - 22.5 = 3.75b - 22.5\)
\(p = 3.75b\)
Comparing this equation to \(p = 3.25b\), we have that:
\(3.75>3.25\)
Hence:
This equation is more expensive than \(p = 3.25b\)
Table F:
Consider two corresponding points in the table, we have:
\((b_1,p_1) = (7, 21)\)
\((b_2,p_2) = (14,42)\)
Determine the slope
\(m = \frac{p_2 - p_1}{b_2 - b_1}\)
\(m = \frac{42 - 21}{14 - 7}\)
\(m = \frac{21}{7}\)
\(m = 3\)
The equation is determined as follows:
\(p - p_1 = m(b-b_1)\)
\(p -21 =3(b -7)\)
\(p -21 =3b -21\)
\(p = 3b\)
Comparing this equation to \(p = 3.25b\), we have that:
\(3 < 3.25\)
Hence:
This equation is less expensive than \(p = 3.25b\)

1 half times 2 / 6 times six plus four
Answers
\( \bold{answer \: \: \to} \\ 1\frac{1}{2} \times \frac{2}{6} \times \frac{6}{1} + 4 = \\ = \frac{3}{2} \times \frac{1}{3} \times \frac{6}{1} + 4 \\ = \frac{3}{6} \times \frac{6}{1} + 4 \\ \ = \frac{18}{6} + 4 \\ = 3 + 4 \\ = \boxed{ \bold{7}}\)
evaluate ∮cxdx ydyx2 y2, where c is any jordan curve whose interior does not contain the origin, traversed counterclockwise. ∮cxdx ydyx2 y2=
Answers
The value of the line integral ∮c x dx + y dy / \((x^2 + y^2)\), where c is any Jordan curve whose interior does not contain the origin, traversed counterclockwise, is 0.
To evaluate the line integral ∮c x dx + y dy / \((x^2 + y^2)\), where c is any Jordan curve whose interior does not contain the origin, traversed counterclockwise, we can apply Green's theorem.
Green's theorem states that for a vector field F = P(x, y) i + Q(x, y) j, and a simple closed curve C with positively oriented boundary, the line integral of F along C is equal to the double integral of the curl of F over the region enclosed by C.
In this case, the vector field F = x i + y j, and the line integral becomes ∮c x dx + y dy / \((x^2 + y^2)\) = ∬R curl(F) dA.
The curl of F is given by curl(F) = (∂Q/∂x - ∂P/∂y) k = (1 - 1) k = 0.
Since the curl of F is zero, the line integral becomes ∬R 0 dA = 0.
Therefore, the value of the line integral ∮c x dx + y dy / \((x^2 + y^2)\), where c is any Jordan curve whose interior does not contain the origin, traversed counterclockwise, is 0.
To learn more about line integral from the given link
https://brainly.com/question/31421669
#SPJ4
Hi, can you help me to solve this exercise, please!

Answers
Trigonometric Identities.
To solve this problem, we need to keep in mind the following:
* The tangent function is negative in the quadrant II
* The cosine (and therefore the secant) function is negative in the quadrant II
* The tangent and the secant of any angle are related by the equation:
\(\sec ^2\theta=\tan ^2\theta+1\)We are given:
\(\text{tan}\theta=-\frac{\sqrt[]{14}}{4}\)And θ lies in the quadrant Ii.
Substituting in the identity:
\(\begin{gathered} \sec ^2\theta=(-\frac{\sqrt[]{14}}{4})^2+1 \\ \text{Operating:} \\ \sec ^2\theta=\frac{14}{16}+1 \\ \sec ^2\theta=\frac{14+16}{16} \\ \sec ^2\theta=\frac{30}{16} \end{gathered}\)Taking the square root and writing the negative sign for the secant:
\(\begin{gathered} \sec ^{}\theta=\sqrt{\frac{30}{16}} \\ \sec ^{}\theta=-\frac{\sqrt[]{30}}{4} \end{gathered}\)Use algebra tiles to multiply (x - 1)(3x + 2).
Answers
Answer:
Step-by-step explanation:
543
In the figure, O is the centre of the semicircle at E. If AD BC and ZACB=30°, then 80°. 85°. 90°. 95°. А. B. C. D. ABCD. It is given that OB and AC intersect ZCEO =
Answers
The angle ZCEO is 90°.
In the given figure, O is the center of the semicircle at E. We are given that AD is parallel to BC, and the angle ZACB is 30°.
To find the value of angle ZCEO, we need to consider the properties of angles in a circle and the relationship between angles formed by intersecting lines.
First, let's focus on the angle ZACB. Since AD is parallel to BC, the angle ZACB is equal to the angle ZBC.
In a circle, the angle subtended by an arc at the center is twice the angle subtended by the same arc at any point on the circumference. Therefore, angle ZEO is equal to 2 * angle ZCB.
Since angle ZACB is given as 30°, angle ZCB is also 30°. Therefore, angle ZEO is 2 * 30° = 60°.
Now, we consider the angle ZEOC. The angles around a point add up to 360°. So, angle ZEOC = 360° - angle ZEO = 360° - 60° = 300°.
Finally, we know that angle ZCEO is the exterior angle formed by the intersection of OB and AC.
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two opposite interior angles.
In this case, angle ZCEO is equal to angle ZEOC + angle ZACB = 300° + 30° = 330°.
Therefore, the angle ZCEO is 330°.
To learn more about interior angles visit:
brainly.com/question/2125016
#SPJ11
Suppose that the relationship between a response variable y and an explanatory variable x is modeled by y = 2.7(0.316)^x.
Which of the following scatterplots would be approximately follow a straight line?
a.) A plot of y against
b.) A plot of y against log x
c.) A plot of log y against x
d.) A plot of log y against log x
e.) None of the above
Answers
The scatterplot that would be approximately follow a straight line is c.) a plot of log y against x.
Taking the logarithm of y transforms the model to log y = log 2.7 + x log 0.316, which is a linear function of x. Therefore, plotting log y against x would result in a linear relationship, where the slope of the line is the logarithm of 0.316 and the intercept is the logarithm of 2.7.
The other options do not result in a linear relationship when plotted. A plot of y against x would result in a curve, a plot of y against log x would result in an exponential curve, a plot of log y against log x would result in a power law relationship. Therefore, the correct answer is c).
For more questions like Scatterplot click the link below:
https://brainly.com/question/29366075
#SPJ11
in the figure, m∠7 = 100°. find the measure of each angle.

Answers
Step-by-step explanation:
Those are angles formed by the parallel side and intersectected line so their adjecent angles are suplement ( their sum 180°) and their opposite angles are congrunt.
So
<1 =<3= <5=<7=<9=<11 ... by vertical oppo. angle theorem
<2=<4=<6=<8=<10 = <12 ... by vertical oppo. angle theorem too
Now our given is <7 = 100° so they are equal to <1 =<3= <5=<9=<11 and they are suplement to <6 = 80°
so <2=<4=<8=<10 they are equal .
find all the local maxima, local minima, and saddle points of the function. f(x,y) = x^3-18xy y^3
Answers
The partial derivatives of the function with respect to x and y are both zero at the critical point (0,0), which is a saddle point.
The local maxima, local minima, and saddle points of the function f(x,y) = \(x^3 - 18xy y^3\), we need to take the partial derivatives of the function with respect to x and y and set them equal to zero.
First, we can find the critical points of the function by setting the partial derivatives equal to zero:
\(x^3 - 18xy y^3 = 0\)
Taking the partial derivative of \(x^3\) with respect to x, we get:
\(3x^2 = 18xy\)
Taking the partial derivative of \(y^3\) with respect to y, we get:
\(3y^2 = -18x\)
Now, we can set these equal to zero and solve for x and y:
\(3x^2 = 18xy\\x^2 = 6y\\3y^2 = -18x\\y^2 = -6x\)
Substituting these expressions for x and y into the previous equation, we get:
6y = 6y
y = 0
\(x^2 = 6(0)\\x^2 = 0\)
Therefore, the critical points of the function are (0,0), which correspond to a saddle point.
To check that this is a saddle point, we can calculate the Jacobian matrix of the function at this point:
J(0,0) = [3, 6]
The determinant of the Jacobian matrix is 3, which is positive. Therefore, the critical point (0,0) is a local minimum.
Since the critical point (0,0) is a saddle point, it is also a local maximum.
Next, we can find the partial derivatives of the function with respect to x and y at the critical point:
\(x^3 - 18xy y^3 = 0\)
\(3x^2 = 18xy\\3y^2 = -18x\)
At the critical point (0,0), we have:
x = 0
y = 0
The partial derivatives, we get:
0 = 18(0)y
y = 0
Substituting this value of y into the partial derivative of \(x^3\) with respect to x, we get:
0 = 0
Therefore, the partial derivatives of the function with respect to x and y are both zero at the critical point (0,0), which is a saddle point.
Learn more about partial derivatives visit: brainly.com/question/30217886
#SPJ4
Determine whether the binomial (x-4) is a factor of the polynomial p(x) = 5x³ - 20x² - 5x+ 20-
Answers
Step-by-step explanation:
IF x-4 is a factor, then putting in x = + 4 will make the polynomial = 0
5 ( 4^3) - 20 (4^2) - 5(4) + 20 = 0 Yes...it is a factor
\(x - 4 = 0 \\ x = 4 \\ \)
substitute value of x in the function to see if it equals to zero , if not it won't be a factor of the function
\(5 {x}^{3} - 20 {x}^{2} - 5x + 20 = 0 \\ 5(4) ^{3} - 20( {4})^{2} - 5(4) + 20 = 0 \\ 5(64) - 20(16) - 20 + 20 = 0 \\ 320 - 320 - 20 + 20 = 0 \\ 0 = 0\)
so (x-4) is a factor for the function
What is the solution to this system of equations?
x = 12 − y
2x + 3y = 29
Answers
x+y=12
2x+3y=29
Multiply equation 1 by 2
So it will be
2x+2y=24
Subtract eq 1 from eq 2
2x+3y=29
2x+2y=24
—————-
Y =5
Put value of y in eq 1
2x+2y=24
2x +10= 24
2x= 24-10
2x= 14
x=14/2
x=7
S.S= (7,5)
Explanation: I would use the substitution method for this system
because one of the variables, x, is already isolated in the first equation.
Since our first equation states that x = 12 - y, 12 - y can be substituted
in for x in the second equation which becomes 2(12 - y) + 3y = 29.
Now we can solve this equation by first distributing the 2
through the parentheses to get 24 - 2y + 3y = 29 and you
should be able to easily finish solving from here to get y = 5.
Now substitute a 5 back in for the first equation to get
x = 12 - (5) or x = 7 which means that our solution is (7, 5).
Help with geometry please

Answers
X=30
Z is equal to 3x-10
So z=80
80+42= 122
180-122= 58 (angle C)
Y = 122 because angles on a straight line add up to 180
which fraction is equal to 0.03 repating?
A) 3/100
B)1/33
C)1/11
D)1/3
Answers
Answer:
B
Step-by-step explanation:
A = 0.03, not repeating So it's not A
B = 0.03030303... So It's correct
C = 0.0909090... So it's wrong
D = 0.33333333... It's not 0.03030303...
B is the correct answer. If this helped, please mark me as Brainliest. Thank you and have a nice day.
solve the equation 4/5x-2 = x
Answers
Answer:
\(\frac{4}{5}\)x-2=x
\(\frac{4x}{5}\)-2=x
\(\frac{4x}{5}\)+\(\frac{5(-2)}{5}\)=x
\(\frac{4x+5(-2)}{5}=x\)
x= -10
Step-by-step explanation:
2. Formulate the following problems as a pair of equations, and hence find their solutions: (1) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
Answers
Answer:
her speed in still water = 11 km/hour
the speed of the current = 9 km/hour
Step-by-step explanation:
x = Ritu's speed of rowing.
y = the sites of the river water flowing
x + y = 20 km / 2 hours = 10 km / hour
x - y = 4 km / 2 hours = 2 km / hour
x = 2 + y
2 + y + y = 20
2y = 18
y = 9 km/hour
x = 2 + y = 2 + 9 = 11 km/hour
Speed of water while upstream is (x + y) km/hr,
downstream is (x – y) km/hr,
2(x + y) = 20 x + y = 10 ………… (i)
2(x – y) = 4 x – y = 2 …………… (ii)
By Adding eqn. (i) and eqn.x + y = 10
x - y = 2
_______________
x = 12
\(x = \frac{12}{2} = 6\)
(ii), Substituting the value,
x = 6 in eqn.(i), x + y = 10 6 + y = 10 y = 10 – 6
∴ y = 4
∴ Speed of Ritu in still water, x = 6 km/hr. in current water, y = 4 km/hr.
a sphere is inscribed in a cylinder use complete sentences and geometric formulas to compare the surface area of the sphere and the lateral area of the cylinder
Answers
Answer:
They are the same
Step-by-step explanation:
LA cyl =
\(2\pi \: rh\)
SA sphere =
\(4\pi {r}^{2} \)
If the sphere is inscribed in the cylinder, they have the same radius. The height of the cylinder is the diameter (Or 2× radius) of the sphere.
If you substitute 2r for h, then both formulas are
\( 4\pi{r}^{2} \)
Solve For The Variable

Answers
Answer:
115.2
Step-by-step explanation:
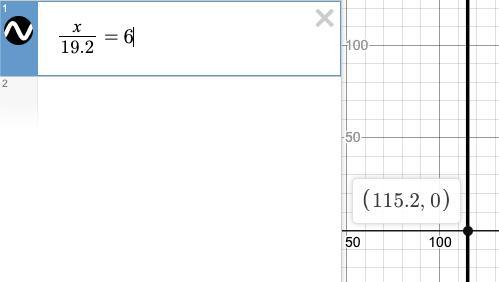
Answer:
x=115.2
Step-by-step explanation:
Multiply both sides by 19.2 to clear the fraction.
19.2*6=115.2
