Answers
Answer:
72°
Explanation:
Given that line J and line K are parallel, we can safely assume that line m is the transversal for the following question. We can also remove line l so that we can focus on line m instead.
Using the rule of Alternate Exterior Angle theorem, x would equal to 72°.
Answer: 72
Now that we are told that J and K are parallel, we know that there can be a transversal line (m). You can see that m goes 72 degrees.
So, the answer is 72. Best of Regards!
Related Questions
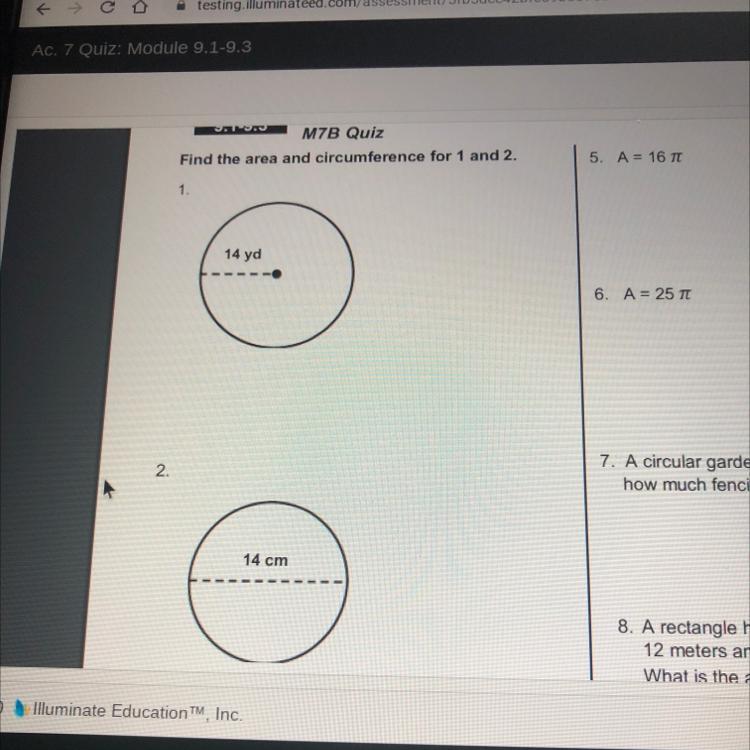
Find the area and circumference for 1 and 2.
5. A
1.
14 yd
6.
Answers
a metal plate with the boundary temperatures as below. Use Guass-Jordas tion to estimate the temperatures w, x, y, z at each of the four interior point steel plate shown in the figure. Assume, in each case, that the temperatur nterior point is approximated by the average of the temperatures at the fou points.
Answers
Using Gauss-Jordan elimination, we can estimate the temperatures w, x, y, and z at the four interior points of the steel plate based on the given boundary temperatures.
To estimate the temperatures at the interior points, we can set up a system of linear equations based on the given boundary temperatures. Let's denote the temperatures at the interior points as w, x, y, and z. Each interior point's temperature can be approximated as the average of the temperatures at the four surrounding points.
We can then write the following equations:
w = (30 + x + y) / 3
x = (20 + w + z) / 3
y = (10 + w + z) / 3
z = (40 + x + y) / 3
Rearranging these equations, we get:
3w - x - y = 30
-w + 3x - z = 20
-w + 3y - z = 10
-x - y + 3z = 40
We can solve this system of equations using Gauss-Jordan elimination or any other suitable method to find the values of w, x, y, and z, which will give us the estimated temperatures at the interior points of the steel plate.
Learn more about Gauss-Jordan elimination click here :brainly.com/question/21088742
#SPJ11
look below !!!! !!!!!!!!!!

Answers
Answer:
5/4 is the answer
Step-by-step explanation:
does someone mind helping me with this problem? Thank you!

Answers
The quotient of the value to the nearest tenth is 4791.7
Division of valuesAccording to the question we are to solve the division expression
345.00/0.072
Convert the decimal to fraction
0.072 = 72/1000
Substitute
345.00/0.072 = 345÷(72/1000)
345.00/0.072 = 345* 1000/72
345.00/0.072 = 345000/72
345.00/0.072 = 4791.7
Hence the quotient of the value to the nearest tenth is 4791.7
Learn more division here: https://brainly.com/question/25289437
#SPJ1
help asap please , don’t know how to do this lol

Answers
Answer:
no
Step-by-step explanation:
based only on the information given in the diagram, which conference theorems or postulates could be given as reasons why AABC = AXYZ?

Answers
The congruence theorems or postulates that could be given as reasons for ΔABC = ΔXYZ is SAS.
Option C is the correct answer.
We have,
Side-Angle-Side (SAS) Congruence.
The two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle.
Now,
ΔABC and ΔXYZ
AC = XZ (corresponding side)
∠ACB = ∠XZY ( corresponding angle)
BC = YZ (corresponding sides)
This means,
Side Angle Side
Thus,
The congruence theorems or postulates that could be given as reasons for ΔABC = ΔXYZ is SAS.
Learn more about triangle congruency here:
https://brainly.com/question/12413243
#SPJ1
Say NANI and will give a lot of points
Answers
Determine the coefficients of the complex exponential Fourier series of the following signals: (i) x(t) = 1 + cos(2t) + cos(8t + π/2) (ii) x(t) = 2 sin(t) + 3 cos(3t+ π/3)
Answers
The complex exponential Fourier series of a signal can be determined by computing the coefficients A₀ and Aₙ.
For (i), the complex exponential Fourier series is given by:
X(ω) = A₀ + ∑[Ancos(nωt + φn) ], where
A₀ = 1/2
Aₙ = (1/2)[cos(2nπ/8) + cos(2nπ/8 + π/2)]
For (ii), the complex exponential Fourier series is given by:
X(ω) = A₀ + ∑[Ancos(nωt + φn) ], where
A₀ = 1
Aₙ = (2/2)[sin(nπ/3) + 3cos(nπ/3 + π/3)]
In conclusion, the complex exponential Fourier series of a signal can be determined by computing the coefficients A₀ and Aₙ. This technique can be used to analyze any periodic signal or system and is invaluable in signal processing, communications, and control engineering.
To know more about Fourier series, click-
https://brainly.com/question/30763814
#SPJ11
Jennifer made these measurements on ABC,BC must be-?

Answers
Answer:
between 10 and 12
Step-by-step explanation:
Given the measure of angles:
m∠B = 70°
m∠C = 60°
m∠A = 50°
We know m∠B = 70° because the sum of interior angles in a triangle is equal to 180°.Following this information, since the side lengths are directly proportional to the angle measure they see:
Angle B is the largest angle. Therefore, side AC is the longest side of the triangle since it is opposite of the largest angle.
Angle C is the smallest angle, so the side AB is the shortest side.
Therefore, side BC must be between 10 and 12 inches.
What is the effect on the graph of the function f(x) = x2 when f(x) is changed to f(x − 6)?
Answers
Answer:
Horizontal translation in the \(+x\) direction.
Step-by-step explanation:
A function of the form \(f(x)\) experiments an horizontal translation when the following substitution is applied:
\(x \to x + a\), where \(a \in \mathbb{R}\)
If \(a > 0\), the function is translated in the \(-x\) direction, whereas \(a < 0\) is the case for the function being translated in the \(+x\) direction.
The effect on the graph can be defined by a composition between two function:
\(f(x) = x^{2}\), \(g (x) = x-6\)
\(f\,\circ\,g\,(x) = (x-6)^{2}\)
The resulting expression represents a horizontal translation in the \(+x\) direction.
Finally, we plot \(f(x)\) (red) and \(f\,\circ g\,(x)\) (blue) by a graphing tool and proved the certainty of this theory.

Someone please help me thank you

Answers
Answer:
4
Step-by-step explanation:
7x = x² - 8
=> x² - 7x - 8 = 0
use quadratic formula:
a = 1, b = -7, c = -8
x = \(\frac{-(1)±\sqrt{(-7)^{2} - 4(1)(-8) } }{2(1)}\) (pls ignore the "A" I don't know why it's showing up)
=> x = \(\frac{-1±\sqrt{49 + 32} }{2}\)
=> x = \(\frac{-1±9 }{2}\)
=> x = \(\frac{-1 +9}{2}\) = 4 or \(\frac{-1-9}{2}\) = -5 (the answer is only 4 since it's asking for the positive solution)

PLEASE HELP WILL GIVE BRAINLIEST SIMPLIFY THE FOLLOWING EXPRESSION I NEED BOTH

Answers
Answer:
First one- 1/5^2
Second- 2/3m^15
Step-by-step explanation:
What is the interquartile range of this data set ?

Answers
Step-by-step explanation:
A. ayan po ang sagut nag check napo kami kase yan eh sige po.welcome
HELP PLS!!!
Find the surface area of the pyramid.

Answers
well, the hexagonal pyramid is really just six triangles with a base of 24 and a height of 24 as well, and a hexagonal base with an apothem of 12√3 and sides of 24.
\(\textit{area of a regular polygon}\\\\ A=\cfrac{1}{2}ap ~~ \begin{cases} a=apothem\\ p=perimeter\\[-0.5em] \hrulefill\\ a=12\sqrt{3}\\ p=\stackrel{(24)(6)}{144} \end{cases}\implies A=\cfrac{1}{2}(12\sqrt{3})(144) \\\\[-0.35em] ~\dotfill\\\\ \stackrel{ \textit{\LARGE Areas} }{\stackrel{\textit{six triangles}}{6\left[ \cfrac{1}{2}(\underset{b}{24})(\underset{h}{24}) \right]}~~ + ~~\stackrel{\textit{hexagonal base}}{\cfrac{1}{2}(12\sqrt{3})(144)}}\implies 1728+864\sqrt{3} ~~ \approx ~~ \text{\LARGE 3224}~m^2\)
(7.3^3-sqrt 3•5+7^2)^2
Answers
Answer:
I cannot answer that but here is an example problem to help.
Step-by-step explanation:

Measure the length of each leg and the hypotenuse.
m∠ABC = 45° m∠ACB = 45°
Question:
AB =? Units
AC =? Units
BC =? Units
Answers
The hypotenuse, AC, is equal to the length of a leg multiplied by √2. , AC = x√2 units.
To summarize:
AB = BC = x units
AC = x√2 units
In a right triangle where one angle is 45°, we can determine the lengths of the legs and the hypotenuse using the properties of a 45-45-90 triangle.
In a 45-45-90 triangle, the two legs are congruent, and the hypotenuse is equal to the length of a leg multiplied by √2.
Let's assume the length of one leg is "x" units.
Since m∠ABC = 45° and m∠ACB = 45°, we can conclude that AB and BC are congruent. So, AB = BC = x units.
The hypotenuse, AC, is equal to the length of a leg multiplied by √2. Therefore, AC = x√2 units.
To summarize:
AB = BC = x units
AC = x√2 units
For such more questions on Legs and Hypotenuse Lengths
https://brainly.com/question/29258809
#SPJ8
pls help i think this is pass due and i need this done

Answers
Answer:
c. 29.3 cubic mi.
Step-by-step explanation:
Volume of cone: \(\pi\) × r² × \(\frac{h}{3}\)
Volume of cone = \(\pi\) × 2² × \(\frac{7}{3}\)
= 9\(\frac{1}{3}\)\(\pi\)
= 29.3 cubic mi. (rounded to 3 s.f.)
Pythagorean Theorem & irrational Numbers Question
Which of the following could not be the lengths of sides of a
right triangle?
Select one:
8, 10, 12
6, 8, 10
9, 12, 15
8, 15, 17
Answers
Answer:
2nd
Step-by-step explanation:
given rectangleWXYZ with m angle W = 4n + 5 and m angle Y = 3n + 21. What is the measure of angle W
Answers
Answer:
Given,
WXYZ is a rectangle.
All angles are equal.
Each angle is a right angle.
angleW = 90°
Step-by-step explanation:
Given,
WXYZ is a rectangle.
All angles are equal.
Each angle is a right angle.
angleW
\( = 4n + 5 = 90\)
\(4n = 90 - 5\)
\(4n = 85\)
\(n = \frac{85}{4} \)
angleW
\(4n + 5\)
\(4 \times\frac{85}{4} + 5\)
\(85 + 5\)
\(90\)
Without actually solving the given differential equation, find the minimum radius of convergence R of power series solutions about the ordinary point x = 0 . About the ordinary point x = 1 . ( x^2 − 2x + 17 )y ′′ + xy ′ − 4y = 0
Answers
The minimum radius of convergence R of power series solutions about the ordinary point x = 0 is 4.123 and that about the ordinary point x = 1 is 4 units.
What is radius of convergence?
In mathematics, the radius of convergence of a power series is stated as the radius of the largest disk at the center of the series in that the series converges. Radius of convergence is either a non-negative real number or infinity.
The given differential equation is
(x² -2x+17) y" +xy' -4y =0
We have to find the minimum radius of convergence R of power series solutions about the ordinary point x = 0 and x = 1.
The minimum radius of convergence can be defined as the distance between the ordinary point and the singularity of the differential equation.
Singularity point is the root of the polynomial attached with the second derivative. So, the singularity points can be calculated as,
(x² -2x+17)=0 Comparing this with ax²+bx+c=0 we get,
x=\(\frac{-b+\sqrt{b^{2} -4ac } }{2a}\) and x= \(\frac{-b-\sqrt{b^{2} -4ac } }{2a}\)
x= \(\frac{2+\sqrt{4 -68 } }{2}\) and x= \(\frac{2-\sqrt{4 -68 } }{2}\)
x= (2±8i)/2
x= 1±4i
So, the singularity points are x₁= 1+4i and x₂ = 1-4i
Now, the ordinary points can be written as z₁= 0+0i and z₂ = 1+0i
The minimum radius of convergence can be calculated as,
r₁ = | z₁ - x₁ |
= | 0+0i-1-4i |
= | -1-4i |
= √17
= 4.123
r₂ = | z₂ - x₂ |
= | 1+0i-1+4i |
= | 4i |
= √16
= 4
Hence, the minimum radius of convergence R of power series solutions about the ordinary point x = 0 is 4.123 and that about the ordinary point x = 1 is 4 units.
To know more about radius of convergence
https://brainly.com/question/17193241
#SPJ4
Find the perimeter of this figure. Enter your answer in the box.
(-7 , 3) (8 , 3) (-7 , -1) (2 , -1) (2 , -8) (8 , -8)
Answers
Answer:
56 total units
Step-by-step explanation:
Here is what the plane would look like if the figure and points were drawn.

Answer:
52 unitsStep-by-step explanation:
Plot the points and connect.
Note. If you connect the points in the given order you will end up with a weird figure hence we connect as pictured.
Horizontal sides sum to:
2*(8 - (-7)) = 2*15 = 30Vertical sides sum to:
2*(8 - (-3)) = 2*11 = 22The perimeter is:
30 + 22 = 52
For the following exercises, determine whether the equation represents exponential growth, exponential decay, or neither. Explain. 1. y = 12.25(x)³
Answers
The given equation y = 12.25(x)³ represents a exponential growth.
Exponential growth occurs when the base of the exponent is greater than 1, resulting in the function increasing as x increases.
Exponential decay occurs when the base of the exponent is between 0 and 1, causing the function to decrease as x increases.
We need to examine the exponent, which is (x)³.
In an exponential growth function, the base (in this case, x) is raised to a positive exponent, resulting in an increase in the output value (y) as x increases.
In the given equation, the base x is raised to the power of 3.
This means that as x increases, the function y will increase rapidly since raising x to the power of 3 amplifies its effect.
This behavior is indicative of exponential growth.
To learn more on Functions click:
https://brainly.com/question/30721594
#SPJ4
ar function, and/or a
2.
Which set of ordered pairs represents a function?
A ((-20,30),(-40,0),(-40,50))
B ((-30,0), (-30, 20), (-30,50)}
C {(-40,0), (20,-30), (60,-50)}
D ((-50,0), (20,-30), (-50,60)}
Answers
{(-40,0), (20,-30), (60,-50)} relation is a function.
What is a function?A relation is a function if it has only One y-value for each x-value.
A relation between two sets is a collection of ordered pairs containing one object from each set
The ordered pairs are
((-20,30),(-40,0),(-40,50))
The relation is not a function as -40 is repeated two times
((-30,0), (-30, 20), (-30,50)}
The relation is not a function as -30 is repeated three times
{(-40,0), (20,-30), (60,-50)}
The relation is a function because every y value has unique x value.
((-50,0), (20,-30), (-50,60)}
The relation is not a function as -50 is repeated two times.
Hence {(-40,0), (20,-30), (60,-50)} relation is a function.
To learn more on Functions click:
https://brainly.com/question/21145944
#SPJ1
if the equation mx²+5x+2=0 and 3x²+10x+n =0 have a common root, find the value of m and n
Answers
The value of the variables m and n are 3/2 and 4 respectively
How to determine the valueNoe that quadratic functions are defined as functions having its degree as 2.
The general formula for a quadratic function is expressed as;
ax² + bx + c
Standard form
ax² + bx + c = 0
Given the illustration, we have that the two functions have similar roots.
Then, we have;
The value of n = 4
For the value of m, we represent it thus; (-b/a)
-5x/m = -10x/3
cross multiply the values, we get;
m = 3(-5x)/-10x
m = 3/2
Learn about quadratic functions at: https://brainly.com/question/25841119
#SPJ1
Use the bar graph to answer the question.
What was the third most favorite communication method chosen?
Question 2 options:
A.cell phone call
B.e-mail
C.instant message
D.cell phone text

Answers
Answer:
A
Step-by-step explanation:
the graph shows It's the 3rd tallest
A line passes through (12,-4) and (-6,10). Find the y-intercept, b, of the line.
Answers
The y-intercept of the line passes through (12,-4) and (-6,10) is 32/6
Let (x1, y1) = (12, -4)
and (x2, y2) = (-6, 10)
Using the formula of the two-point form of equation of line,
(y - y1)/(y2 - y1) = (x - x1)/(x2 - x1)
(y + 4)/(10 + 4) = (x - 12)/(-6 - 12)
(y + 4)/14 = (x - 12)/(-18)
-18y -72= 14x - 168
-18y = 14x - 168 + 72
-18y = 14x - 96
y = -(14/18)x + 96/18
y = -7/9 x + 32/6
Comparing with slope-intercept form of line y = mx + b
y-intercept(b) = 32/6
Therefore, the y-intercept of the line passes through (12,-4) and (-6,10) is 32/6
Learn more about the y-intercept here:
https://brainly.com/question/14180189
#SPJ1
por favor please help D:
Answers
Answer:
Im looking around and I dont see anything :C
Step-by-step explanation:
Sorry I could not help!
-Ella-
a medical school claims that more than 28% of its students plan to go into general practice. it is found that among a random sample of 130 of the school's students, 32% of them plan to go into general practice. find the p-value for a test of the school's claim. group of answer choices
Answers
The school's claim group of answer options has a p-value for a test of 0.1539.
The notation and data are provided.
The sample is chosen at random: n = 130
The estimated proportion of students who intend to pursue general practice is: \(\bar p = 32\% = \frac{28}{10} = 0.32\)
The value to be tested is: p₀ = 28% = 28/100 = 0.28
The statistic (variable of interest): z
The p-value (variable of interest): \(p_{v}\)
Concepts and formulas used
In order to verify the assertion that the true proportion is greater than 0.28, we must test a hypothesis:
p ≤ 0.28 indicates a null hypothesis.
p > 0.28 is an alternative hypothesis.
The z statistic is required when doing a proportion test because it is provided by:
\(z= \frac{\bar p \;-\; p_{0}}{\sqrt{\frac{p_{0}\; (1\; - \; p_{0} ) }{n} } } \;\;\;\;\;\; ................ep.\; 1\)
Determine the statistic.
Since we have all the necessary information, we can change equation 1 to read as follows:
\(z= \frac{0.32 \;-\; 0.28}{\sqrt{\frac{0.28\; (1\; - \; 0.28) }{130} } } \;\;\;\;\;\; \\\\z = \frac{0.04}{\sqrt{\frac{0.28\; * \; 0.72 }{130} } } \\\\z = \frac{0.04}{\sqrt{\frac{0.2016 }{130} } }\\\\z = 1.01575 \;or\; 1.02\)
Statistical decision
The p-value for this test would then be calculated as the next step.
The p-value for this right-tailed test would be:
\(p_{v} = P \;(z > 1.02) = 0.1539\)
Since we are determining whether the mean is greater than a value, with z = 1.01575, the p-value is obtained using a z-distribution calculator with a right-tailed test, and it is 0.1539.
Visit the link below to learn more about Standard deviation:
brainly.com/question/17062923
#SPJ4
What is the weakest precondition for the following assignment statement: x = y * 2 10 { x > 20}
Answers
The weakest precondition for the assignment statement "x = y * 2" with the postcondition "{ x > 20}" is "y > 10".
The weakest precondition represents the minimum condition that needs to be satisfied before executing a given assignment statement, such that the desired postcondition will hold true after the execution. In this case, the assignment statement is "x = y * 2", and the postcondition is "{ x > 20}".
To determine the weakest precondition, we need to find the minimum condition that guarantees the postcondition. In other words, we need to identify the minimum value or constraint for the variables involved that ensures the resulting value of x will be greater than 20.
In the given scenario, multiplying y by 2 increases its value. To satisfy the postcondition that x should be greater than 20, we need to ensure that the result of the multiplication is greater than 20. Since the minimum value that satisfies this condition is y > 10, it becomes the weakest precondition for the assignment statement.
Therefore, the weakest precondition for the assignment statement "x = y * 2" with the postcondition "{ x > 20}" is "y > 10".
Learn more about conditions here:
https://brainly.com/question/32551068
#SPJ11
Radicals/Fractional Exponents on Integers

Answers
Answer:
b.....................
\(\sqrt[5]{5} \cdot \sqrt[5]{5^2} = 5^{1/5} \cdot 5^{2/5} = \boxed{5^{3/5}}\)
