WHATS THE VOLUME OF THIS SPHERE?!?!?

Given:

The figure of a right angle triangle with hypotenuse=19, leg=x and opposite angle is 40°.

To find:

The trigonometric function that is used to solve for x.

Solution:

In a right angle triangle,

\(\sin \theta=\dfrac{Perpendicular}{Hypotenuse}\)

In can be written as:

\(\sin \theta=\dfrac{Opposite}{Hypotenuse}\)

Using this ratio for the given triangle, we get

\(\sin 40^\circ =\dfrac{x}{19}\)

Therefore, the correct option is C.

For series (a), the series converges for |z| ≤ 1, and for series (b), the series converges for |z| ≤ 1.

For series (a), ∑_{1}^{∞} n!z^n, we can determine the values of z for which the series converges by using the ratio test. The ratio test states that if the limit of the absolute value of the ratio of consecutive terms is less than 1, then the series converges.

Using the ratio test, we have:

lim_{n}^{∞} |{(n+1)!z^{(n+1)} / (n!z^n)|

= lim_{n}^{∞} |(n+1)z} / (z^n)|

=lim_{n}^{∞} |(n+1) / {z^{(n-1)}}|

For the series to converge, we need this limit to be less than 1. Let's consider two cases:

1. If |z| > 1, then as n approaches infinity, the absolute value of the ratio |(n+1)/z^{(n-1)}| will tend towards infinity. Therefore, the series diverges.

2. If |z| ≤ 1, then as n approaches infinity, the absolute value of the ratio |(n+1)/z^{(n-1)}| will tend towards zero. Therefore, the series converges.

For series (b), ∑_{1}^{∞} n!z^n, we can use the ratio test in a similar way to determine the values of z for which the series converges.

Using the ratio test, we have:

lim_{n}^{∞} |{(n+1)!z^{(n+1)²} / (n!z^{n²})|

= lim_{n}^{∞} |{(n+1)z^{(2n+1)}} / (z^{n²})|

= lim_{n}^{∞} |{(n+1)z^{(2n-1)}} / {z^{n²}}|

Again, we consider two cases:

1. If |z| > 1, then as n approaches infinity, the absolute value of the ratio|{(n+1)!z^{(n+1)²} / (n!z^{n²})|  will tend towards infinity. Therefore, the series diverges.

2. If |z| ≤ 1, then as n approaches infinity, the absolute value of the ratio |{(n+1)z^{(2n-1)}} / {z^{n²}}| will tend towards zero. Therefore, the series converges.

In summary, for series (a), the series converges for |z| ≤ 1, and for series (b), the series converges for |z| ≤ 1.

Learn more about series from the given link:

https://brainly.com/question/31401033

#SPJ11

For series (a), the series converges for |z| ≤ 1, and for series (b), the series converges for |z| ≤ 1.

For series (a), \(\sum_{1}^{\infty} n!z^n\), we can determine the values of z for which the series converges by using the ratio test. The ratio test states that if the limit of the absolute value of the ratio of consecutive terms is less than 1, then the series converges.

Using the ratio test, we have:

\(\lim_{n \to \infty}| \frac {(n+1)!z^{(n+1)}}{(n!z^n)} |\)

\(= \lim_{n \to \infty} |\frac {(n+1)z}{(z^n)}|\)

\(= \lim_{n \to \infty} |\frac {(n+1)}{z^{(n-1)}}|\)

For the series to converge, we need this limit to be less than 1. Let's consider two cases:

1. If |z| > 1, then as n approaches infinity, the absolute value of the ratio \(|\frac{(n+1)}{z^{(n-1)}}|\) will tend towards infinity. Therefore, the series diverges.

2. If |z| ≤ 1, then as n approaches infinity, the absolute value of the ratio \(|\frac{(n+1)}{z^{(n-1)}}|\) will tend towards zero. Therefore, the series converges.

For series (b), \(\sum_{1}^{\infty} n!z^n\), we can use the ratio test in a similar way to determine the values of z for which the series converges.

Using the ratio test, we have:

\(\lim_{n \to \infty} |\frac{(n+1)!z^{(n+1)^2}}{(n!z^{n^2})}|\)

\(= \lim_{n \to \infty} |\frac{(n+1)z^{(2n+1)}}{(z^{n^2})}|\)

\(= \lim_{n \to \infty} |\frac{(n+1)z^{(2n-1)}}{z^{n^2}}|\)

Again, we consider two cases:

1. If |z| > 1, then as n approaches infinity, the absolute value of the ratio \(|\frac {(n+1)!z^{(n+1)^2}}{(n!z^{n^2})}|\)  will tend towards infinity. Therefore, the series diverges.

2. If |z| ≤ 1, then as n approaches infinity, the absolute value of the ratio \(|\frac{(n+1)z^{(2n-1)}}{z^{n^2}}|\) will tend towards zero. Therefore, the series converges.

In summary, for series (a), the series converges for |z| ≤ 1, and for series (b), the series converges for |z| ≤ 1.

Learn more about series from the given link:

brainly.com/question/31401033

#SPJ11

Answer:

the answer to your equation is (5,1) in point form or x=5,y=1 in equation form.

Step-by-step explanation:

Solve for the first variable in one of the equations, then substitute the result into the other equation. hope this helps. :)

Answer:

if it is a linear equation system

here is the answer : x=\(\frac{4908}{5}\) and y=\(\frac{929}{5}\)

Step-by-step explanation:

y₁ =  [1  -4  0  1] and y₂ = [5  1  -6  -1] is the orthogonal basis for w using Gram-Schmidt process.

Given,

The set;

x₁ = [1  -4  0  1]

x₂ = [7  -7  -6  1]

We have to produce the orthogonal basis for w using the Gram-Schmidt process;

Here,

y₁ = x₁ =  [1  -4  0  1]

Now,

Solve for y₂

y₂ = x₂ - [x₂y₁ / y₁y₁] y₁

That is,

y₂ = [7  -7  -6  1] - ( [7  -7  -6  1] [1  -4  0  1] / [1  -4  0  1] [1  -4  0  1] ) × [1  -4  0  1]

y₂ =  [7  -7  -6  1] - (7 + 28 - 0 + 1) / (1 + 16 + 0 + 1) × [1  -4  0  1]

y₂ = [7  -7  -6  1]  - 36/18 × [1  -4  0  1]

y₂ =  [7  -7  -6  1] - 2  × [1  -4  0  1]

y₂ =  [7  -7  -6  1] - [2  8  0  2]

y₂ = [5  1  -6  -1]

That is,

The orthogonal basis for w using Gram-Schmidt process is,

y₁ =  [1  -4  0  1] and y₂ = [5  1  -6  -1]

Learn more about Gram-Schmidt process here;

https://brainly.com/question/17132977

#SPJ4

Answer:16 a 8 9 c 9

Step-by-step explanation:

Answer:

D

Step-by-step explanation:

D is the correct answer, (-y, x)

Answer:

2. |-4| < |-8|

3. |-5| > 1

5. |-2| = |2|

Answer:

2,3,5 are correct

Step-by-step explanation:

i took the test

Answer:

hi

Step-by-step explanation:

hop it help

Market Size: Qualitative data, Nominal scale. Promotion: Qualitative data, Nominal scale. Week: Qualitative data, Ordinal scale.

a) The categorical qualitative variables from the ones listed above are as follows  :Market Size.

This variable represents the size of the customer base (small, medium, or large market).Promotion: Type represents which promotion the store ran (Promotion 1, 2, or 3. They ran three different promotions for a new product to see which one is more effective.).

b) The numerical (quantitative) variables from the ones listed above are as follows: Sales: (In Thousands) represents the number sales (in $1000) made in the specified week of December (Week).Age: Store represents the age of the store in years. Week: Number represents the week in which the promotion ran (Week 1, 2, 3, 4 - captured sales of new product over four weeks) c) Level of measurement for each variable is given as follows :Sales: Quantitative data, Ratio scale.Age: Quantitative data, Ratio scale.

To know more about Qualitative visit:

https://brainly.com/question/29004144

#SPJ11

Answer:

y = 19.5

Step-by-step explanation:

4y = 78

y = 19.5

Answer:

19.5

Step-by-step explanation:

PUT MY ANSWER THE BRAINLIEST PLEASEEEEEE

The answers to the questions based on the circle graph are given as follows.

a. The degrees for each part of the circle graph are approximately -

b. The percentage of people who chose each day is approximately -

c. The number of people who chose each day is approximately -

d. See the table attached.

To find the values for each part of the circle graph, we need to determine the value of x.

Given the information provided -

Monday = x°

Tuesday = 3/2x°

Wednesday = 90°

Thursday = 3x°

Friday = 2x°

a. To find the value of x, we can add up the angles of all the days in the circle graph -

x + (3/2)x + 90 + 3x + 2x = 360°

Simplify the equation -

Now  calculate the valuesfor each   protionof the circle graph -

b. The percentage of people who chose each day

c. Calculate the number of   people who chose each day,we can use the percentage values andmultiply them   by the total number of people surveyed (200).

d. Organizing the results in a table - See attached table.

Learn more about Circle Graph at:

https://brainly.com/question/24461724

#SPJ1

Full Question:

Although part of your question is missing, you might be referring to this full question:

See attached Image.

The shortest lifespan will last less than 2.5 years.

What is standard deviation?

The standard deviation is a statistic that expresses how much variance or dispersion there is in a group of numbers. While a high standard deviation suggests that the values are dispersed throughout a wider range, a low standard deviation suggests that the values tend to be close to the established mean.

First, we must utilize the conventional normal table to determine the value for z if 10% of the region (probability) to its left will be present. We can observe that about z = -1.282.

Now, we have to find the value of x, that corresponds to the value of z.

Since,

(x - μ) / σ = z

(x - 3.1) / 0.5 = -1.282

                 x = 2.459

Hence, the shortest lifespan will last less than 2.5 years.

To know more about the standard deviation, click on the link

https://brainly.com/question/475676

#SPJ4

The center of the ellipse is the midpoint between the two foci, which is ((7+1)/2, -1) = (4,-1). The distance from the center to each focus is 3, which is half the length of the major axis.

Therefore, the distance from the center to each vertex is sqrt(5), and the length of the minor axis is 2sqrt(5). Using the standard form of the equation of an ellipse with center at (h,k), major axis of length 2a, and minor axis of length 2b, we have:

(x - h)^2 / a^2 + (y - k)^2 / b^2 = 1

Plugging in the given information, we get:

(x - 4)^2 / 3^2 + (y + 1)^2 / (sqrt(5))^2 = 1

Simplifying, we get:

(x - 4)^2 / 9 + (y + 1)^2 / 5 = 1

Therefore, the equation of the ellipse is (x - 4)^2 / 9 + (y + 1)^2 / 5 = 1.

Learn more about ellipse here: brainly.com/question/29201705

#SPJ11

Answer:

I think its $1 every 4 oz

Step-by-step explanation:

Basing this off that 4 * 4 is 16

Answer:

None of the Above are correct

Answer:

(2x - 3)  cm

Step-by-step explanation:

Area of window = height × length

Given:

To find the length of the window, factor the expression for Area.

Factor  \(4x^2+2x-12\):

Find 2 two numbers that multiply to the product of the leading coefficient and the constant (4 × -12 = -48) and sum to the coefficient of the middle term (2):  -6 and 8

Rewrite the middle term as the sum of these 2 numbers:

\(\implies 4x^2-6x+8x-12\)

Factorize the first two terms and the last two terms separately:

\(\implies 2x(2x-3)+4(2x-3)\)

Factor out the common term (2x - 3):

\(\implies (2x+4)(2x-3)\)

Therefore, the length of the window is (2x - 3)  cm

(2x-3)cm

Answer:

Solution given:

height =2x+4

length=?

Area of window =(4x²+2x-12)cm²

we have

length*height =Area

length*(2x+4)=4x²+2x-12......(1)

Firstly let factorize 4x²+2x-12

taking common 2(2x²+x-6)

doing middle term factorization 2(2x²+4x-3x-6)

=2(2x(x+2)-3(x+2))

=2(x+2)(2x-3)

substituting it in equation 1

length*(2x+4)=2(x+2)(2x-3)

length*2(x+2)=2(x+2)(2x-3)

length =2x-3 cm

The length of window is (2x-3)cm

(a) A nonzero vector orthogonal to the plane through the points P, Q, and R is (9, -17, 35). (b) The area of triangle PQR is \(\sqrt\)(811) / 2.

(a) To determine a nonzero vector orthogonal to the plane through the points P, Q, and R, we can first find two vectors in the plane and then take their cross product. Taking vectors PQ and PR, we have:

PQ = Q - P = (5, 1, -2) - (-4, 0, 0) = (9, 1, -2)

PR = R - P = (6, 4, 1) - (-4, 0, 0) = (10, 4, 1)

Taking the cross product of PQ and PR, we have:

n = PQ x PR = (9, 1, -2) x (10, 4, 1)

Evaluating the cross product gives n = (9, -17, 35). Therefore, (9, -17, 35) is a nonzero vector orthogonal to the plane through points P, Q, and R.

(b) To determine the area of triangle PQR, we can use the magnitude of the cross product of vectors PQ and PR divided by 2. The magnitude of the cross product is given by:

|n| = \(\sqrt\)((9)^2 + (-17)^2 + (35)^2)

Evaluating the magnitude gives |n| = \(\sqrt\)(811).

The area of triangle PQR is then:

Area = |n| / 2 = \(\sqrt\)(811) / 2.

To know more about nonzero vector refer here:

https://brainly.com/question/32673773#

#SPJ11

When sand is poured in a single spot, it forms a cone where the ratio between the height and radius of the base h/r = 3. The height changes when the height is 30 cm, \(dh/dt = 3/πr² (dh/dt) = 3/π(10)² (dh/dt) = 0.0095491 (dh/dt)\)

The volume of a cone is \(V = 1/3πr²h.\)

Let's solve the problem.How to find the volume of the cone?We know that the volume of the cone is\(V = 1/3πr²h\)

Here, r = 10 cm,

h = 30 cm.

Therefore,\(V = 1/3π(10)²(30)\)

\(V = 3141.59 cm³\)

We know that the volume of the sand poured in a minute is 1 cm³.So, the height of the sand after t minutes is h(t).The volume of the sand poured in t minutes is 1t = t cm³.

Thus, the volume of sand in the cone after t minutes is V + t.

Now, we can write\(1/3πr²h(t) = V + t\)

Hence, \(h(t) = 3(V + t)/πr²h(t)\)

= \(3(V/πr² + t/πr²h(t))\)

= \(3h/πr² + 3t/πr²h(t)\)

Now, we can differentiate h(t) with respect to t to find the rate of change of the height of the sand.

Let's do it.

\(dh/dt = 3/πr² (dh/dt) = 3/π(10)² (dh/dt) = 0.0095491 (dh/dt)\)

To know more about height visit:

https://brainly.com/question/29131380

#SPJ11

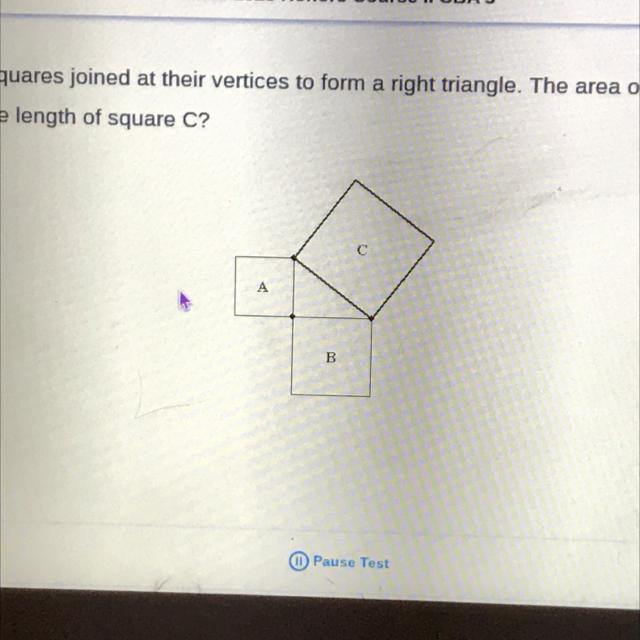
Answer:

side length of square C is 5 ft

Step-by-step explanation:

A, B andC are the areas of the sides of a right triangle.

C is the square on the hypotenuse of the right triangle.

using Pythagoras' identity in the right triangle.

the square on the hypotenuse is equal to the sum of the squares on the other 2 sides, that is

C² = A² + B² = 9 + 16 = 25 ft²

the area of a square is  s² , where s is the side length, then

s² = 25 ( take square root of both sides )

s = \(\sqrt{25}\) = 5 ft

Answer:

92.5%

Step-by-step explanation:

The ordered pair (1,-3) is a solution to the given system, while the ordered pair (0,0) is not

practice is a great way to help you understand how to determine whether ordered pairs are solutions to a given system. In this case, we are looking at the system:

3x+y=0

x+2y=-5

To determine whether the ordered pairs (0,0) and (1,-3) are solutions, we need to plug them into the equations and see if they make the equations true.

For the first ordered pair (0,0), we plug in x=0 and y=0 into the equations:

3(0)+(0)=0

(0)+2(0)=-5

The first equation is true, but the second equation is not. Therefore, (0,0) is not a solution to the system.

For the second ordered pair (1,-3), we plug in x=1 and y=-3 into the equations:

3(1)+(-3)=0

(1)+2(-3)=-5

Both equations are true, so (1,-3) is a solution to the system.

In conclusion, the ordered pair (1,-3) is a solution to the given system, while the ordered pair (0,0) is not.

Learn more about  ordered pairs

brainly.com/question/30113488

#SPJ11

The integral that gives the length of the curve f(x) = ln(cos(x)) is

\(\(\int_{0}^{\pi/3} \sec(x) dx\)\).

Arc length is the distance between two points along a section of a curve.

To find the length of the curve represented by the function f(x) = ln(cos(x)) from x = 0 to x = π/3, we can use the arc length formula for a curve given by y = f(x):

\(\[L = \int_{a}^{b} \sqrt{1 + \left(\frac{dy}{dx}\right)^2} dx\]\)

In this case, we need to find dy/dx first by differentiating f(x):

\(\(\frac{dy}{dx} = \frac{d}{dx} \ln(\cos(x))\)\)

Using the chain rule, we have:

dy/dx= - tan x

Now, substituting this value back into the arc length formula, we get the integral as:

\(\[L = \int_{0}^{\pi/3} \sqrt{1 + (-\tan(x))^2} dx\]\)

Simplifying the expression inside the square root:

\(\[L = \int_{0}^{\pi/3} \sqrt{1 + \tan^2(x)} dx\]\)

Using the trigonometric identity 1 + tan²(x) = sec²(x), we have:

\(\[L = \int_{0}^{\pi/3} \sqrt{\sec^2(x)} dx\]\)

Simplifying further:

\(\[L = \int_{0}^{\pi/3} \sec(x) dx\]\).

Learn more about integral:

https://brainly.com/question/30094386

#SPJ11

Answer:

x=27°

y=4 units

Step-by-step explanation:

To find x:

The sum of all the angles in a quadrilateral is 360°. In a rhombus (you know it's a rhombus because it's a quatrilateral where all the sides are congruent), opposite angles are congruent. Because you're given that the measure of ∠T is 127°, you also know that m∠V=127°. You also know that m∠U=m∠S=(2x-1)°.

Using this information, set up an equation.

127+127+(2x-1)+(2x-1)=360

You can just divide both sides by 2 to get:

127+(2x-1)=180

Then, just solve for x.

127+2x-1=180

2x+126=180

2x=54

x=27°

To find y:

All the sides are given to be congruent. That's what the little marks on the sides mean, and that's how we knew it was a rhombus earlier.

So SV=VU=UT=TS

SV=6y-5

VU=3y+7

Since SV=VU:

6y-5=3y+7

Solve for y.

3y=12

y=4

Hope I could help!

Answer:

Write out all the pairs of numbers which can be multiplied to produce c.

Add each pair of numbers to find a pair that produce b when added.

If b > 0, then the factored form of the trinomial is (x + d )(x + e).

Check: The binomials, when multiplied, should equal the original trinomial.

Answer: 8

Step-by-step explanation:

Fish cannot drown

Three died but they are still in the tank

The pieces of cake that Jeff will eat in 1 hour is 3

The pieces of cake that Gene will eat in 1 hour is 4

The pieces of cake that Mike will eat in 1 hour is 5

It will take Mike, Gene, and Jeff more than 1 hour to each eat the cake

In order to determine the pieces of cake that Jeff can eat in 1 hour, divide 6 by 2.

6/2 = 3 pieces of cake

In order to determine the pieces of cake that Gene can eat in 1 hour, multiply 2 pieces of cake by 2.

2 x 2 = 4 pieces of cake

In order to determine the pieces of cake that Gene can eat in 1 hour, multiply 4 pieces of cake by 60 minutes and divide the result by 48 minutes.

(4 x 60) / 48 = 5 pieces of cake

It will take Mike, Gene, and Jeff more than 1 hour to each eat the cake, because they all eat less than 8 slices of cake in one hour.

To learn more about division, please check: https://brainly.com/question/13281206

#SPJ1

To prove that a strictly increasing function from R to itself is one-to-one, we need to show that for any two distinct inputs in the domain, the function produces two distinct outputs in the range.

Let f be a strictly increasing function from R to itself, and let x, y be two distinct inputs in the domain of f, with x < y. Then, since f is strictly increasing, we know that f(x) < f(y), since x < y. This means that the outputs f(x) and f(y) are distinct, and therefore f is one-to-one.

To see why this is the case, suppose that f(x) = f(y) for some inputs x and y in the domain of f. Then, since f is strictly increasing, we know that x < y if f(x) < f(y), and x > y if f(x) > f(y). But if f(x) = f(y), then neither of these inequalities can hold, since they both require f(x) and f(y) to be distinct. Therefore, we have a contradiction, and it must be the case that f is one-to-one.

In summary, a strictly increasing function from R to itself is one-to-one because it produces distinct outputs for any two distinct inputs in the domain. This follows from the fact that if f(x) = f(y) for some x, y in the domain of f, then this would contradict the strict monotonicity of f.

To know more about increasing function visit:-

https://brainly.com/question/14330051

#SPJ11

Answer:

The property used is Symmetric property of Equality.

Option B is correct option.

Step-by-step explanation:

We are given :

\(AR \cong TY\\\)

Which property will give the step:

\(TY \cong AR\\\)

Looking at the options:

We see that Symmetric property states that if a = b then b= a

Same is the case with the question.

We have :

\(AR \cong TY\\\\TY \cong AR\\\)

If a = AR and b = TY

then the property is: a = b, b=a

So, the property used is Symmetric property of Equality.

Option B is correct option.

The limit definition of a derivative is a mathematical method used to calculate the instant rate of change of a characteristic at a particular point. it is based at the idea of the limit of a function because the input techniques a certain cost.

The limit definition of a derivative is expressed as follows:

\(f'(x) = lim (h → 0) [f(x + h) - f(x)] /h\)

Wherein f'(x) represents the derivative of the function f(x) at a particular factor x. The expression \(( f(x + h) - f(x)) / h\) represents the common price of alternate of the characteristic over a small interval of size h, focused at x. The limit of this expression as h approaches 0 represents the instant fee of change of the characteristic at x, or the slope of the tangent line to the function at that factor.

The limit definition of a derivative is a fundamental concept in calculus and is used to calculate the slopes of tangent lines, to find maximum and minimum factors, and to clear up optimization issues in a huge variety of packages.

Learn more about Limit definition of a derivative:-

https://brainly.com/question/30402318

#SPJ4