You buy 6 items for $25.60. About how much did you spend?
$125
$145
$75
$150
Answers
Answer: About $150.
Explanation: Each item cost $25.60, so I multiplied it into six, equalling about $150.
Related Questions
A simple random sample of 500 elements generates a sample proportion p= 0.81. Provide the 90% confidence interval for the population proportion (to 4 decimals). b.Provide 95% the confidence interval for the population proportion (to 4 decimals).
Answers
a) The 90% confidence interval for the population proportion is approximately (0.7777, 0.8423).
b) The 95% confidence interval for the population proportion is approximately (0.7737, 0.8463).
To calculate the confidence intervals for the population proportion, we can use the formula:
Confidence Interval = sample proportion ± margin of error
The margin of error can be calculated using the formula:
Margin of Error = critical value * standard error
where the critical value is determined based on the desired confidence level and the standard error is calculated as:
Standard Error = \(\sqrt{((p * (1 - p)) / n)}\)
Given that the sample proportion (p) is 0.81 and the sample size (n) is 500, we can calculate the confidence intervals.
a. 90% Confidence Interval:
To find the critical value for a 90% confidence interval, we need to determine the z-score associated with the desired confidence level. The z-score can be found using a standard normal distribution table or calculator. For a 90% confidence level, the critical value is approximately 1.645.
Margin of Error = \(1.645 * \sqrt{(0.81 * (1 - 0.81)) / 500)}\)
≈ 0.0323
Confidence Interval = 0.81 ± 0.0323
≈ (0.7777, 0.8423)
Therefore, the 90% confidence interval for the population proportion is approximately (0.7777, 0.8423).
b. 95% Confidence Interval:
For a 95% confidence level, the critical value is approximately 1.96.
Margin of Error = \(1.96 * \sqrt{(0.81 * (1 - 0.81)) / 500)}\)
≈ 0.0363
Confidence Interval = 0.81 ± 0.0363
≈ (0.7737, 0.8463)
Thus, the 95% confidence interval for the population proportion is approximately (0.7737, 0.8463).
Learn more about confidence interval here:
brainly.com/question/32546207
#SPJ4
the circumference of a circle is 18.84 in. What is the circle's diameter?
Answers
Answer:
6
Step-by-step explanation:
you do 18.84 and divide that by 3.14 and you will get 6 which is the diameter of the circle
Help me with this please

Answers
Answer: the answer is -5
Step-by-step explanation:
k
A pot contains 3 1/3 cups of oatmeal.
How many 3/5 cup servings is this? How much will be left
Answers
Answer:
2 11/15
Step-by-step explanation:
Hope this helps please mark brainliest if I helped! Thanks
Darnell can buy a particular brand of fruit juice in a 6-ounce bottle or a 10-ounce bottle. The juice in a 10-ounce bottle contains 150 calories. How many calories are in a 6-ounce bottle? Darnell can buy a particular brand of fruit juice in a 6-ounce bottle or a 10-ounce bottle. The juice in a 10-ounce bottle contains 150 calories. How many calories are in a 6-ounce bottle?
Answers
Answer:
a 6-ounce bottle or a 10-ounce bottle. The juice in a 10-ounce bottle contains 150 calories. How many calories are in a 6-ounce bottle? Darnell can buy a particular brand of fruit juice in a 6-ounce bottle or a 10-ounce bottle. The juice in a 10-ounce bottle contains 150 calories. How many calories are in a 6-ounce bottle?
Step-by-step explanation:
Darnell can buy a particular brand of fruit juice in a 6-ounce bottle or a 10-ounce bottle. The juice in a 10-ounce bottle contains 150 calories. How many calories are in a 6-ounce bottle? Darnell can buy a particular brand of fruit juice in a 6-ounce bottle or a 10-ounce bottle. The juice in a 10-ounce bottle contains 150 calories. How many calories are in a 6-ounce bottle?
-4(4x + 4) + 7(1 + 9x)
Answers
Answer:
47x - 9
Step-by-step explanation:
-4(4x + 4) + 7(1 + 9x)
-16x -16 + 7 + 63x
47x -9
You can find what x = because there is no = sign. This is in simplest form.
Answer:
47x -9
Step-by-step explanation:
\(-4(4x + 4) + 7(1 + 9x)\\\\\mathrm{Expand}\:-4\left(4x+4\right):\quad -16x-16\\=-16x-16+7\left(1+9x\right)\\\\\mathrm{Expand}\:7\left(1+9x\right):\quad 7+63x\\=-16x-16+7+63x\\\\\mathrm{Simplify}\:-16x-16+7+63x:\\\quad 47x-9\)
An urn contains n balls labelled 1 to n. Balls are drawn one at a time and then put back in the urn. Let M denote the number of draws before some ball is chosen more than once. Find the probability mass function of M. Hint for part (b): First find the distribution of M for a few small values of n and then try to identify the pattern for general n.
Answers
Let the probability mass function of the number of draws before some ball is chosen more than once be given by the function p(m;n).
SolutionFirst, let's consider the base case: $n = 2$Then the probability mass function is:p(1;2) = 0 (obviously)p(2;2) = 1 (after the second draw, the ball chosen must be the same as the first one)Now consider $n = 3$. We have two possibilities:either the ball drawn the second time is the same as the first one, which can be done in $1$ way, with probability $\frac{1}{3}$,or it isn't, in which case we need to draw a third ball, which must be the same as one of the first two.
This can be done in $2$ ways, with probability $\frac{2}{3} \cdot \frac{2}{3} = \frac{4}{9}$.Therefore:p(1;3) = 0p(2;3) = $\frac{1}{3}$p(3;3) = $\frac{4}{9}$Now we will prove that:p(m; n) = $\frac{n!}{n^{m}}{m-1\choose n-1}$.The proof uses the following counting argument. Suppose you have $m$ balls and $n$ labeled bins. The number of ways to throw the balls into the bins such that no bin is empty is ${m-1\choose n-1}$, and there are $n^{m}$ total ways to throw the balls into the bins.
Therefore the probability that you can throw $m$ balls into $n$ bins without leaving any empty bins is ${m-1\choose n-1}\frac{1}{n^{m-1}}$.For $m-1$ draws, we need to choose $n-1$ balls from $n$ balls, and then we need to choose which of these $n-1$ balls appears first (the remaining ball will necessarily appear second).
Hence the probability mass function is:$p(m; n) = \begin{cases} 0 & m \leq 1 \\ {n-1\choose n-1}\frac{1}{n^{m-1}} & m = 2 \\ {n-1\choose n-1}\frac{1}{n^{m-1}} + {n-1\choose n-2}\frac{n-1}{n^{m-1}} & m \geq 3 \end{cases}$We can simplify this by using the identity ${n-1\choose k-1} + {n-1\choose k} = {n\choose k}$. So we have:$p(m; n) = \begin{cases} 0 & m \leq 1 \\ {n\choose n}\frac{1}{n^{m-1}} & m = 2 \\ {n\choose n}\frac{1}{n^{m-1}} + {n\choose n-1}\frac{1}{n^{m-2}} & m \geq 3 \end{cases}$As required.
Learn more about Probability here,https://brainly.com/question/13604758
#SPJ11
What is the correct equation for the line in slope-intercept form?

Answers
Answer:
y = -5x + 35
Step-by-step explanation:
You have two points: (0, 35) and (7, 0).
The slope is \(\frac{0-35}{7-0}=-5\)
The y intercept is 35.
y = -5x + 35
Answer
Step-by-step explanat
What is the area please

Answers
The answer is 105 units²
Explanation:
Since the middle is a square, the base of all 4 triangles are equal.
Let x be the height of the triangles.
The height of the triangle can be defined as:
15 = 7 + x + x
15 = 7 + 2x
15 - 7 = 2x
x = 8/2
x = 4
Area = area of square + 4(area of triangle)
= (7 x 7) + 4(1/2(7)(4))
= 49 + 56
= 105 units²
I need help Please and thank you

Answers
Answer:
Brett baseball went higher
Step-by-step explanation:
his maximum is a vertical that exceeds 80
Albert claims that −6 is the greatest integer solution of the inequality 3x−1≤35+9x. Solve the inequality to show if Albert is correct or not.
Answers
Answer:
albert einstein
Step-by-step explanation:
Find the circumference.
Use 3.14 for it.
r = 4 cm
C = [?] cm
C=Td
![Find the circumference.Use 3.14 for it.r = 4 cmC = [?] cmC=Td](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/PfsQYBplGpEi6EOeJ7OVG9YPLFx9nH1j.png)
Answers
Answer:
25.12
Step-by-step explanation:
diameter is twice the radius. 4 times 2 = 8
3.14 times 8 = 25.12
(brainliest) asap help! D;

Answers
Answer:
3
Step-by-step explanation:
I will give you 40 points if you answer correctly
What is the distance of segment FG?

Answers
Answer:
dmfirnwudodnwbdovnwidovnwjchehqodnvnwocnfbwbxocjejajxkfek
12 13 & 14
please help. due soon

Answers
Answer:
(12) The perimeter of the four shaped figure is 12x - 10
(13) The perimeter of the rectangle is 18x + 10
(14) The perimeter of the hexagon is 24x
Step-by-step explanation:
(12) The perimeter of the four shaped figure is calculated as;
P = (x ) + (3x + 2) + (6x - 17) + (2x + 5)
Collect like terms together, in order to simplify the expression
P = (x + 3x + 6x + 2x) + (2 - 17 + 5)
P = 12x - 10
(13) The perimeter of the rectangle is calculated as;
P = 2( L + B)
P = 2L + 2B
Where;
L is length of the rectangle
B is the breadth of the rectangle
P = 2 (6x + 5) + 2(3x)
P = 12x + 10 + 6x
P = 18x + 10
(14) The perimeter of the hexagon is calculated as;
P = 6L
Where;
L is length of each side
P = 6 (4x)
P = 24x
PLSSS HELP IF YOU TURLY KNOW THISS

Answers
Answer: hii
1 4/6 Is the Answer I Believe.
Step-by-step explanation:
Hopefully this helps you
- Matthew
There are six bottles of juice for the same size and we need to make each kid have a 1/3 of a bottle how many kids will there be enough for is this the right story problem for 6÷1/3
Answers
Answer:
yes, 6÷1/3, which is 6×3 or 18
Step-by-step explanation:
A tv costs £800. Work out the price after a 3% discount.
Answers
3% = 800/ 100 = 8, 8x3= 24
800-24 = 776
£776
Answer:
Selling Price = £776
Step-by-step explanation:
Costing price = £800
Discount = 3% of 800
=> 3/100 × 800
=> 3×8
= £ 24
Selling Price = COSTING PRICE - DISCOUNT
Selling price = 800-24
Selling price = £776
Two divers are scuba diving. The first diver is 30 meters under water, which is 12 meters
deeper under water than the second diver. The second diver's depth, d, can be determined
using the equation d + 12 = 30. The gauge on the second diver's equipment says he is 16
meters under water. Is his gauge correct?
Answers
d=first diver depth
s=second diver depth
d= 30
S= 30-12=18
the equation given and the gauge must be wrong because the equation for the second duvet souls be s=d-12 since the first diver is DEEPER than the second.
tell me if the way I did it includes what's in this equation like if its commutative, associative, distributive or combined like terms

Answers
On the first line the distributive property was used. This property says that the product of a constant with a sum of two numbers is equal to the sum of the products.
On the third line the "associative" property was used. This property says that if you have the sum of three numbers the order at which you sum them doesn't affect the results.
HELP PLEASE What is the midpoint of the vertical line segment graphed below? (2,4) (2,-9)

Answers
Answer:
(2, -5/2)
Step-by-step explanation:
We can easily find the midpoint of this line using the midpoint formula. Although we can just find it by looking at the graph, let's try finding the midpoint using the formula to make sure we are correct.
\((\frac{x1+x2}{2}), (\frac{y1+y2}{2} )\)
\((\frac{2+2}{2}),(\frac{4+(-9)}{2})\\\\\\(\frac{4}{2}), (\frac{-5}{2})\\\\\\(2, \frac{-5}{2})\)
2y+y=5 what first step would need to be taken
Answers
Answer:
you would need to add the like terms together
Step-by-step explanation:
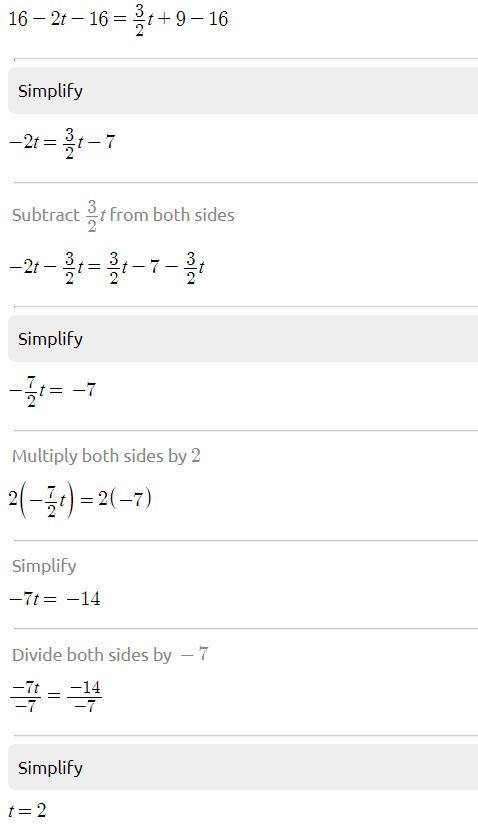
16−2t= 3/2t+9
need help asap this is my grade plz
kahn academy
plz help meee
Answers
Answer:
t=2
Step-by-step explanation:
I worked it out and got this answer as well but checked it in a calculator and couldn't send my pic in. I hope its right but if t is with 2 on the denominator then its a whole different answer.
A hiker begins at 2,000 feet above sea level and takes a break at 1,600feet above sea level. What is the hiker change in elevation?
Answers
Since they are both above sea level, all you would do is subtract
2000-1600=400
Explain the Error A student's solution to the equation 3x + 2 = 15
is shown. Describe and correct the error that the student made.
3x + 2 = 15
Divide both sides by 3.
x +2=5
Subtract 2 from both sides.
x=3

Answers
Answer:
3x+2=15
-2=-2
3x/3=13/3
_
x=4 1/3 = 4.33
Which linear equations have an infinite number of solutions? Check all that apply.
(x – 3\7) = 2\3 (3\2x – 9\14 )
8(x + 2) = 5x – 14
12.3x – 18 = 3(–6 + 4.1x)
1\2(6x + 10) = 7(3\7x – 2)
4.2x – 3.5 = 2.1 (5x + 8)
Answers
Answer:
a) (x – 3\7) = 2\3 (3\2x – 9\14 )
c) 12.3x – 18 = 3(–6 + 4.1x)
Step-by-step explanation:
A linear equation can be said to have an infinite number of solutions when the number of the right hand side is the same at the number on the left hand side of the equation.
For example:
2 = 2 or x = x or 0 = 0
Solving the question above:
Which linear equations have an infinite number of solutions? Check all that apply.
a) (x – 3\7) = 2\3 (3\2x – 9\14 )
x - 3/7 = 6x/6 - 18/42
x - 3/7 = x - 3/7
Collect like terms
x - x = -3/7 + 3/7
0 = 0
The linear equation in option a has an infinite number of solutions
b) 8(x + 2) = 5x – 14
8x + 16 = 5x - 14
Collect like terms
8x - 5x = -14 - 16
3x = -30
x = -30/3
x = -10.
The linear equation in Option b has a true solution.
c) 12.3x – 18 = 3(–6 + 4.1x)
12.3x - 18 = -18 + 12.3x
Collect like terms
12.3x - 12.3x = -18 + 18
0 = 0
The linear equation in Option c has infinite number of solutions
d) 1\2(6x + 10) = 7(3\7x – 2)
6x/2 + 5 = 21/7x - 14
3x + 5 = 3x - 14
Collect like terms
3x - 3x = -14 - 5
0 = -19
The linear equation Option d has no solution
e) 4.2x – 3.5 = 2.1 (5x + 8)
4.2x - 3.5 = 10.5x + 16.8
Collect like terms
4.2x - 10.5x = 16.8 + 3.5
-6.3x = 20.3
x = -20.3/6.3
x = -3.22
Hence, the linear equation in Option e has a true solution
Therefore, the linear equations have an infinite number of solutions are:
a) (x – 3\7) = 2\3 (3\2x – 9\14 )
c) 12.3x – 18 = 3(–6 + 4.1x)
Answer(x – 3\7) = 2\3 (3\2x – 9\14 ) and (12.3x – 18 = 3(–6 + 4.1x)
Step-by-step explanation:
there are 51 houses on a street. each house has an address between 1000 and 1099, inclusive. show that at least two houses have addresses that are consecutive integers.
Answers
according to the question,
given data in the question'
there are 51 houses on a street'
each hoses has an address between 1000 and 1099
There are 51 residences and 1000 possible addresses, according to the pigeon hole principle. There must be at least one address between each house in order for there to be no houses with consecutive addresses. To do this, only give houses even numbers (leaving odd addresses as the buffer address)
Giving houses even numbers (leaving odd addresses as the buffer address) There are now 1000=50 addresses that can be used.
According to the pigeon hole principle, there must be at least one box that contains at least N
k things if N objects are put into k boxes.
Because of this, it is impossible to assign 50 distinct addresses to 51 separate homes without utilising a single consecutive integer.
So, at least one instance of a home must have consecutive integers, which.
To know more about consecutive integers visit
https://brainly.com/question/12292611
#SPJ1
There are 2 houses that have at least consecutive integers .
What is meant by the pigeonhole principle?According to the pigeonhole principle, at least one container must hold more than one item if n things are placed into m containers, where n > m.
Why is pigeonhole principle important?According to the pigeonhole principle, if there are more pigeons than there are pigeonholes, then at least one pigeonhole must hold more than one pigeon. Although the underlying idea is clear, the ramifications are staggering. The explanation is that the principle establishes the reality (or absence) of a certain phenomena.
There are potential residences and addresses. There must be at least one address between each house in order for there to be no houses with consecutive addresses. To do this, only give houses even numbers (leaving odd addresses as the buffer address)
Houses are given even numbers, leaving odd addresses as the buffer address. As a result, we now have
50
addressable addresses
According to the "pigeon hole concept," if items are put into boxes, then there must be at least one box that contains at
[N/k]object.
As a result, it is impossible to assign distinct addresses to several dwellings without using at least one consecutive number.
Since there must be at least two homes with consecutive integer addresses, there must be at least one instance of consecutive integer addresses for houses.
To learn more about pigeonhole principle, click the following link:-
https://brainly.com/question/13982786
#SPJ4
Antonio has 150 baseball cards. He decided to give you 32% of his cards to you. How many cards did he give you?
Answers
Answer:
He gave you 48 cards.
Step-by-step explanation:
150 * 32% (which is also 0.32) is equal to 48.
Divide the percentage by 100.
32 / 100 = 0.32.
You then multiply 0.32 by 150 to get the part.
0.32 x 150 = 48.
32% of 150 is 48.
Your answer is 48 cards.
amal and ji both rent out their food trucks. the table shows the amounts amal and ji charge per hour to rent their food truck which statement is true
A- ji charges 75 per hour
B- amal charges 75 per hour
C- an equation that models amal’s fee is is y =50x+75
D - amal always charges 50 more than ji
Answers
Answer:
Step-by-step explanation:
americium-241 is widely used in smoke detectors. calculate the amount of americium-241 consumed in a smoke detector (initially containing 4.50 µg of am), in micrograms, that has been used for one year if the half-life is 433 years.
Answers
The amount of americium-241 consumed in a smoke detector, initially containing 4.50 µg, after one year can be calculated to be approximately 0.0104 µg.
The decay of americium-241 over time can be modeled using the radioactive decay formula:
A(t) = A₀ * (1/2)^(t / T₁/₂)
where:
A(t) is the amount of americium-241 remaining after time t,
A₀ is the initial amount of americium-241,
t is the time elapsed,
T₁/₂ is the half-life of americium-241.
In this case, the initial amount of americium-241 is 4.50 µg, and the half-life is 433 years. We want to calculate the amount remaining after one year.
Substituting the given values into the decay formula:
A(1 year) = 4.50 µg * (1/2)^(1 / 433)
Calculating this expression:
A(1 year) ≈ 4.50 µg * 0.998005
A(1 year) ≈ 4.492 µg
Therefore, the amount of americium-241 consumed in the smoke detector after one year is approximately 4.50 µg - 4.492 µg ≈ 0.0104 µg.
After one year, approximately 0.0104 µg of americium-241 would be consumed in a smoke detector initially containing 4.50 µg of americium-241, considering its half-life of 433 years.
To know more about amount, visit;
https://brainly.com/question/26574670
#SPJ11