Find the 3 smallest positive x-intercepts of the graph of
y = cos(12x) + cos(16x) and list them in increasing order.
Submit your answer as a list of x-coordinates from least to greatest.
Answers
To find the 3 smallest positive x-intercepts of the graph of y = cos(12x) + cos(16x), you can use the following steps:
Set y equal to 0 and solve for x to find the x-intercepts of the graph.
Since the graph of y = cos(12x) + cos(16x) is periodic with period 2π/12 = π/6 and 2π/16 = π/8, respectively, you only need to consider x-intercepts in the interval [0,π/6).
Use the identity cos(a+b) = cos(a)cos(b) - sin(a)sin(b) to rewrite the equation y = cos(12x) + cos(16x) as:
y = 2cos(4x)cos(8x) - sin(4x)sin(8x)
Set y equal to 0 and solve for x to find the x-intercepts. This will give you the x-coordinates of all the x-intercepts of the graph.
Sort the x-coordinates in increasing order and take the first three smallest positive values to find the 3 smallest positive x-intercepts.
For example, if you set y equal to 0 and solve for x, you get:
0 = 2cos(4x)cos(8x) - sin(4x)sin(8x)
This equation can be rewritten as:
cos(4x)cos(8x) = sin(4x)sin(8x)
Using the identity cos(a) = sin(π/2 - a) and substituting this into the equation above, we get:
sin(4x)sin(8x) = sin(4x + π/2)sin(8x)
This equation simplifies to:
sin(4x)sin(8x) = sin(4x)cos(8x)
Dividing both sides by sin(4x) and rearranging, we get:
sin(8x) = cos(8x)
This equation holds for all values of x that satisfy sin(8x) = cos(8x), so we can find the x-intercepts by setting these two functions equal to each other and solving for x:
sin(8x) = cos(8x)
sin^2(8x) = cos^2(8x)
sin^2(8x) - cos^2(8x) = 0
1 - cos(16x) = 0
cos(16x) = 1
Thus, the x-intercepts of the graph are at x = 0, x = π/16, x = π/8, x = 3π/16, and so on. Since we are only interested in the 3 smallest positive x-intercepts, we can take the first three values in this list: x = 0, x = π/16, and x = π/8.
Therefore, the 3 smallest positive x-intercepts of the graph of y = cos(12x) + cos(16x) are [0, π/16, π/8].
Related Questions
Joy is making a fruit salad. For every 2 cups of blueberries that Joy uses in the fruit salad, she uses 3 cups of strawberries. If Joy wants to use 6 cups of blueberries in the fruit salad, how many cups of strawberries will she need to use? Use Scratchpad to draw a tape diagram to show your work.
Answers
Answer:
Joy will need to use 9 cups of strawberries for 6 cups of blueberries.
Step-by-step explanation:
Given,
Cups of blueberries used for 3 cups of strawberry = 2
Ratio of cups of blueberry to strawberry = 2:3
Joy wants to use 6 cups of blueberries.
Let,
x be the cups of strawberry for 6 cups of blueberries.
Ratio of cups of blueberries to strawberries = 6:x
Using proportion;
Ratio of cups of blueberry to strawberry :: Ratio of cups of blueberries to strawberries
Product of extreme = Product of mean
Dividing both sides by 2
Given j(-8,-5) and l(6,-11) if k(r-4,2s) is the midpoint of jl which correctly gives the values of r and s?
Answers
The values of r and s is -1 and -4 respectively.
Given that:-
coordinates of j are (-8,-5)
coordinates of l are (6,-11)
coordinates of k are (r-4,2s)
Also, k is the mid-point of jl.
We have to find the values of r and s.
We know that, for (x,y) and (z,w), the mid-point is ((x+z)/2, (y+w)/2).
Here,
(x,y) = (-8.-5)
(z,w) = (6,-11)
(r-4,2s) = ((x+z)/2,(y+w)/2)
Hence,
(r-4,2s) = ((-8+6)/2,(-5-11)/2)
(r-4,2s) = (-1,-8)
Comparing the coordinates, we get:-
r - 4 = -1
r = -1+4 =3
2s = -8
s =-8/2 = -4
To learn more about mid-point, here:-
https://brainly.com/question/11302835
#SPJ4
48,000 is borrowed for 13 years. if the interest on the loan is 56,703.96, find the monthly payment
Answers
Answer:
130542
Step-by-step explanation:
FV=48000(2.7196)
FV=130542
Find x:
(Round the answer to the nearest tenth if there is a decimal)
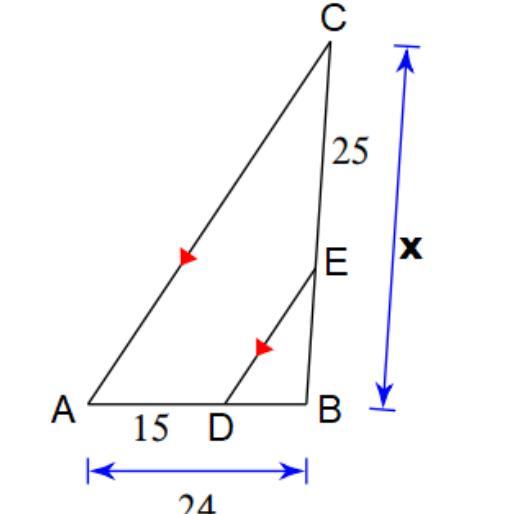
Answers
Answer:Angle x is congruent with the interior angle opposite side 8 (alternate interior angles)
Use tangent:
tan x = 8/15
x = arctan (8/15)
x = 28.1° (rounded)
Step-by-step explanation:
1. (1 point) Let x be a real number. Show that a (1 + x)2n > 1+ 2nx for every positive integer n.
Answers
For a real number x, by using mathematical induction it is shown that a\((1 + x)^{2n}\) > 1 + 2nx for every positive integer n.
To prove the inequality a\((1 + x)^{2n}\) > 1 + 2nx for every positive integer n, we will use mathematical induction.
The inequality holds true for n = 1, and we will assume it is true for some positive integer k.
We will then show that it holds for k + 1, which will complete the proof.
For n = 1, the inequality becomes a\((1 + x)^2\) > 1 + 2x.
This can be expanded as a(1 + 2x + \(x^2\)) > 1 + 2x, which simplifies to a + 2ax + a\(x^2\) > 1 + 2x.
Now, let's assume the inequality holds true for some positive integer k, i.e., a\((1 + x)^{2k}\) > 1 + 2kx.
We need to prove that it holds for k + 1, i.e., a\((1 + x)^{2(k+1)}\) > 1 + 2(k+1)x.
Using the assumption, we have a\((1 + x)^{2k}\) > 1 + 2kx.
Multiplying both sides by \((1 + x)^2\), we get a\((1 + x)^{2k+2}\) > (1 + 2kx)\((1 + x)^2\).
Expanding the right side, we have a\((1 + x)^{2k+2}\) > 1 + 2kx + 2x + 2k\(x^2\) + 2\(x^2\).
Simplifying further, we get a\((1 + x)^{2k+2}\) > 1 + 2(k+1)x + 2k\(x^2\) + 2\(x^2\).
Since k and x are positive, 2k\(x^2\) and 2\(x^2\) are positive as well.
Therefore, we can write a\((1 + x)^{2k+2}\) > 1 + 2(k+1)x + 2k\(x^2\) + 2\(x^2\) > 1 + 2(k+1)x.
This proves that if the inequality holds for some positive integer k, it also holds for k + 1.
Since it holds for n = 1, it holds for all positive integers n by mathematical induction.
Therefore, we have shown that a\((1 + x)^{2n}\) > 1 + 2nx for every positive integer n.
Learn more about mathematical induction here:
https://brainly.com/question/29503103
#SPJ11
determine whether descriptive or inferential statistics were used in the statement.
Answers
Without a specific statement provided, it is not possible to determine whether descriptive or inferential statistics were used. Please provide the statement in question for a more accurate analysis.
In order to determine whether descriptive or inferential statistics were used in a given statement, we need the specific statement or context. Descriptive statistics involves summarizing and describing data using measures such as mean, median, and standard deviation. It focuses on analyzing and presenting data in a meaningful and concise manner.
On the other hand, inferential statistics involves drawing conclusions and making inferences about a population based on sample data. It involves hypothesis testing, confidence intervals, and generalizing the results from the sample to the larger population. Without the statement or context, it is not possible to determine whether descriptive or inferential statistics were used.
Learn more about median here:
https://brainly.com/question/300591
#SPJ11
using a colored pencil, outline each triangle listed. which postulate proves these triangles are congruent?
Answers
SAS postulate is the postulate that proves the given triangles are congruent.
What is Triangle ?
Triangles are three-sided polygons with three vertices. The angles of the triangle are formed by connecting the three sides end to end at a point. The sum of the triangle's three angles equals 180 degrees.
Given,
A cube with congruent square faces.
Step 1: Create a labelled diagram by outlining the triangles and.
The diagram illustrating the triangles ΔABF and ΔBCG
See the attachment
Step 2 - Step description.
As an example, a cube has faces that are congruent squares.
Therefore, AB = BC = BF= CG and ΔABF = ΔBCG =90°
That implies, AB ≅ BC ≅ BF≅CG and ΔABF ≅ ΔBCG =90°
Step 3 - Description of step.
In the triangles ΔABF and ΔBCG, it can be seen that AB = BC , ΔABF =ΔBCG = 90° and BF=CG
Using the SAS postulate, the triangles ΔABF and ΔBCG are thus congruent triangles.
SAS postulate is the postulate that proves the given triangles are congruent
To learn more about Triangle visit:
brainly.com/question/29083884
#SPJ4

Cecelia planted 11 new flowers in her garden. The flowers were either yellow, which cost $1.60 each at the market, or purple, which cost $1.80 each. Cecelia paid a total of $18.20 when purchasing the flowers.
How many yellow flowers did Cecelia plant?
yellow flowers
PLEASE HELP ME
Answers
Answer:
8 yellow and 3 purple
Step-by-step explanation:

for the given point in polar coordinates, find the correspodning rectangular coordinates for the point (7, -pi/2)
Answers
The point (7, -π/2) in polar coordinates corresponds to the rectangular coordinates (0, -7), representing a point on the negative y-axis.
In polar coordinates, a point is represented by its distance from the origin (r) and its angle from the positive x-axis (θ). For the given point (7, -π/2), the distance from the origin is 7 units (r = 7), and the angle is -π/2 radians.
To convert this point to rectangular coordinates, we can use the following formulas:
x = r * cos(θ)
y = r * sin(θ)
Applying these formulas to the given values, we get:
x = 7 * cos(-π/2)
y = 7 * sin(-π/2)
The cosine of -π/2 is 0, and the sine of -π/2 is -1, so we can substitute these values into the formulas:
x = 7 * 0 = 0
y = 7 * (-1) = -7
Therefore, the rectangular coordinates for the point (7, -π/2) are (0, -7). This represents a point on the negative y-axis, where the x-coordinate is 0 and the y-coordinate is -7.
Learn more about cosine here: https://brainly.com/question/29114352
#SPJ11
I need help with this question

Answers
Answer:
A. \(\frac{3}{2}\)
General Formulas and Concepts:
Pre-Alg
Order of Operations: BPEMDASAlg I
Slope Formula: \(m=\frac{y_2-y_1}{x_2-x_1}\)Step-by-step explanation:
Step 1: Define
Point (-2, 1)
Point (2, -5)
Step 2: Find slope m
Substitute: \(m=\frac{-5-1}{2-(-2)}\)Simplify: \(m=\frac{-5-1}{2+2}\)Subtract/Add: \(m=\frac{-6}{4}\)Simplify: \(m=\frac{-3}{2}\)8w-2=12w+6 both answers
Answers
Answer:
your answer is -2
I hope it's helps you
Answer:
\(8w - 2 = 12w + 6 \\ 8w - 12w = 6 + 2 \\ - 4w = 8 \\ w = \frac{8}{ - 4} \\ w = - 2\)
I hope it helped U
stay safe stay happy
Jill is baking an apple pie. She cuts each apple into rectangular prism pieces and length 1 inch, width 1/4 inch, and height 1/2 inch. In total, she cuts 528 apple slices. What is the volume of each slice? What is the volume of all of the cut apples?
Answers
Step-by-step explanation:
Area of Rectangle Prism = Area of base x height
= Length x Width x Height
\( = 1 \times \frac{1}{4} \times \frac{1}{2} \\ = 0.125 {in}^{3} \)
One Apple Pie =
\(0.125 {in}^{3} \)
Volume of 528 Apple Pies = Volume of 1 apple pie x 528
=
\(0.125 \times 528 \\ = 66 {in}^{3} \)
HELP URGENTLY NEEDED STUCK ON THIS FOR 2 DAYS!!!!! LOTS OF POINTS FOR PERSON WHO HELPS!!!
Jada is three years older than twice her brother’s age. Select all the equations that correctly represent the relationship between Jada’s age j and her brother’s age b.
Multiple select question.
A) j=2b+3
B) j=2(b+3)
C) j=b2−3
D) b=2j+3
E) b=j−32
F) b=j2−3
Answers
Answer:
A
Step-by-step explanation:
2b meaning two times the age then add three like the question says.
Use the following two points to answer parts a -c . (2, 3) , (- 1, - 6) a. Find the slope of the line passing through the two pointsb . Write an equation of a line passing through the two points in point slope form . c . Rewrite the equation of the line in slope -intercept form .
Answers
sSlope means the inclination of the line
Intercept is the point where the line touches the Y axis.

If 18√8 - 8√18 = √n, what is n? Can you express 18√8 - 8√18 as multiples of the same square root?
Answers
Step-by-step explanation:
squaring both side
(18√8-8√18)^2=(√n)^2
(18√8)^2+(8√18)^2-(2)(8√18)(18√8)=n
after solving it we will get
3744-3456=n
n=288
=====================================================
Explanation:
Simplify the first part of the left side
\(18\sqrt{8} = 18\sqrt{4*2}\\\\18\sqrt{8} = 18\sqrt{4}*\sqrt{2}\\\\18\sqrt{8} = 18*2*\sqrt{2}\\\\18\sqrt{8} = 36\sqrt{2}\)
And do the same for the second part of the left side
\(8\sqrt{18} = 8\sqrt{9*2}\\\\8\sqrt{18} = 8\sqrt{9}*\sqrt{2}\\\\8\sqrt{18} = 8*3*\sqrt{2}\\\\8\sqrt{18} = 24\sqrt{2}\)
For each simplification, you are trying to factor the stuff under the square root so that you pull out the largest perfect square factor possible.
-------------------------
The original equation \(18\sqrt{8}-8\sqrt{18} = \sqrt{n}\) turns into \(36\sqrt{2}-24\sqrt{2} = \sqrt{n}\)
We have the common factor of \(\sqrt{2}\) so we can combine like terms on the left side ending up with \(12\sqrt{2}\)
-------------------------
So,
\(18\sqrt{8}-8\sqrt{18} = \sqrt{n}\\\\36\sqrt{2}-24\sqrt{2} = \sqrt{n}\\\\12\sqrt{2} = \sqrt{n}\\\\\sqrt{n} = 12\sqrt{2}\\\\\left(\sqrt{n}\right)^2 = \left(12\sqrt{2}\right)^2\\\\n = 288\)
Yes it is possible to express \(18\sqrt{8}-8\sqrt{18}\) as multiples of the same square root. In this case, we can express the left hand side of the original equation as 12 multiples of \(\sqrt{2}\)
A project under consideration has a 10-year projected life. The initial investment for the project is estimated to have a mean of $10,000 and a standard deviation of $1,000. The annual receipts are independent, with each year’s expected return having a mean of $1,800 and a standard deviation of $200. MARR is 12 percent. Assuming that initial investment and annual receipts are independent and normally distributed, estimate the probability that the present worth is negative using NORM.INV function in excel.
Answers
This value represents the present worth below which the probability is 0.5, indicating a negative present worth.
To estimate the probability that the present worth is negative using the NORM.INV function in Excel,
we need to calculate the present worth of the project and then determine the corresponding probability using the normal distribution.
The present worth of the project can be calculated by finding the sum of the present values of the annual receipts over the 10-year period, minus the initial investment. The present value of each annual receipt can be calculated by discounting it back to the present using the minimum attractive rate of return (MARR).
Using the given information, the present value of the initial investment is $10,000. The present value of each annual receipt is calculated by dividing the expected return of $1,800 by \((1+MARR)^t\),
where t is the year. We then sum up these present values for each year.
We can use the NORM.INV function in Excel to estimate the probability of a negative present worth. The function requires the probability value, mean, and standard deviation as inputs.
Since we have a mean and standard deviation for the present worth,
we can calculate the corresponding probability of a negative present worth using NORM.INV.
This value represents the present worth below which the probability is 0.5. By using the NORM.INV function,
we can estimate the probability that the present worth is negative based on the given data and assumptions.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ4
Which of the following statements contain a variable? Check all that apply
A. Half the height of the building.
B. She arrived at 2 o'clock.
C. There are 12 inches in a foot.
D. The length of the rope.
CO
Answers
Answer:
A., D.
Step-by-step explanation:
A. 0.5x
B. 2
C. 12
D. x
Answer: A., D.
The inequality below compares two rational numbers.
-2/3
<
-3/5
If the two number were plotted as values on a horizontal number line, which statement would be true?
Answers
We can conclude that -2/3 is indeed less than -3/5 when considering their positions on a horizontal number line.
To compare the rational numbers -2/3 and -3/5 on a horizontal number line, we can simplify them to decimal form.
The decimal equivalent of -2/3 is approximately -0.6667, and the decimal equivalent of -3/5 is approximately -0.6.
When we plot these values on a number line, we find that -0.6667 is to the left of -0.6.
Therefore, the statement "-2/3 < -3/5" is true when representing these numbers on a horizontal number line.
Visually, we can imagine the number line as follows:
-0.6667 -0.6
|-------------|
The left end, -0.6667, representing -2/3, is located to the left of the right end, -0.6, representing -3/5.
Thus, we can conclude that -2/3 is indeed less than -3/5 when considering their positions on a horizontal number line.
For similar question on rational numbers.
https://brainly.com/question/19079438
#SPJ11
-9 more than a number results in -20
Answers
Answer:
-9+x=-20
Step-by-step explanation:
I am not so positive on this one, but if you are not doing inequalities, then this should be correct.
"More than" would insinuate that you are adding. In this class, you would have a number to replace that x, but since no number was given, you place the x in its place. x=-11, because when you "add" -9 with something to get -20, it would have to be -11. Negative numbers can be confusing because when you subtract a negative number by another negative, you end up with a negative. Like in this case. Normally, you would just put -11, so it would look like -9 - 11 = -20. But since this says "more than", unless you are doing inequalities, you add.
If you are doing inequalities, then your answer should be this:
-9 > x = -20
I hope this helps!
-No one
two angles directly across from each other on intersecting lines Is called?
Answers
approximate the definite integral using the trapezoidal rule and simpson's rule. compare these results with the approximation of the integral using a graphing utility. (round your answers to four decimal places.) 3 1 ln(x) dx, n=4
Trapezoidal Simpson's Graphing Utility
Answers
From the graphing utility, we get the value of the integral as, Integral = 0.7206 Comparing the values of the integrals obtained from Trapezoidal rule, Simpson's rule and graphing utility, we find that the integral value obtained from the graphing utility is closest to the Simpson's rule.
We are given the definite integral ∫31ln(x)dx and we are required to approximate the integral using the trapezoidal rule and Simpson's rule. Also, we are supposed to compare these results with the approximation of the integral using a graphing utility using n=4.Trapezoidal Rule. The trapezoidal rule for numerical integration is a method to approximate the definite integral using linear interpolation.
This rule approximates the definite integral by dividing the total area into trapezoids. The formula for trapezoidal rule is given by:(Image attached)Here, a = 3 and b = 1The value of h can be calculated as follows;h=(b−a)/nh=(3−1)/4=0.5We need to calculate the values of f(1), f(1.5), f(2), f(2.5), f(3) using n = 4(Image attached)The value of integral using the trapezoidal rule is,Integral = 0.7201.
Simpson's rule is used to approximate the value of definite integral. Simpson's rule involves approximating the integral under the curve using the parabolic shape. This is done by dividing the area under the curve into small sections and then approximating each section with a parabolic shape. The formula for Simpson's rule is given as:(Image attached)Here, a = 3 and b = 1
The value of h can be calculated as follows;h=(b−a)/nh=(3−1)/4=0.5We need to calculate the values of f(1), f(1.5), f(2), f(2.5), f(3) using n = 4(Image attached)The value of integral using the Simpson's rule is,Integral = 0.7200Comparing with Graphing UtilityIntegral = 0.7201 (from Trapezoidal rule)Integral = 0.7200 (from Simpson's rule).
Learn more about Integral
brainly.com/question/18125359
#SPJ11
GIVING BRAINLIEST WHO WILL ANSWER FIRST
Which is equivalent to One-fourth x?
StartFraction 1 over 8 EndFraction x + StartFraction 1 over 8 EndFraction x
StartFraction 1 over 8 EndFraction x + StartFraction 1 over 8 EndFraction
StartFraction 1 over 8 EndFraction + StartFraction 1 over 8 EndFraction
One-half x + one-half x
Answers
Answer:
1/8x + 1/8x
Step-by-step explanation:
We are looking for 1/4x
1/8x + 1/8x = 2/8x which reduces to 1/4x
1/8x + 1/8 Cannot be added as they are not like terms
1/8 + 1/8 = 2/8 which reduces to 1/4 but doesn't have an x
1/2x + 1/2x = 2/2x which reduces to x
Therefore 1/8x + 1/8x is equivalent
Select the equation written in slope-intercept form that corresponds to the given slope and y-intercept. m=6 b=-2
Answers
Answer:
y = 6x - 2
Step-by-step explanation:
slope-intercept form: y = mx + b
Note that:
m = slope = 6
b = y-intercept = -2
x = (x , y)
y = (x , y)
Plug in the corresponding numbers to the corresponding variables:
y = 6x + (-2)
y = 6x - 2
y = 6x - 2 is your answer.
~
Answer:
y = 6x-2
Step-by-step explanation:
The slope intercept equation form of a line is
y = mx+b where m is the slope and b is the y intercept
y = 6x-2
Find the volume of the solid obtained by rotating the region in the first quadrant bounded by the curves x = 0, y = 1, x = y1°, about the line y = 1. 10
Answers
the volume of the solid obtained by rotating the region in the first quadrant about the line y = 1 is (4/3)π cubic units.
To find the volume of the solid obtained by rotating the region in the first quadrant bounded by the curves x = 0, y = 1, and x = y²2, about the line y = 1, we can use the method of cylindrical shells.
The volume of a solid of revolution can be calculated using the formula:
V = ∫(2πy)(h)dx
where y represents the height of each cylindrical shell, h represents the width of each cylindrical shell, and the integral is taken over the range of x-values that define the region.
In this case, the height of each cylindrical shell is given by y, and the width of each cylindrical shell is given by dx. The range of x-values is from 0 to 1, which corresponds to the curve x = y²2.
Therefore, we can set up the integral as follows:
V = ∫[from 0 to 1] (2πy)(dx)
To express y in terms of x, we solve the equation x = y²2 for y:
y = √x
Now we can rewrite the integral as:
V = ∫[from 0 to 1] (2π√x)(dx)
Integrating this expression will give us the volume of the solid:
V = 2π ∫[from 0 to 1] √x dx
To evaluate this integral, we can use the power rule for integration:
V = 2π ×[ (2/3)x²(3/2) ] evaluated from 0 to 1
Plugging in the limits of integration:
V = 2π ×[ (2/3)(1)²(3/2) - (2/3)(0)²(3/2) ]
Simplifying:
V = 2π ×(2/3)
V = (4/3)π
Therefore, the volume of the solid obtained by rotating the region in the first quadrant about the line y = 1 is (4/3)π cubic units.
To know more about Volume related question visit:
https://brainly.com/question/28058531
#SPJ11
Guided Practice Consider the following sequence. 3200,2560,2048,1638.4,dots Type your answer and then click or tap Done. What is the common ratio? Express your answer as a decimal.
Answers
If the sequence is 3200,2560,2048,1638.4,... then the common ratio of the sequence is 1.25.
To find the common ratio of the sequence, follow these steps:
The common ratio can be found by dividing each term in the sequence by its next term.So, 3200 ÷ 2560 = 1.25, 2560 ÷ 2048 = 1.25, 2048 ÷ 1638.4 = 1.25 and so on. So, it is found that the division of each term by its next term gives a constant value of 1.25. Hence, the common ratio of the given sequence is 1.25.Therefore, the common ratio of the sequence is 1.25
Learn more about sequence:
brainly.com/question/6561461
#SPJ11
Sara is saving her summer earning for a $500 school trip in the fall. She has $200 in her savings account at the beginning of June. Each week, Sara deposits $35 into her savings account. Sara wants to know how many weeks she needs to deposit her money?
Answers
500 = 200 + 35w
Subtract 200
300 = 35w, w = 8.57
Sara needs around 9 weeks
Need Help Giving 50 points

Answers
The answer is B
Hope this helps!
Consider u=x^2, v=1/u+1 and w=vy find dv/dx (3 marks) Thinking 9- Find the coordinates of the absolute maximum an d minimum points for f(x)=2x^2-x^4 given x €[0,4]
Answers
Consider the given, u=x²v
=1/u + 1w
=vy. The derivative of v with respect to x can be obtained by using the chain rule.
Here's how it can be done, dv/dx=dv/du × du/dx + dv/dx. By substituting the given values in the above formula, we get, dv/dx=dv/du × du/dx + dv/dy × dy/dx where, dv/du=-1/u²dv/dy
=v=1/u+1. Then, dv/dx
=dv/du × du/dx + dv/dy × dy/dx
= (-1/u²) × 2x + (1/(u+1)) × y Differentiating w.r.t x, we get, dw/dx
= dv/dx × y + v × dy/dx. Now, substituting the values of v, y, and dv/dx in the above equation we get,⇒ dw/dx = [(-1/u²) × 2x + (1/(u+1)) × (1/u+1)] × y + (1/u+1) × 2x. To find the maximum and minimum points for f(x)=2x²-x⁴, we need to first calculate its first derivative, f'(x) = 4x³ - 4x. Since we need to find the maximum and minimum points of f(x) in the range x € [0, 4], we set f'(x) equal to zero and solve for x. 4x³ - 4x = 0⇒ 4x(x² - 1)
= 0⇒ x
= 0, 1, or -1.
Since x € [0, 4], the values of x = 1 and
x = -1 can be ignored. We now need to evaluate the values of f(x) at
x = 0 and
x = 4 to determine the maximum and minimum points,
f(0) = 2(0)² - (0)⁴
= 0f(4) = 2(4)² - (4)⁴
= -32Therefore, the absolute maximum point is (4, -32) and the absolute minimum point is (0, 0).
To know more about derivative visit:-
https://brainly.com/question/29020856
#SPJ11
A caterpillar eats 1400%, percent of its birth mass in one day. The caterpillar's birth mass is m grams.
Which of the following expressions could represent the amount, in grams, the caterpillar eats in one day? (Choose 2 answers)
A) 140m B)1400m C)14m D)1400/100m E)1.4m
Answers
The expression that represents the amount in grams the caterpillar eats in one day is C) 14m
What is the percentage?A percentage is a value per hundredth. Percentages can be converted into decimals and fractions by dividing the percentage value by a hundred.
Let, The birth mass of the caterpillar be 'm'.
Given, It eats 1400%, percent of its birth mass in one day.
Therefore, The equation representing the amount, in grams, the caterpillar eats in one day is,
= (1400/100)×m.
= 14×m.
= 14m.
learn more about percentages here :
https://brainly.com/question/24159063
#SPJ1
At noon, ship a is 40 nautical miles due west of ship b. ship a is sailing west at 18 knots and ship b is sailing north at 17 knots. how fast (in knots) is the distance between the ships changing at 5 pm? (note: 1 knot is a speed of 1 nautical mile per hour.)
Answers
The distance between the ships changing at 92.29 Knots
Using the position of ship A as the reference point, at time t measured in hours past noon, ship A is 18 t miles west of this point and ship B is 40 + 17t north of this point. The distance between ships is then\(d(t) = \sqrt{(18t)^{2} + (40+17t)^{2} } \\\)
The rate of change of distance is -
\(\frac{dd}{dt} = \frac{36t + 2(40 + 17t)17}{2\sqrt{18t^{2} + (40 + 17t) } }\)
after putting t = 5 into this rate of change ,
we get, answer = 92.29
To learn more about differentiation from the given link
https://brainly.com/question/25081524
#SPJ4