Look at the image and answer please
Answers
Answer:
I would but there's no image
Related Questions
Solve for x: 3x - 5 = 2x + 6
Answers
Answer:
3x - 5 = 2x + 6
Step one- Subtract 2x to isolate the variable
X – 5 = 6
Step two- Add 5 to continue to isolate the variable
X = 11
Your answer is x = 11
Hopefully this helps! Feel free to mark brainliest!
Answer: x=11
Step-by-step explanation:
3x-5=2x+6
+5. +5
3x=2x+11
-2x -2x
x=11
If ∆JKL is an equilateral triangle, JK = 13x + 5, KL = 17x – 19, and JL = 8x + 35, what is the value of x?
Answers
Answer:
x = 6
Step-by-step explanation:
Given that Δ JKL is equilateral then the 3 sides are congruent.
Equate any 2 sides and solve for x, that is
13x + 5 = 8x + 35 ( subtract 8x from both sides )
5x + 5 = 35 ( subtract 5 from both sides )
5x = 30 ( divide both sides by 5 )
x = 6
An equilateral triangle is a triangle where all three sides are equal.
The value of x is 6.
What is a triangle?It is a two-dimensional figure which has three sides and the sum of the three angles is equal to 180 degrees.
We have,
An equilateral triangle is a triangle where all three sides are equal.
∆JKL is an equilateral triangle.
JK = 13x + 5
KL = 17x – 19
JL = 8x + 35
Now,
JK = 13x + 5
KL = 17x – 19
JK = KL
13x + 5 = 17x - 19
5 + 19 = 17x - 13x
24 = 4x
x = 6
Thus,
The value of x is 6.
Learn more about triangles here:
https://brainly.com/question/25950519
#SPJ2
A lamina occupies the region inside the circle x2 + y2 = 14y but outside the circle x2 + y2 = 49. Find the center of mass if the density at any point is inversely proportional to its distance from the origin.
Answers
The mathematical expression for the function that gives the center of mass is m=\(\(\int\limits \int\limits\)\(D_{p}\)(x, y)dA\)
What is center of mass?The center of mass is a point specified relative to an object or set of things. It is the weighted average position of all the system's pieces. For simple stiff objects with homogenous density, the centroid is the location of the center of mass.
A lamina that occupies the region inside the circle x²+y²=14y
Outside the circle is x²+y²=49.m
x²+y²=\(\(\int\limits\)P(x, y)dA\)
Where
r²=14rsinθ
x²+y²=49r=7
Therefore, the center of mass is-x=\((i/m) \(\int\limits\)xp(x, y)dA\)
-x=\((1/m)\(\int\limits \int\limits\)(r cosθ)p(r, θ)r drdθ\)
-y=\((1/m)\(\int\limits \int\limits\)Dyp(x, y)dA\)
-y= \((1/m)\(\int\limits \int\limits\)D(rsinθ)p(r, θ)r drdθ\)
Therefore, the center of mass is
m=\(\(\int\limits \int\limits\)\(D_{p}\)(x, y)dA\)
The mathematical expression for the function that gives the center of mass is
m=\(\(\int\limits \int\limits\)\(D_{p}\)(x, y)dA\)
To know more about functions, visit:
https://brainly.com/question/21011607
#SPJ4
Growth and decay how do you solve a(r)to the power of t

Answers
Solution for the question 2 :
It is given that ,
\(\begin{gathered} P_0=\text{ }800 \\ r\text{= }2\text{ \%} \\ n\text{ = 9 years} \end{gathered}\)The population after n years is given by exponential function ,
\(\begin{gathered} P(n)=P_0(1+\frac{r}{100})^n \\ \\ \\ \end{gathered}\)Population after 9 years is calculated as,
\(\begin{gathered} P(9)=\text{ 800 }\times(1+0.02)^9 \\ P(9)=\text{ 800 }\times(1.02)^9 \\ P(9)=800\text{ }\times\text{ 1.1951} \\ P(9)=\text{ }956.08\text{ }\approx\text{ 956 } \end{gathered}\)Thus the population after 9 years is 956 .
Help me to do exercise no 4
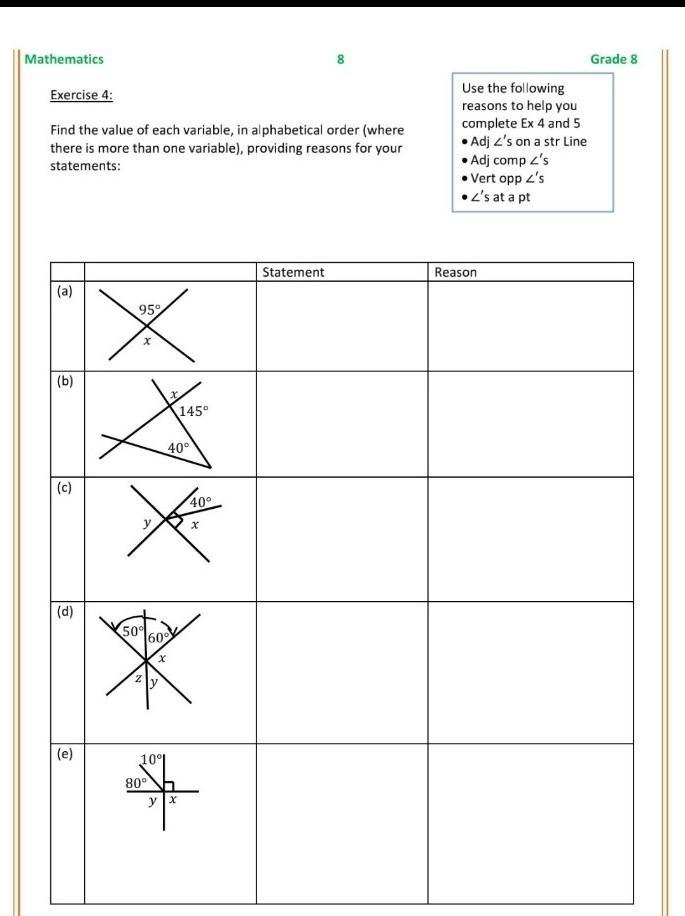
Answers
Answer:
y=50 and z=60 (vertically opposite)
x+60+y=180
or x+60+50=180
or x+110=180
or x=70
Answer:
Step-by-step explanation:
a.x = 95 degree
reason = being vertically opposite angles
x + 145 degree = 180 degree
x = 180 -145
x=35 degree
reason = being linear pair
b.40 + x =90 degree
x = 90 - 40
x = 50 degree
reason = being perpendicular
y = x + 40
y = 50 + 40
y = 90 degree
reason = being vertically opposite angles
c.50 + 60 + x=180 degree
110 + x =180
x = 180-110
x = 70 degree
reason = being linear pair
z = 60 degree
reason = being vertically opposite angles
y = 50 degree
reason = being vertically opposite angles
d. x = 80 +10
x =90 degree
reason = being vertically opposite angles
y + x =180 degree
y + 90 =180
y = 180 - 90
y = 90 degree
reason = being linear pair
The length of a given rectangle is six more than twice its width. Write a fully simplified expression to represent its perimeter.
Answers
Answer:
\(Perimeter = 12 + 6y\)
Step-by-step explanation:
Represent the length with x and width with y
By analysis, we have:
Length = 6 + 2 times the width.
Mathematically, the expression is:
\(x = 6 + 2 * y\)
\(x = 6 + 2 y\)
Required: Determine the perimeter
Perimeter of a rectangle is calculated as:
\(Perimeter = 2 * (Length + Width)\)
Substitute x for length and y for width
\(Perimeter = 2 * (x + y)\)
Substitute 6 + 2y for x
\(Perimeter = 2 * (6 + 2y + y)\)
\(Perimeter = 2 * (6 + 3y)\)
Open bracket
\(Perimeter = 2 * 6 + 2 * 3y\)
\(Perimeter = 12 + 6y\)
Simplify the expression:
3p+–p
Answers
Answer:
3p-p
Step-by-step explanation:
I always think of the negative sign out ruling the positive sign so let's do that for the -p part.
3p-p is what it becomes
Your question says simplify but just in case you want the answer here it is:
-p is also the same as -1p
So therefore we have
3p-1p
And we subtract the coefficients and keep the variable
2p would be your answer but once again I don't know if you wanted that so just to be sure I put 3p-p as my "answer".
In June, Clarissa used 1 gigabytes of data on her cell phone. Given that June has 30 days, how much data did she use on average per day?
Answers
Answer: 33.33 megabytes per day
Step-by-step explanation:
From the question, we are informed that in June, Clarissa used 1 gigabytes of data on her cell phone. Since June has 30 days, the amount of data she uses on average per day? will be:
= 1000megabyte/30
= 33.33mb
Note that:
1000 megabytes = 1 gigabyte
Select the correct answer from each drop-down menu.
Use the given functions represented by the equation and the graph to complete the statements.
f(x)=2x^3 - 3x^2 + 5x + 7
As x approaches positive infinity, f(x) approaches [negative infinity, positive infinity, zero] and g(x) approaches [negative infinity, positive infinity, zero]. The y-intercept of function f is [equal to, less than, greater than] the y-intercept of function g.

Answers
Answer:
f(x) approaches positive infinity.
g(x) approaches negative infinity.
the y-intercept of f(x) is less than the y-intercept of g(x).
Step-by-step explanation:
the highest power of x in f(x) is 3, and it has a positive sign. so, the bigger x the more the x³ part will dominate.
therefore, with x going to positive infinity, also f(x) goes to positive infinity.
the graph of g(x) clearly dives down never to come back up or flatten out. so, with x going to positive infinity, g(x) goes to negative infinity.
the y-intercept of f(x) = f(0).
that means the functional value when x=0.
so, for x=0 this means
y = 2×0³ - 3×0² + 5×0 + 7 = 7
the graph of g(x) shows that g(0) is 8.
so f(0) is less than g(0).
As x approaches positive infinity, f(x) approaches positive infinity and g(x) approaches negative infinity. The y-intercept of the function f is 7 and the y-intercept of function g is 8. #SPJ5
How to analyze the behavior of two given polynomialsPolynomials are algebraic expressions whose form is described below:
\(y = \sum \limits_{i = 0}^{n} c_{i}\cdot x^{i}\) (1)
Where \(c_{i}\) is the i-th coefficient of the polynomial.
In this question we have two polynomials in two distinct presentations, an analytical and a graphical one, whose behaviors must be analyzed to fill the blanks of the paragraph given. The complete paragraph is shown below:
As x approaches positive infinity, f(x) approaches positive infinity and g(x) approaches negative infinity. The y-intercept of the function f is 7 and the y-intercept of function g is 8. #SPJ5
To learn more on polynomials, we kindly invite to check this: https://brainly.com/question/20121808 #SPJ5
A 6-kg bowling ball sits on top of a building that is 120 meters tall.
Answers
The potential energy of the ball will be 7200 Joules.
What is potential energy?The energy possessed by a body by virtue of its position relative to others, stresses within itself, electric charge, and other factors.For small height changes, gravitational potential energy can be computed using - E = mgh.Given is a 6-kg bowling ball sits on top of a building that is 120 meters tall.
We can write the potential energy of the ball as -
E = mgh
E = 6 x 10 x 120
E = 60 x 120
E = 7200 Joules
Therefore, the potential energy of the ball will be 7200 Joules.
To solve more questions on potential energy, visit the link below -
https://brainly.com/question/24284560
#SPJ1
An object is translated by (x-2, y-6). If one point in the pre-image has the coordinates (-3, 7), what would be thecoordinates of its image?(-9,5)(-1, 13)(-5,1)(-1,7)
Answers
Answer:
C. (-5,1)
Explanation:
One point in the pre-image has the coordinates (-3, 7)
The translation rule is given below:
\((x,y)\to(x-2,y-6)\)Therefore, the coordinates of its image will be:
\(\begin{gathered} \mleft(-3,7\mright)\to\mleft(-3-2,7-6\mright) \\ =(-5,1) \end{gathered}\)The correct choice is C.
Evaluate the line integral, where C is the given curve. Integral C xyz ds, C: x=8 sin t, y=t, z=-8cos t, 0<=t<=pi
Answers
Hence, the required value of the line integral is\($\boxed{-84550}$\).
The given line integral is \($\int_{C}xyz ds$\), where the given curve C is \($x=8\sin t$, $y=t$, $z=-8\cos t$, $0\leq t\leq \pi$\).
Formula to evaluate line integral:\($$\int_{C}f(x,y,z)ds = \int_{a}^{b}f(x(t),y(t),z(t))\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2} dt$$Here, $f(x,y,z) = xyz$, $x(t)=8\sin t$, $y(t)=t$, $z(t)=-8\cos t$, $a=0$, $b=\pi$.\)
Hence, we have\($$\begin{aligned}\int_{C}xyz ds &= \int_{0}^{\pi} (8\sin t)(t)(-8\cos t)\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2+\left(\frac{dz}{dt}\right)^2} dt \\ &= \int_{0}^{\pi} (-64\sin t\cos t)(t)\sqrt{(8\cos t)^2+1^2+(-8\sin t)^2} dt \\ &= -64\int_{0}^{\pi} t\sin t\cos t\sqrt{64\cos^2t+64\sin^2t+1} dt\end{aligned}$$Let $u=64\cos^2t+64\sin^2t+1=65$, $du = 0$. When $t=0$, $u=65$, and when $t=\pi$, $u=65$\)
Hence, we have\($$\begin{aligned}& \int_{C}xyz ds = -64\int_{0}^{65} \left(\frac{t}{2}\right)\sqrt{u}\left(\frac{du}{32}\right) \\ &= -2\int_{0}^{65} t\sqrt{u}\ du \\ &= -2\left[\frac{2}{5}u^{\frac{5}{2}}\right]_{0}^{65} \\ &= -\frac{2}{5}(65)^{\frac{5}{2}} \\ &= -\frac{2}{5}(65)(65)^2 \\ &= \boxed{-84550}\end{aligned}$$\)
Learn more about integral
https://brainly.com/question/31433890
#SPJ11
1. Nasim thinks of a number.
When he multiplies his number by 5 and subtracts 16 from the result, he gets the same
answer as when ads 10 to his number and multiplies that result by 3.
Find the number Nasim is thinking of.
Answers
Step-by-step explanation:
5x-16 = 3 (10+x)
=> x= 23
12(5x + 10x²) = 256 + 60x
How do I solve this equation
Answers
Answer:
30
Step-by-step explanation:
idek

Question 1 (9 Points): a) Construct the second Taylor's polynomial P_{2}(x) for f(x)=\sin (2 x) , about x_{0}=0 . b) Use P_{2}\left(\frac{\pi}{3}\right) to approximate f\left("
Answers
The second Taylor polynomial of a function is a polynomial approximation to that function which is accurate near a particular point x0.
Construct the second Taylor's polynomial P2(x) for f(x)= sin(2x) about x0 = 0
We are to find the second Taylor polynomial for the function f(x) = sin (2x) about the point x0 = 0.
The second derivative of sin(2x) is -4 sin(2x),
so the second Taylor polynomial is given by:
P2(x) = f(x0) + f '(x0)(x - x0) + (1/2!)f ''(x0)(x - x0)²
P2(x) = sin(0) + cos(0)(x - 0) - 2sin(0)(x - 0)²
P2(x) = x - 2x²
Use P2(π/3) to approximate f(π/6)
We haveP2(x) = x - 2x²
Putting x = π/3, we get
P2(π/3) = (π/3) - 2(π/3)²
P2(π/3) = (π/3) - 2(π²/9)
P2(π/3) = (π/3) - (2π²/9)
To approximate f(π/6), we substitute π/6 for x in the original function. We get:
f(π/6) = sin(2(π/6))
= sin(π/3)
Now we use P2(π/3) to approximate sin(π/3):
sin(π/3) ≈ P2(π/3)
= (π/3) - (2π²/9)
≈ (1.05) - (2/3)(3.14)²
≈ 0.6724
We found that the second Taylor polynomial for the function f(x) = sin (2x) about the point x0 = 0 is:
P2(x) = f(x0) + f '(x0)(x - x0) + (1/2!)f ''(x0)(x - x0)²
P2(x) = sin(0) + cos(0)(x - 0) - 2sin(0)(x - 0)²
P2(x) = x - 2x²
We used P2(π/3) to approximate f(π/6) and found that sin(π/3) ≈ P2(π/3) = (π/3) - (2π²/9) ≈ 0.6724
The second Taylor polynomial of a function is a polynomial approximation to that function which is accurate near a particular point x0. The Taylor polynomial can be used to approximate function values near x0.
To know more about Taylor polynomial visit:
brainly.com/question/30481013
#SPJ11
HELP H>E>L>P help help

Answers
Answer:
i think b) option b
Step-by-step explanation:
lmk if this is incorrect
Find the difference ("subtract") between (x+7) & (3x+4)
Answers
After subtraction (3x+4) - (x+7), the resultant answer is 2x-3.
What is subtraction?One of the four operations used in mathematics, along with addition, multiplication, and division, is subtraction.
Removal of items from a collection is represented by the operation of subtraction.
For instance, in the following image, there are 5 2 peaches, which means that 5 peaches have had 2 removed, leaving a total of 3 peaches.
So, we have:
(x+7) and (3x+4)
We have to subtract as:
(3x+4) - (x+7)
Now, subtract as follows:
(3x+4) - (x+7)
3x+4 - x-7
2x-3
Therefore, after subtraction (3x+4) - (x+7), the resultant answer is 2x-3.
Know more about subtraction here:
https://brainly.com/question/13378503
#SPJ1
At the end of 1st Quarter of 2009 the median price of a single-family home in Charleston/No. Charleston was $184,990. Single-family home prices in Charleston/No. Charleston decreased from the 1st Qtr of 2008 by 8.15%. NOTE: Depreciation means a negative value for r. (a). Estimate the median price of a single-family home in the 1st Qtr of 2008.
(b). If the median price of a single-family home falls at the same rate for the next 2 years, estimate the median price of a single-family home in the 1st Qtr of 2011.
Answers
The estimated median price of a single-family home in Charleston/No. Charleston in the 1st Quarter of 2008 is $201,048. If the median price continues to decrease at the same rate for the next two years, the estimated median price of a single-family home in the 1st Quarter of 2011 would be $144,458.
(a) To estimate the median price of a single-family home in the 1st Quarter of 2008, we need to calculate the original price before the 8.15% decrease. Let's assume the original price was P. The price after the decrease can be calculated as P - 8.15% of P, which translates to P - (0.0815 * P) = P(1 - 0.0815). Given that the end of 1st Quarter of 2009 median price was $184,990, we can set up the equation as $184,990 = P(1 - 0.0815) and solve for P. This gives us P ≈ $201,048 as the estimated median price of a single-family home in the 1st Quarter of 2008.
(b) If the median price of a single-family home falls at the same rate for the next two years, we can calculate the price for the 1st Quarter of 2011 using the estimated median price from the 1st Quarter of 2009. Starting with the median price of $184,990, we need to apply an 8.15% decrease for two consecutive years. After the first year, the price would be $184,990 - (0.0815 * $184,990) = $169,805.95. Applying the same percentage decrease for the second year, the price would be $169,805.95 - (0.0815 * $169,805.95) = $156,012.32. Therefore, the estimated median price of a single-family home in the 1st Quarter of 2011 would be approximately $144,458.
To learn more about median click here: brainly.com/question/300591
#SPJ11
Jorge, sandra, danny, and valeria each mowed lawns after school and on the
weekends for a month. sandra mowed one-third of the number of lawns as jorge
and danny mowed half as many lawns as jorge. if valeria mowed 16 lawns and
the group mowed a total of 49 lawns in the month, how many did jorge mow?
Answers
Jorge mowed 18 lawns.
Let the number of lawns mowed by Jorge =x
So according to the question
Number of lawns mowed by sandra = x/3
Number of lawns mowed by Danny =x/2
Number of lawns mowed by Valeria =16
sum of total lawns mowed = lawns mowed by Jorge + lawns mowed by sandra + lawns mowed by Danny + lawns mowed by Valeria.
\(x+\frac{x}{3} +\frac{x}{2} +16=49\)
taking LCM as 6 and solving further we get
\(\frac{6x+2x+3x+96}{6} =49\)
By cross Multiplying we get
11x+96=294
11x=198
Solving further for x,
x=198/11
x=18
Therefore, the number of lawns mowed by Jorge is 18 .
Learn more about Ratio here https://brainly.com/question/15271657
#SPJ4
Help plz hhhhhhhhhh plz

Answers
What is an algebraic expression for this word phrase?
5 more than the product of 7 and n
5 + 7n
5(7+n)
7(5+n)
5 + 7 + n
Answers
1. Here are two expressions whose product is a new expression, A.
(5x++x³)(4x − 6) = A
Andre says that any real number can go in either of the boxes and A will be a
polynomial. Is he correct? Explain your reasoning
Answers
Yes, Andre is correct. That is any real number can go in either of the boxes will be a real number.
Polynomial expression:
Any expression which consists of variables, constants, and exponents, and is combined using mathematical operators like addition, subtraction, multiplication, and division in a polynomial expression.
The given polynomial expression is
(5 \(x^{4}\) + _x³ )( 4\(x^{ -}\) - 6) = A
Here in the blank space we can write any real number which will give a polynomial expression.
So, Andre is correct.
To know more about the polynomial expression refer to the link given below:
https://brainly.com/question/21865398
#SPJ9
There is a line that includes the point (18, -13) and has a slope of 0. What is its equation in
slope-intercept form?
Write your answer using integers, proper fractions, and improper fractions in simplest form.
Answers
Step by step
Slope of zero is a horizontal line since there is no rise and run
Point-slope form: y - y1 = m (x - x1)
y - - 13= 0(x - 18)
y + 13 = 0
y = -13
Slope-intercept form: y = - 13
How many times will the following loop execute?
int x = 0;
do {
x++;
cout << x << endl;
}while(x < 5)
Answers:
a. - 5 times
b. - 4 times
c. - It doesn't
d. - Infinite times
e. - 6 times
Answers
Answer:
Step-by-step explanation:
The loop will run an infinite number of times
help guys show your solution and answer the question

Answers
Answer:
Step-by-step explanation:
A)1) I found the LCM, by multiplying the common term with highest power and multiplying all the uncommon terms
2) I factored the trinomials into binomials that satisfies (i) the sum of two numbers is (-7) (ii) Product of the two numbers is 6
m=2/3; passes through the point (3,-1)
your response will be the number value for b
Answers
9514 1404 393
Answer:
-3
Step-by-step explanation:
The "b" is the y-intercept in the slope-intercept form ...
y = mx + b
Filling in the given values, we can find b.
-1 = (2/3)(3) +b
-1 = 2 + b . . . . simplify
-3 = b . . . . . . . subtract 2
The value for b is -3.

HELP, what’s the perimeter of the rectangle
Answers
Answer:
to find the perimeter of a rectangle , just add up all the values of the sides.
hope it helps :)
the taylor series for a fuction about x=0 is given by 2^k/3kx^k a) find f5(0) Show the work that leads to your answer.
Answers
The Taylor series for a function about x=0 is given by 2^k/3kx^k. We are supposed to find f5(0).The given Taylor series can be written as follows'(x) = ∑_k=0^∞▒(2^k)/(3k)x^k``f5(x) = (2^5)/(3×5)x^5``f5(0) = (2^5)/(3×5)×0^5 = 0`Therefore, f5(0) = 0. The work leading to this answer has been shown above.
To find f^(5)(0), we need to identify the term in the Taylor series that corresponds to the 5th derivative of the function evaluated at x=0. The general term in the Taylor series is given by:
(2^k / 3k) * x^k
We need to find the term where k = 5:
(2^5 / 3*5) * x^5 = (32 / 15) * x^5
Now, to find f^ (5)(0), we evaluate this term at x = 0:
(32 / 15) * 0^5 = 0
So, f^ (5)(0) = 0.
Learn more about Taylor series here:
https://brainly.com/question/12800011
#SPJ11
A person pulling a car with 2 children. A vector going from the ground to the person's hand is labeled 18 pounds. The vector horizontal to the ground is labeled 20 feet. The angle between the vectors is 20 feet.
It takes a constant force of 18 pounds applied at a 55° angle to pull a rolling cart 20 feet across the ground. What is the work done by the force?
Answers
The work done by the force can be found to be 206. 45 foot-pounds.
How to find the work done ?To find the work done by the force, the formula is:
Work = Force × Distance × cos (θ)
The angle was 55° , the distance was 20 feet and the force was 18 pounds. This is included in the question and so can be used to find the work done to be :
= 18 × 20 × cos ( 55 °)
= 18 × 20 × 0. 573576
= 206. 44568
= 206. 45 foot - pounds
In conclusion, the work done by the force was approximately 206. 45 foot - pounds.
Find out more on work done at https://brainly.com/question/31212311
#SPJ1
The work that is done by the force is 280.2 J.
What is work done?When a force acts on an object and causes it to move a specific distance, the amount of energy that is transmitted is known as the work done. It is described as the result of the amount of force that is exerted on an item and the distance that the object moves in the force's direction.
We have;
W = FdCosθ
W = work done
F = force
d = distance
θ = Angle turned
F = 18 Ib = 80.1 N
d = 20 feet = 6.1 m
θ = 55°
W = 80.1 N * 6.1 m * Cos 55
= 280.2 J
Learn more about work done:https://brainly.com/question/31655489
#SPJ1
purchased a total of 11 novels and magazines that have a combined selling price of $20, how many novels did she purchase?
Answers
The number of novels purchased was 9 novels.
Let the number of novels purchased be x and the number of magazines purchased be y.
Hence, \(x + y = 11.\)
Let the selling price of novels be a and that of magazines be b.
Therefore, \(ax + by = 20.\)
Similarly, given the price of magazines and novels as shown below:
\(a= 2\\b = 1\)
We can use the given equations above to find the number of novels purchased.
To find the value of x, we substitute the value of a and b into the equations,
\(ax + by = $20$2x + $1y \\= $20\)
We can also use the equation we found from \(x + y = 11,\) and solve for \(y:y = 11 - x\)
We can now substitute this value of y into the equation\(2x + 1y = 202x + 1(11 - x) \\= 201x \\=9x \\= 9 novels\)
Therefore, the number of novels purchased was 9 novels.
Know more about equations here:
https://brainly.com/question/17145398
#SPJ11