Please help!!!
3(x + 8) − 1 = 3x + 4
Answers
Answer:No value
Step-by-step explanation:there are no value solutions that make x a solution
Answer:
19
Step-by-step explanation:
3(x+8)-1=3x+3 3x+24-1=3x+4 3x+23=3x+4 3x+19=3x -3x+3x=19
x=19
Related Questions
J/-2 + 7 = -12 Please help guys!
Answers
Answer:
J=17
Step-by-step explanation:
J/-2 + 7 = -12
multiply both sides by -2 to cancel out the J/-2 and turn it into J + 7 = 24
transfer the 7 to the other side to get J = 24 - 7
J = 17
hopefully this helps.
Which set of measures could represent the length of the sides of a right triangle?
A) 2,3,4 B) 7,11,14 C) 8,10,12 D) 9,12,15
Answers
Answer:
B) 7,11,14
Step-by-step explanation:
correct me if I'm wrong
sketch the frist three vibrational eigenstates of a harmonic oscillator and use them to graphically determine whether the corresponding transition dipole matrix element is or is not equal to 0
Answers
To determine whether the transition dipole matrix element is equal to zero for the first three vibrational eigenstates of a harmonic oscillator, sketch the wavefunctions of these states and examine their symmetry properties.
The first three vibrational eigenstates of a harmonic oscillator are the ground state (n = 0) and the first and second excited states (n = 1, n = 2). These states have different spatial distributions and can be represented by wavefunctions.
By sketching the wavefunctions of these states, we can observe their shapes and examine their symmetry properties. If the wavefunctions exhibit an odd symmetry, it implies that the transition dipole matrix element is not equal to zero.
On the other hand, if the wavefunctions exhibit an even symmetry, it indicates that the transition dipole matrix element is equal to zero.
Based on the sketch of the first three vibrational eigenstates, we can determine whether the corresponding transition dipole matrix element is or is not equal to zero. The specific shapes and symmetry properties of the wavefunctions will provide visual evidence to make this determination.
Learn more about eigenstates here:
https://brainly.com/question/31317974
#SPJ11
The side lengths of a 45-45-90 triangles are in the ratio 1:1:square root 2. What is cos 45 degree ?
Answers
The cosine of 45 degrees is √2 / 2.
In a 45-45-90 triangle, the two legs are congruent and the hypotenuse is √2 times the length of each leg. The angles of a 45-45-90 triangle are 45 degrees, 45 degrees, and 90 degrees.
To find the cosine of 45 degrees, we can use the definition of cosine in a right triangle, which is defined as the ratio of the adjacent side to the hypotenuse. In a 45-45-90 triangle, the adjacent side and the hypotenuse are the same length.
Since the side lengths of a 45-45-90 triangle are in the ratio 1:1:√2, let's assume the length of one leg is x. Then, the length of the other leg is also x, and the length of the hypotenuse is √2x.
Now, let's consider the cosine of 45 degrees:
cos(45 degrees) = adjacent side / hypotenuse
= x / √2x
= 1 / √2
To simplify the expression, we can multiply both the numerator and the denominator by √2:
cos(45 degrees) = (1 / √2) * (√2 / √2)
= √2 / 2
for more questions on cosine
https://brainly.com/question/24305408
#SPJ8
pls if you can help

Answers
Answer:
x ≈ 8.4
Step-by-step explanation:
10
using the cosine ratio in the right triangle
cos64° = \(\frac{adjacent}{hypotenuse}\) = \(\frac{MN}{LN}\) = \(\frac{3.7}{X}\) ( multiply both sides by x )
x × cos64° = 3.7 ( divide both sides by cos64° )
x = \(\frac{3.7}{cos64}\) ≈ 8.4 ( to the nearest tenth )
ok so i have three questions 1. 4 – 3/7 = _______
2. 3/4 + 5/8 = _______
and 3. 1 – 4/5 = _______
Answers
4-3/7=
4*7/7-3/7=
28/7-3/7=25/7
Answer will be 3 4/7 or 25/7
Double the first one
3/4+5/8=
6/8+5/8=11/8
Answer will be 1 3/8 or 11/8
Same as the first
1-4/5=
1*5/5-4/5=
5/5-4/5=1/5
calculate the probability the proportion of the 30 americans sampled that agree climate change is an immediate threat to humanity exceeds 35%.
Answers
The probability that the proportion of the 30 Americans sampled that agree climate change is an immediate threat to humanity exceeds 35% is approximately 82.38%.
Assuming the sample of 30 Americans is representative of the population, we can calculate the sample proportion as the number of individuals in the sample who agree divided by the total sample size. Let's assume that the sample proportion is p'.
To calculate the probability of the proportion exceeding 35%, we need to find the z-score of the value 0.35 using the formula:
z = (p' - p) / √[p * (1 - p) / n]
where p is the population proportion (which we don't know), and n is the sample size (30 in this case). We can use p' as an estimate of p.
Once we find the z-score, we can use a standard normal distribution table or a calculator to find the probability that the z-score is greater than the value we calculated. This probability is the probability that the proportion of Americans who agree that climate change is an immediate threat to humanity exceeds 35%.
For example, if p' = 0.4, then the z-score is:
z = (0.4 - 0.35) /√ [0.35 * (1 - 0.35) / 30] = 1.03
Using a standard normal distribution table, we can find that the probability of a z-score being greater than 1.03 is approximately 0.8238, or about 82.38%.
To learn more about probability click on,
brainly.com/question/29035617
#SPJ4
(x divided by 3) - 6. it’s a divided by sign i just don’t have it. but written in a word phrase
Answers
Answer:
Step-by-step explanation:
- x over 3
Someone please help me asap! I will mark as brainliest, thank you!!

Answers
Answer:
Perimeter of ABCD = 2(24 + 26 + 28 + 25) = 206 mm.
Step-by-step explanation:
Perimeter of ABCD = 2(24 + 26 + 28 + 25) = 206 mm.
If the interest 4,000 for 4 years is 1,280 what is the interest rate
Answers
Answer:
For example, with a $4,000 deposit and an annual interest rate of 8 percent, the simple interest after four years would be $1,280. This is calculated by multiplying the principal (P) by the rate (R) and by the rate of time (T): 4,000 x 0.08 x 4 = 1,280.
Step-by-step explanation:
I hope the answer help you
CAN U PLEASE HELP!!!!

Answers
Answer:
C
Step-by-step explanation:
1/10 = 10/100
So 10/100 + 88/100 = 98/100
In a proof what is the reason that justifies this statement:
Segment BP is congruent to segment BP.

Answers
Answer: I believe that the BP segment is equal to BP segment because of the reflexive property.
Step-by-step explanation:
The required reason is that segment BP is congruent to segment BP that Segment BP is the common side among both triangles.
In congruent geometry, the shapes that are so identical. can be superimposed on themselves.
Here,
The necessary explanation is that segment BP and segment BP are congruent because segment BP is the common side of both triangles BPS and BPY, as shown in the figure.
Thus, the required reason is that segment BP is congruent to segment BP and that Segment BP is the common side among both triangles.
Learn more about congruent geometry here. https://brainly.com/question/12413243
#SPJ2
The question is in the png

Answers
Answer:
2 and 4 only
Step-by-step explanation:
hope it helped!!!
US
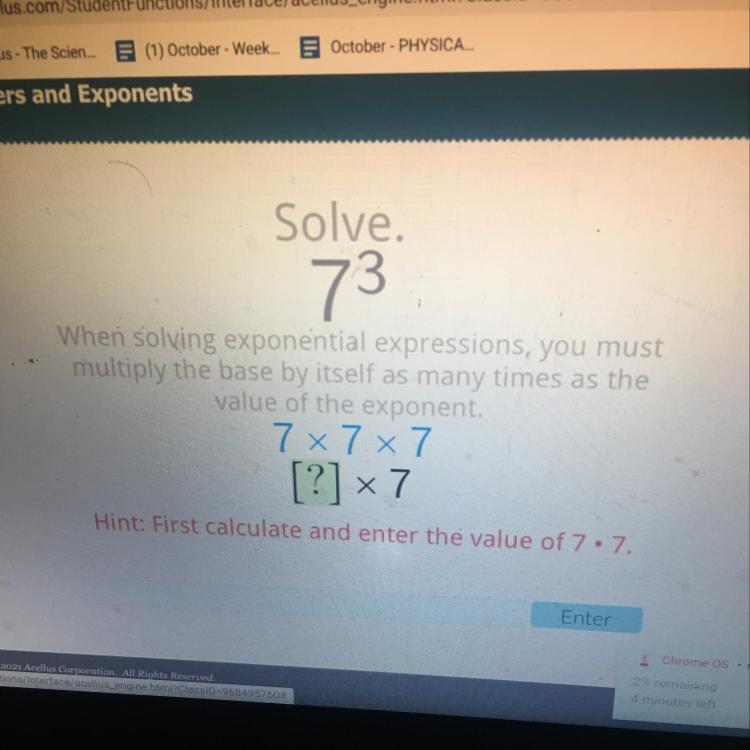
Solve.
73
When solving exponential expressions, you must
multiply the base by itself as many times as the
value of the exponent.
7x7x7
[?] x 7
Hint: First calculate and enter the value of 7.7.
M
Answers
\( {7}^{3} \\ = 7 \times 7 \times 7 \\ = 7^{1 + 1} \times 7 \\ = {7}^{2} \times 7 \\ = 49 \times 7\)
Answer:\(49\)
Hope it helps...ray4918 here to help
find a basis for and the dimension of the solution space of the homogeneous system of linear equations −x y z = 0 2x − y = 0 2x − 3y − 4z = 0 (a) a basis for the solution space
Answers
The homogeneous system of linear equations has a solution space with a basis of {(1, 2, -1)}. The dimension of the solution space is 1.
To find a basis for the solution space of the given homogeneous system of linear equations, we need to solve the system and express the solutions in terms of a linear combination of vectors.
The system of equations is as follows:
Equation 1: -x + y - z = 0
Equation 2: 2x - y = 0
Equation 3: 2x - 3y - 4z = 0
We can start by using the equations to eliminate variables. From Equation 2, we can express y in terms of x as y = 2x. Substituting this into Equation 1 gives us -x + 2x - z = 0, which simplifies to x - z = 0. Rearranging this equation, we have x = z.
Now, we can express the variables in terms of a single parameter. Let's choose z as the parameter. Thus, x = z and y = 2x = 2z.
Now, we can express the solutions in vector form as (x, y, z) = (z, 2z, z) = z(1, 2, 1). This means that the solution space is spanned by the vector (1, 2, 1).
To find the basis for the solution space, we need to check if the vector (1, 2, 1) is linearly independent. Since it is the only vector spanning the solution space, it is linearly independent. Therefore, the basis for the solution space is {(1, 2, 1)}.
The dimension of the solution space is equal to the number of vectors in the basis, which in this case is 1. Therefore, the dimension of the solution space is 1.
For more such questions on homogeneous, click on:
https://brainly.com/question/14778174
#SPJ8
If two angles are congruent, then they have the same measure.
Hypothesis:
Conclusion:
Answers
Hypothesis: If two angles are congruent.
Conclusion: Then they have the same measure.
The hypothesis states that if two angles are congruent, which means they are identical in shape and size, then the conclusion is that they have the same measure. In other words, when two angles are congruent, their measures are equal.
Angles are typically measured in degrees or radians. When we say that two angles are congruent, it implies that the measures of those angles are the same. This can be understood through the transitive property of congruence, which states that if two angles are congruent to a third angle, then they are congruent to each other.
For example, if angle A is congruent to angle B, and angle B is congruent to angle C, then it follows that angle A is congruent to angle C. This implies that the measures of angle A and angle C are equal, as congruent angles have the same measure.
In conclusion, the hypothesis that if two angles are congruent implies that they have the same measure is valid and supported by the principles of congruence and the transitive property.
For more information about hypothesis and conclusion, refer:
brainly.com/question/28564896
#SPJ11
solve for x and y pls and thank u

Answers
Answer:
fourth
Step-by-step explanation:
Angle X is the inscribed angle of the two arcs that measure 122 and 64 so
\(x = \frac{1}{2} (122 + 64)\)
\(x = \frac{1}{2} (186) = 93\)
A cyclic quadrilateral states that the opposite angles add up to 180
so
\(y = 18 0 - 83 = 97\)
The correct answer is the fourth option
HELP URGENT PLEASE HELPP

Answers
Answer:
x = √14Step-by-step explanation:
Let the common side of the triangles is s.
Use Pythagorean to get the value of s:
s² = 1² + 1² = 2and
s² = 4² - x² = 16 - x²Compare these equations and solve for x:
16 - x² = 2x² = 16 - 2x² = 14x = √14Help me with 1 and 2

Answers
Answer:
2)A function can be represented verbally. For example, the circumference of a square is four times one of its sides.A function can be represented algebraically. For example,3x+6.A function can be represented numerically.A function can be represented graphically.3)Comparing two mathematical functions and studying the properties of one function are two different problems. Most of the properties you listed are properties a function has, rather than what you would use to compare two functions. Yes you can compare two functions by stating that they have different domains/ranges, whether one is injective and another is not, but these comparisons aren’t really that interesting (rather, we are more interested in whether a function has certain properties).
Solve the equation to find x:7-3e^x=4
Answers
Explanation
\(\begin{gathered} 7-3e^x=4 \\ \end{gathered}\)to solve for x, isolate it
so
Step 1
\(\begin{gathered} 7-3e^x=4 \\ \text{subtract 7 in both sides} \\ 7-3e^x-7=4-7 \\ -3e^x=-3 \end{gathered}\)(-5 x 5x) - (-2 - 4)
Answers
There ya go hehehehhe

I need help immediately ASAP!!!!!!!! it's due today and I don't know what will happen to me. I'm dead

Answers
Answer:
C. y = 1/2x - 1
Step-by-step explanation:
The slope is 1/2 (line moves up 1 and right 2).
The y-intercept is -1 since that is where the line crosses the y-axis.
Please help and show workings!

Answers
Answer:
\(162\sqrt{3}\)
Step-by-step explanation:
The equation for finding the area of a hexagon with a side length is
\((s^23\sqrt{3} )/2\)
insert \(6\sqrt{3}\)
and you are left with 162\sqrt{3}
Hope that helps :)
Answer:
\( \displaystyle E)\: 162 \sqrt{3} \)
Step-by-step explanation:
we are given a side a polygon
and said to figure out the area
recall the formula of regular polygon
\( \displaystyle \: \frac{ {na}^{2} }{4} \cot \left( \frac{ {180}^{ \circ} }{n} \right) \)
where a represents the length of a side
and n represents the number of sides
the given shape has 6 sides
and has a length of \(\displaystyle 6\sqrt{3}\)
so our n is 6 and a is 6√3
substitute the value of n and a:
\( \displaystyle \: \frac{ {6 \cdot \:( 6 \sqrt{3} })^{2} }{4} \cot \left( \frac{ {180}^{ \circ} }{6} \right) \)
reduce fraction:
\( \displaystyle \: \frac{ {6 \cdot \:( 6 \sqrt{3} })^{2} }{4} \cot \left( \frac{ { \cancel{180}^{ \circ}} ^{ {30}^{ \circ} } }{ \cancel{6 \: } } \right) \)
\( \displaystyle \: \frac{6 \cdot \: (6 \sqrt{ {3} } {)}^{2} }{4} \cot( {30}^{ \circ} ) \)
simplify square:
\( \displaystyle \: \frac{6 \cdot \: 36 \cdot \: 3 }{4} \cot( {30}^{ \circ} ) \)
reduce fraction:
\( \displaystyle \: \frac{6 \cdot \: \cancel{36} \: ^{9} \cdot \: 3 }{ \cancel{ 4 \: } } \cot( {30}^{ \circ} ) \)
\( \displaystyle \: 6 \cdot \: 9 \cdot \: 3 \cot( {30}^{ \circ} ) \)
simplify multiplication:
\( \displaystyle \: 162\cot( {30}^{ \circ} ) \)
recall unit circle:
\( \displaystyle \: 162 \sqrt{3} \)
hence, our answer is E
AC is a diameter of OE, the area of the
circle is 289 units2, and AB = 16 units.
Find BC and mBC.
B
A
C
E. plssss hurry !!

Answers
The measure of arc BC is 720 times the measure of angle BAC.
Given that AC is the diameter of the circle and AB is a chord with a length of 16 units, we need to find BC (the length of the other chord) and mBC (the measure of angle BAC).
To find BC, we can use the property of chords in a circle. If two chords intersect within a circle, the products of their segments are equal. In this case, since AB = BC = 16 units, the product of their segments will be:
AB * BC = AC * CE
16 * BC = 2 * r * CE (AC is the diameter, so its length is twice the radius)
Since the area of the circle is given as 289 square units, we can find the radius (r) using the formula for the area of a circle:
Area = π * r^2
289 = π * r^2
r^2 = 289 / π
r = √(289 / π)
Now, we can substitute the known values into the equation for the product of the segments:
16 * BC = 2 * √(289 / π) * CEBC = (√(289 / π) * CE) / 8
To find mBC, we can use the properties of angles in a circle. The angle subtended by an arc at the center of a circle is double the angle subtended by the same arc at any point on the circumference. Since AC is a diameter, angle BAC is a right angle. Therefore, mBC will be half the measure of the arc BC.
mBC = 0.5 * m(arc BC)
To find the measure of the arc BC, we need to find its length. The length of an arc is determined by the ratio of the arc angle to the total angle of the circle (360 degrees). Since mBC is half the arc angle, we can write:
arc BC = (mBC / 0.5) * 360
arc BC = 720 * mBC
Therefore, the length of the arc BC equals 720 times the length of the angle BAC.
for such more question on measure of arc
https://brainly.com/question/25716982
#SPJ8
Can sum1 help please?

Answers
Answer: x=3
y=9
Step-by-step explanation: im about 75.94 percent sure about this, i hope it helps
Find the scale factor used to dilate quadrilateral LOVE, L (0,-7), O (5,-4), V (1,-5), E (3, -1) to L'O'V'E', L' (0, -21), O' (15, -12), V' (3, -15), E' (9,-3).
Answers
Answer:
7142213126 LOVE
Step-by-step explanation:
i dont no what i am doing this answer is wrong
In each of Problems 11 through 15, the coefficient matrix contains a parameter a. In each of these problems: a. Determine the eigenvalues in terms of a. b. Find the bifurcation value or values of a where the qualitative nature of the phase portrait for the system changes. 11. x' (-1a)x 5 3 13. x' alon | х a
Answers
11. a. Eigenvalues: \($\lambda = \alpha \pm i$\).
b. Bifurcation value: When \($\alpha$\) reaches a value where the eigenvalues become complex.
13. a. Eigenvalues: \($\lambda = \frac{5}{4} \pm \sqrt{\frac{3}{4}\alpha}$\).
b. Bifurcation value: \($\alpha < 0$\) where the eigenvalues transition from real to complex.
11. The given system is:
\(\[\mathbf{x}' = \begin{pmatrix}\alpha & 1 \\ -1 & \alpha\end{pmatrix}\mathbf{x}\]\)
a. To find the eigenvalues, we solve the characteristic equation:
\(\[\det(\mathbf{A} - \lambda \mathbf{I}) = 0\]\)
where \(\(\mathbf{A}\)\) is the coefficient matrix, \(\(\lambda\)\) is the eigenvalue, and \(\(\mathbf{I}\)\) is the identity matrix.
Substituting the values from the given system, we have:
\(\[\begin{vmatrix}\alpha - \lambda & 1 \\ -1 & \alpha - \lambda\end{vmatrix} = 0\]\)
Expanding the determinant, we get:
\(\[(\alpha - \lambda)^2 - (-1)(1) = 0\]\\\ (\alpha - \lambda)^2 + 1 = 0\]\)
Solving this quadratic equation, we find two complex eigenvalues:
\(\[\lambda = \alpha \pm i\]\)
b. The qualitative nature of the phase portrait changes when the eigenvalues have non-zero imaginary parts. In this case, it happens when \(\(\alpha\)\) reaches a bifurcation value such that the eigenvalues become complex. Therefore, the bifurcation value of \(\(\alpha\)\) is the one where the system transitions from real eigenvalues to complex eigenvalues.
13. The given system is:
\(\[\mathbf{x}' = \begin{pmatrix}\frac{5}{4} & \frac{3}{4} \\ \alpha & \frac{5}{4}\end{pmatrix}\mathbf{x}\]\)
a. Similar to problem 11, we solve the characteristic equation:
\(\[\begin{vmatrix}\frac{5}{4} - \lambda & \frac{3}{4} \\ \alpha & \frac{5}{4} - \lambda\end{vmatrix} = 0\]\)
Expanding the determinant, we get:
\(\[\left(\frac{5}{4} - \lambda\right)^2 - \left(\frac{3}{4}\right)(\alpha) = 0\]\)
\(\[\left(\frac{5}{4} - \lambda\right)^2 - \frac{3}{4}\alpha = 0\]\)
Simplifying and solving this quadratic equation, we find two eigenvalues in terms of \(\(\alpha\)\):
\(\[\lambda = \frac{5}{4} \pm \sqrt{\frac{3}{4}\alpha}\]\)
b. The qualitative nature of the phase portrait changes when the eigenvalues cross the imaginary axis. In this case, it happens when the discriminant of the quadratic equation becomes negative:
\(\[\frac{3}{4}\alpha < 0\]\)
Therefore, the bifurcation value of\(\(\alpha\)\) is \(\(\alpha < 0\)\) where the eigenvalues transition from real to complex.
The complete question must be:
In each of Problems 11 through 15 , the coefficient matrix contains a parameter \($\alpha$\). In each of these problems:
a. Determine the eigenvalues in terms of \($\alpha$\).
b. Find the bifurcation value or values of \($\alpha$\) where the qualitative nature of the phase portrait for the system changes.
11.\($\mathbf{x}^{\prime}=\left(\begin{array}{rr}\alpha & 1 \\ -1 & \alpha\end{array}\right) \mathbf{x}$\)
13. \($\mathbf{x}^{\prime}=\left(\begin{array}{cc}\frac{5}{4} & \frac{3}{4} \\ \alpha & \frac{5}{4}\end{array}\right) \mathbf{x}$\)
Learn more about eigenvalues:
https://brainly.com/question/30141989
#SPJ11
What is the range of the function on the graph?
-all the real numbers
-all the real numbers greater than or equal to 0
-all the real numbers greater than or equal to 2
-all the real numbers greater than or equal to -3

Answers
All the real numbers greater than or equal to -3,
Because when the line on the graph stops going downward and starts going upwards, or curves, it stops at -3, which means that all the number that are inside that line that are greater than it equal to -3, are going to be apart of the solution.
The range of the function on the graph is all the real numbers greater than or equal to -3.
What is Function?A function is a relation from a set A to a set B where the elements in set A only maps to one and only one image in set B. No elements in set A has more than one image in set B.
Range of a function is the set of all the output values of the function.
Here it is the set of all the y values for which the graph is defined.
The y values ranges from ∞ and comes down to -3 and again rises to
∞.
So the range is set of all the real numbers greater than or equal to -3.
Hence the correct option is D.
Learn more about Range here :
https://brainly.com/question/17440903
#SPJ7
PLEASE HELP ILL GIVE BRAINLIST

Answers
Answer:
B.
E.
Step-by-step explanation:
Answer:
A= 4.889
B= 5.06
C= 4.972
D= 4.992
E= 5.01
Step-by-step explanation:
YOUR WELCOMEEEE :>
Item 15 Your math class is collecting canned food for a local food drive. The goal is to collect at least 130 cans but no more than 250 cans due to space limitations. There are 24 students in your math class and your teacher has promised to bring in 10 cans. Select which inequalities represent the possible numbers $n$ of cans that each student should bring in.
Answers
For this case, the first thing we must do is define variables.
We have then:
n: number of cans that each student must bring
We know that:
The teacher will bring 5 cans
There are 20 students in the class
At least 105 cans must be brought, but no more than 205 cans
Therefore the inequation of the problem is given by:
Answer:
105 < 20n + 5 < 205
the possible numbers n of cans that each student should bring in is:
105 < 20n + 5 < 205