Answers
Answer:
32
Step-by-step explanation:
because 1 quart equals 4 cups so 8x4=32
Related Questions
Someone HELLPPPPPPPPPPPPP

Answers
Answer:
I am pretty sure the answer is B.
Answer:
B
Step-by-step explanation:
These are confusing, so I understand why it's a little bit of a frustration lol.
The first thing to look for is where the point is placed. This is -1, so make sure it's not on a positive 1.
All of them are using open circles, so this is such an easier way to tell which one to use. If it did have a closed and open circle for the point, remember that the inequality symbols > and < will always have an open circle. (By open I mean it isn't filled in).
The next thing to look for is to look where the line should be going. I can see that you selected D, but you want x to be less than -1, not greater. If the inequality symbol is turned away it means the number/variable is less than whatever it's being compared to, if that makes sense.
It's almost so simple yet so confusing at the same time. Good luck :)
I need
21
50
of fuel in %
Answers
Answer:
42%
Step-by-step explanation:
\(\frac{21}{50}\) as a percent
\(\frac{21}{50}=\frac{y}{100}\)
50 · y = 21 · 100
50y = 2100
50y ÷ 50 = 2100 ÷ 50
y = 42
the slope of a steep upward-sloping line will be a
Answers
Main Answer: The slope of a steep upward-sloping line will be a positive.
Supporting Question and Answer:
How is the slope of a line calculated?
The slope of a line is calculated by dividing the change in the y-coordinate (vertical change) between any two points on the line by the change in the x-coordinate(horizontal change)between the same two points.This is represented by the formula:
slope= \(\frac{(y_2-y_1)}{(x_2-x_1)}\) ,where \((x_1,y_1)\) and \((x_2,y_2)\) are two points on the line.
Body of the Solution:In mathematics, the slope of a line is defined as the ratio of the change in the y-coordinate to the change in the x-coordinate between any two points on the line. A positive slope indicates that the line is increasing in the y-direction as the x-coordinate increases.
A steep upward-sloping line means that the line is increasing rapidly in the y-direction as the x-coordinate increases, and therefore the slope of the line will be a large positive number. Conversely, a steep downward-sloping line will have a large negative slope, indicating that the line is decreasing rapidly in the y-direction as the x-coordinate increases.
Therefore, the slope of a steep upward-sloping line will be a positive.
Final Answer:The slope of a steep upward-sloping line will be a positive.
To learn more about the slope of a line from the given link
https://brainly.com/question/16949303
#SPJ4
What is the solution or solutions to the equation?
Answers
Solution of the equation is the collection of all values which are substituted for unknowns to cause an equation.
An assignment of values to the unknown variables that establishes the equality in the equation is referred to as a solution. To put it another way, a solution is a value or set of values (one for each unknown) that, when used to replace the unknowns, cause the equation to equal itself.
The solution is the set of all values that, when supplied as unknown replacements, cause an equation to hold true. The additive property and the multiplicative property are two fundamental algebraic rules that are used to find the solutions to equations requiring a single unknown raised to a power of one.
Learn more about Solution:
brainly.com/question/545403
#SPJ4
The front wheel of a bicycle has a radius of 20 in, and the back wheel has a radius of 15 in. How many revolutions does the small wheel make for every 30 revolutions of the big wheel
Answers
The number of revolutions the small wheel make for every 30 revolutions of the big wheel is 40.
What is equality of dimensional analysis?The fundamental idea behind dimension is that only quantities that have the same dimensions can be added or subtracted.
Similarly, only if two physical quantities have the same dimensions can they be equal.
Let r be the radius of the small wheel = 15 in.
Let R be the radius of large wheel = 20 in.
Let n be the number of revolution made by small wheel.
Let N be the number of revolutions made by large wheel = 30.
According to the equality of dimension,
rn = RN
15×n = 20 × 30
n = 40
Therefore, the total number of revolution made by small wheel for every 30 revolutions of large wheel is 40.
To know more about dimensional analysis, here
https://brainly.com/question/1769579
#SPJ4
At the Joseph Jacobs Exhibit at the museum, there is a Jack in the Beanstalk play place
with stairs and slide Jack's journey up the giant's lair. At the top of the stairs, there is a slide
to get down. Consider the diagram of the stairs and slide below.
If each step is two feet long and three feet high, then determine the angle of elevation
from the ground to the top of the stairs to the nearest tenth of a degree.
Answers
The angle of elevation from the ground to the top of the stairs is approximately 56.3 degrees to the nearest tenth of a degree.
In the given diagram, the vertical height of each step is 3 feet and the horizontal distance of each step is 2 feet.
Let h be the total vertical height from the ground to the top of the stairs. Then the number of steps, n, is given by:
h = 3n
The total horizontal distance, d, is given by:
d = 2n
We can use the Pythagorean theorem to relate the vertical height and horizontal distance to the angle of elevation, θ:
Beginning equation:
θ = h/d= 3n/2n = 3/2
Taking the arctan of both sides, we get:
θ = arctan(3/2) ≈ 56.3°
Therefore, the angle of elevation from the ground to the top of the stairs is approximately 56.3 degrees to the nearest tenth of a degree.
Find out more about angle of elevation
brainly.com/question/18882541
#SPJ4
To find the 95% confidence interval for the population standard deviation, you randomly sample with replacement from the original sample, thousands of times. From each new sample, you compute the sample standard deviation. Using the bootstrap method, how can you find the confidence interval for the population standard deviation from these values?.
Answers
Use 2.5th and 97.5th percentile of these values.
Bootstrapping, which is a type of test or metric that mimics the sampling process by using random sampling with replacement, belongs to the larger category of resampling techniques. With bootstrapping, sample estimates are given accuracy ratings such as bias, variance, confidence intervals, prediction error, etc.
A random sample with replacement from the original sample must be taken thousands of times in order to determine the 95% confidence interval for the population standard deviation. You calculate the sample standard deviation from each fresh sample.
From the values of the 2.5th and the 97.5th percentile of these data, we can use the bootstrap method to determine the 95% confidence interval for the population standard deviation.
So we need to use 2.5th and the 97.5th percentile of these values.
Learn more about percentile here:
brainly.com/question/2263719
#SPJ4
Graph f(x) = log base 3 x-1
Answers
Hello there. To solve this question, we have to remember how to graph a function.
First, remember that the logarithm in any base is an injective function (one-to-one).
We have to find its key-features before graphing it.
These key-features includes: x-intercept, y-intercept (if it exists), its vertical asymptote.
Okay. To find the x-intercept, set the function equal to zero:
\(f(x)=\log_3(x)-1=0\)Adding 1 on both sides, we get
\(\log_3(x)=1\)Apply the property:
\(\log_a(b)=c\Rightarrow b=a^c\)Hence we have
\(x=3^1=3\)So the x-intercept happens at x = 3.
To determine whether or not it has an y-intercept, we check if the limit as x goes to zero from both sides exists and are equal:
\(\begin{gathered} \lim_{x\to0^+}\log_3(x)-1=-\infty \\ \\ \lim_{x\to0^-}\log_3(x)=-\infty \end{gathered}\)In this case, this means we cannot evaluate this function at x = 0, so it doesn't have y-intercept(s).
Next, to determine its vertical asymptote, we check the value of x for which the argument goes to zero, that is
\(x=0\)Therefore it has a vertical asymptote at x = 0.
The graph is then given by:
This is a sketch of the graph of the function.
The final answer to this question is contained in the last option.

hello can you help me with this plane trigonometry question please and thank you for your time for doing this
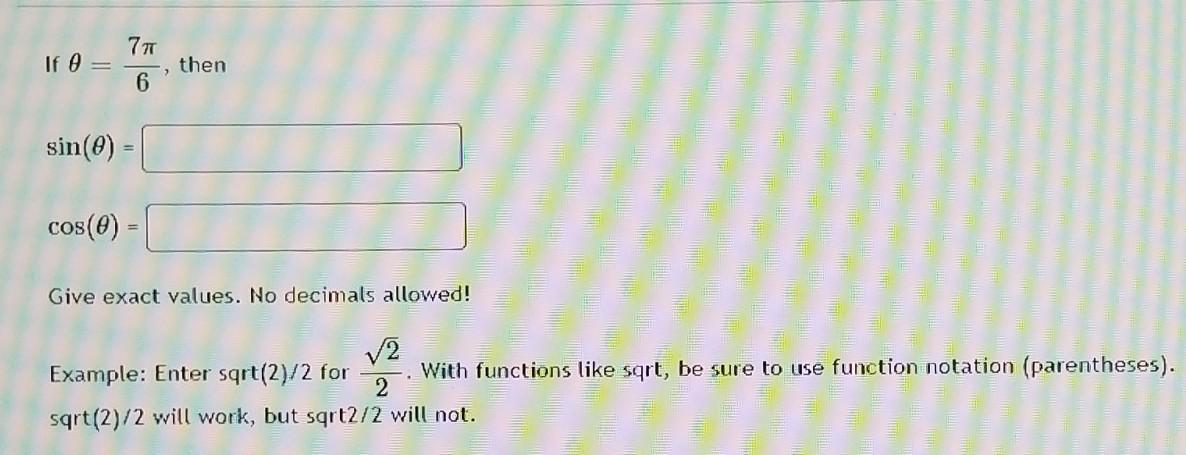
Answers
hello
\(\theta=\frac{7\pi}{6}\)\(\sin \theta=\frac{\sin 7\pi}{6}\)we need to first convert the values into degrees first
\(\begin{gathered} 2\pi=360 \\ \frac{7\pi}{6}=x \\ 2\pi x=\frac{7\pi}{6}\times360 \\ 2x\times6=7\times360 \\ 12x=2520 \\ x=\frac{2520}{12} \\ x=210 \\ \theta=210^0 \end{gathered}\)now we can convert the values in degrees to surds form
\(\begin{gathered} \sin 210=-\frac{1}{2} \\ \frac{\sin 7\pi}{6}=-\frac{1}{2} \end{gathered}\)now let's solve for cosine
\(\begin{gathered} \cos 210=-\frac{\sqrt[]{3}}{2} \\ \frac{\cos 7\pi}{6}=-\frac{\sqrt[]{3}}{2} \end{gathered}\)Xion baked 9 brownies for his friends. He wants to share them equally among his 4 friends so that everyone gets the same amount. If he wants to use all the brownies, how many brownies will each child get?
Answers
Answer:
(Excluding Xion) Each person will get 2 1/4 brownies
Step-by-step explanation:
9 brownies distributed equally to 4 friends. If each person gets two brownies, there is one left over. Divide 1 by 4 and you get 1/4. 1/4 in decimal form is 0.25. 2+0.25=2.25
Or you could just use a calculator to divide 9 by 4 and it would come up with 2.25
3500 dollars is placed in an account with an annual interest rate of 8.75%. to the nearest tenth of a year, how long will it take for the account value to reach 36700 dollars?
Answers
It will take approximately 4.3 years for the account value to reach $36,700 with an 8.75% annual interest rate.
1. Calculate the interest rate per period (year):
8.75%
= 0.0875
2. Calculate the number of periods (years) required to reach the desired total:
(36700-3500)/3500
= 10.2857
3. Calculate the final number of years to the nearest tenth of a year: 10.2857/0.0875
= 117.1429 or 4.3 years
To calculate the time it will take for the account value to reach $36,700, we need to first calculate the interest rate per period. In this case, the interest rate is 8.75% per year. This can be converted to a decimal by dividing 8.75 by 100 to get 0.0875. Next, we need to calculate the number of periods (years) required to reach the desired total. To do this, we subtract the initial account value of $3,500 from the desired account value of $36,700 and then divide this difference by the initial account value of $3,500. This gives us 10.2857. Finally, we need to calculate the final number of years to the nearest tenth of a year, which can be done by dividing 10.2857 by 0.0875. This gives us a result of 117.1429, which is equivalent to 4.3 years.
Learn more about rate here
https://brainly.com/question/13481529
#SPJ4
A runing track is 400m long. Carrie runs wight laps. How far is this in kilometres.
Answers
Multiply length of track by number of times run:
8 x 400 = 3,200 meters
1 km = 1000 meters
3200 meters / 1000 = 3.2 kilometers
Answer: 3.2 kilometers
Lesson 4-1 Solving Systems of Equations by Graphing
Answers
Answer:
Where's the question?
Step-by-step explanation:
Answer:
we cant answer it theres no backup to the question
Step-by-step explanation:
This function
Is it differentiable at x = 1 ?

Answers
It is not differentiable at x=1 since the slope of the tangent line as x -> 1 from the right is 1 while the slope of the tangent line as x->1 from the left is -1
By definition of absolute value:
\(|x - 1| = \begin{cases} x - 1 & \text{if } x \ge 1 \\ -(x-1) & \text{if } x < 1 \end{cases}\)
Then the derivative is
\(\dfrac{d|x-1|}{dx} = \begin{cases} 1 & \text{if } x > 1 \\ -1 & \text{if } x < 1\end{cases}\)
but does not exist at \(x=1\) because
\(\displaystyle \lim_{x\to1^-} f'(x) = -1\)
while
\(\displaystyle \lim_{x\to1^+} f'(x) = 1\)
and these limits are not equal, so the derivative is discontinuous and hence \(|x-1|\) is not differentiable at \(x=1\).
Find the point at which the line meets the plane X= 2+51 y=1 +21,2 = 2.4t x + y +z = 16 The point is (xy.z) (Type an ordered triple.)
Answers
The point at which the line defined by\(x = 2 + 51t, y = 1 + 21t\), and \(z = 2.4t\) meets the plane defined by\(x + y + z = 16\) is \((44, 22, -50)\).
To find the point of intersection, we need to equate the equations of line and the plane. By substituting the values of x, y, and z from the equation of the line into the equation of plane, we can solve for the parameter t.
Substituting \(x = 2 + 51t, y = 1 + 21t\), and \(z = 2.4t\) into the equation \(x + y + z = 16\), we have:
\((2 + 51t) + (1 + 21t) + (2.4t) = 16\)
Simplifying the equation, we get:
\(2 + 51t + 1 + 21t + 2.4t = 16\\74.4t + 3 = 16\\74.4t = 13\)
t ≈ 0.1757
Now that we have the value of t, we can substitute it back into the equations of the line to find the corresponding values of x, y, and z.
x = 2 + 51t ≈ 2 + 51(0.1757) ≈ 44
y = 1 + 21t ≈ 1 + 21(0.1757) ≈ 22
z = 2.4t ≈ 2.4(0.1757) ≈ -50
Therefore, the point at which the line intersects the plane is (44, 22, -50).
Learn more about equation of plane here:
https://brainly.com/question/32163454
#SPJ11
math, two questions I need help . look at the pic

Answers
Answeer
scan it with photo math it works
Step-by-step explanation:
Given points A(-1,4) and B(x,7), determine the value(s) of x if AB=5cm
Answers
The value of x is either 3 or -5 based on the distance formula.
What is a co-ordinate system?
In pure mathematics, a coordinate system could be a system that uses one or additional numbers, or coordinates, to uniquely confirm the position of the points or different geometric components on a manifold like euclidean space.
Main body:
according to question
Given points A(-1,4) and B(x,7)
Also AB = 5 cm
Formula of distance = \(\sqrt{(y1-y2)^{2}+(x1 -x2)^{2} }\)
here by using points ,
5 = \(\sqrt{(x+1)^{2} +(7-4)^{2} }\)
taking square on both side ,'
25 = \((x+1)^{2} +3^{2}\)
25-9 = (x+1)²
16 = (x+1)²
taking square root on both sides,
x+1= ±4
x = 4-1 = 3 or x = -4-1 = -5
Hence value of x is either 3 or -5.
To know more about point , visit:
https://brainly.com/question/26310043
#SPJ1
What is the answer step by step explanation please.
w (3w + 2) + 5w
Answers
Answer:8w^2+2
w(3w+2)+5w
First distribute the w to the parentheses:
3w^2+w
Add on the 5w to the new equation:
3w^2+2w+5w
Combine like terms:
8w^2+2
in grand haven, michigan the speed limit on mercury drive is 45 mph. residents with a driveway leading out to the road often complain that traffic tends to exceed 45 mph. during a two-week period, a traffic engineer installs a device that records the speed of each car that passes a certain point on mercury drive and flashes the speed to the driver. her goal is to get an idea of how fast cars travel on mercury drive. what is the variable being measured? residents with driveways leading out to the road the average speed of all cars the speed of each car the number of cars that drove faster than 45mph 1 points
Answers
The variable being measured is the speed of each car.
The variable being measured is the speed of each car since the traffic engineer is trying to get an idea of how fast cars travel on Mercury Drive. The speed is recorded and flashed to the driver in order to measure the speed of each car.
The traffic engineer is using a device to measure the speed of each car that passes a certain point on Mercury Drive. The device then flashes the speed to the driver, giving the traffic engineer an idea of how fast cars travel on the road. This allows for the variable of speed to be accurately measured and recorded, providing valuable data for the traffic engineer.
Learn more about variable here
https://brainly.com/question/29430246
#SPJ4
Find the sum of (3x + 2x ^ 3 - 5) + (- 4x + 3x ^ 3 - 8)
Answers
Answer:
-x + 5x^3 -13
Step-by-step explanation:
step 1: Collect like terms
3x - 4x + 2x^3 +3x^3 -5 - 8
step 2: simplify
5x^3 - x - 13
5x^3+3x-17
PLS HELP ............................

Answers
Answer:
The slope-intercept form is y = \(-\frac{3}{4}\) x + 8 ⇒ B
Step-by-step explanation:
The slope-intercept form of the linear equation is:
y = m x + b, where
m is the slopeb is the y-interceptFrom the given in the question
∵ The slope of the line is \(-\frac{3}{4}\)
∴ m = \(-\frac{3}{4}\)
→ Substitute its value in the form of the equation above
∴ y = \(-\frac{3}{4}\) x + b
→ To find b substitute x and y by the coordinates of any point on the line
∵ The line passes through the point (8, 2)
∴ x = 8 and y = 2
∵ 2 = \(-\frac{3}{4}\) (8) + b
∴ 2 = -6 + b
→ Add 6 to both sides to find b
∴ 2 + 6 = -6 + 6 + b
∴ 8 = b
→ Substitute the value of b in the equation above
∴ y = \(-\frac{3}{4}\) x + 8
∴ The slope-intercept form is y = \(-\frac{3}{4}\) x + 8
the sign for a new restaurant is an equilateral triangle with a height of 14 feet. what is the length of each side of the triangle, to the nearest tenth of a foot?
Answers
The length of each side of an equilateral triangle is equal to the square root of 3 times the length of its height. So, the length of each side of the sign is about 12.1 feet.
Here's the solution:
Let x be the length of each side of the triangle.
Since the triangle is equilateral, each angle is 60 degrees.
We can use the sine function to find the height of the triangle:
sin(60 degrees) = x/h
The sine of 60 degrees is sqrt(3)/2, so we have:
sqrt(3)/2 = x/h
h = x * sqrt(3)/2
We are given that h = 14 feet, so we can solve for x:
x = h * 2 / sqrt(3)
x = 14 feet * 2 / sqrt(3)
x = 12.1 feet (rounded to the nearest tenth)
Can someone please tell me what to put in question number 3 plz?

Answers
Answer:
It's 70, big man
Step-by-step explanation:
It's a forth of 280
HELPPPPPPPPPP PLS!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
18:16
You simplify
The teacher has listed 30 books as book report options. You must read 5. How many different sets of 5 books could you have chosen to read? (Stats question)
Answers
Answer:You can choose 6 different sets of 5 books to read.
Step-by-step explanation:All you need to do is do 30 divided by 5 and you get 6
Im pretty sure its permutation
30~5=6
Which of the following assumptions of linear regression is not also an assumption of analysis of
A. The random terms in the linear model are normally distributed.
B. The random terms in the linear model all have the same variance.
C. Both the independent variable and the dependent variable must be numeric.
D. The analysis is based on a random sample of data.
Answers
The assumption of linear regression that is not also an assumption of ANOVA is C. Both the independent variable and the dependent variable must be numeric.
The statistical technique known as Analysis of Variance or ANOVA is used to assess if there are significant differences between the means of two or more groups. Both the independent variables and the dependent variable are anticipated to be numerical in linear regression. Modelling the connection between numerical independent variables and a numerical dependent variable is the goal of linear regression.
However, in the concept of ANOVA, all independent variables are often numerical, but the dependent variable is typically categorical or group-based. ANOVA is used to compare averages across different groups and evaluate how category factors affect a numerical result.
Read more about ANOVA on:
https://brainly.com/question/25800044
#SPJ4
Chris has a six sided die. Create a sample
space of possible outcomes for rolling a number. Is this simple or compound event
Answers
Answer:
Sample space: {1, 2, 3, 4, 5, 6}
Simple event
Step-by-step explanation:
Sample space is a list of all the possible outcomes.
This is a simple event because you are only doing one event, such as rolling a die.
A compound event would be multiple simple events, such as flipping a coin and choosing a marble from a bag.
jules burns 100 kcalories during her morning walk. how many additional kcalories is she likely to burn in the post-exercise period?
Answers
15 additional kcalories is she likely to burn in the post-exercise period .
What do food calories mean?
When your body digests and absorbs food, calories are the amount of energy that is released. Foods that have more calories might give your body extra energy. Your body stores extra calories as body fat when you consume more calories than you need. Foods might contain a lot of calories even if they are fat-free.Since 1925, this calorie's definition has been based on the joule, and as of 1948, one calorie is roughly equal to 4.2 joules.jules burns 100 kcalories during her morning walk.
15 additional kcalories is she likely to burn in the post-exercise period .
Learn more about calories
brainly.com/question/22374134
#SPJ4
The width of bolts of fabric is normally distributed with mean 952 mm (millimeters) and standard deviation 10 mm. (a) What is the probability that a randomly chosen bolt has a width between 944 and 959 mm? (Round your answer to four decimal places.) (b) What is the appropriate value for C such that a randomly chosen bolt has a width less than C with probability 0.8438? (Round your answer to two decimal places.) C= You may need to use the appropriate appendix table or technology to answer this question
Answers
The width of bolts of fabric is normally distributed with mean 952 mm and standard deviation 10 mm. We need to find the probability that a randomly chosen bolt has a width between 944 and 959 mm.
Using z-score formula, we have;
z = (x - μ)/σ
where x is the given value, μ is the mean, and σ is the standard deviation.Now substituting the given values, we get;
z1 = (944 - 952)/10 = -0.8z2 = (959 - 952)/10 = 0.7
Using a standard normal table or calculator, we can find the probability associated with each z-score as follows:
For z1, P(z < -0.8) = 0.2119
For z2, P(z < 0.7) = 0.7580
Now, the probability that a randomly chosen bolt has a width between 944 and 959 mm can be calculated as;
P(944 < x < 959) = P(-0.8 < z < 0.7) = P(z < 0.7) - P(z < -0.8) = 0.7580 - 0.2119 = 0.5461:
The probability that a randomly chosen bolt has a width between 944 and 959 mm is 0.5461.
The probability that a randomly chosen bolt has a width between 944 and 959 mm was solved using the formula for z-score and standard normal distribution, where the probability associated with each z-score was found using a standard normal table or calculator. we are supposed to find the appropriate value for C such that a randomly chosen bolt has a width less than C with probability 0.8438.
To know more about z-score visit:
brainly.com/question/31871890
#SPJ11
Solve: 2.3 = v + 0.47 v = _____
Answers
Answer:
2.3=v+0.47v=
We move all terms to the left:
2.3-(v+0.47v)=0
We add all the numbers together, and all the variables
-(+1.47v)+2.3=0
We get rid of parentheses
-1.47v+2.3=0
We move all terms containing v to the left, all other terms to the right
-1.47v=-2.3
v=-2.3/-1.47
v=1+0.83/1.47
Answer:
\(v = 1.564\)
Step-by-step explanation:
\(1v + 0.47v = 2.3\)
\( = > 1.47v = 2.3\)
\( = > v = \frac{2.3}{1.47} = 1.564\)
