Answers
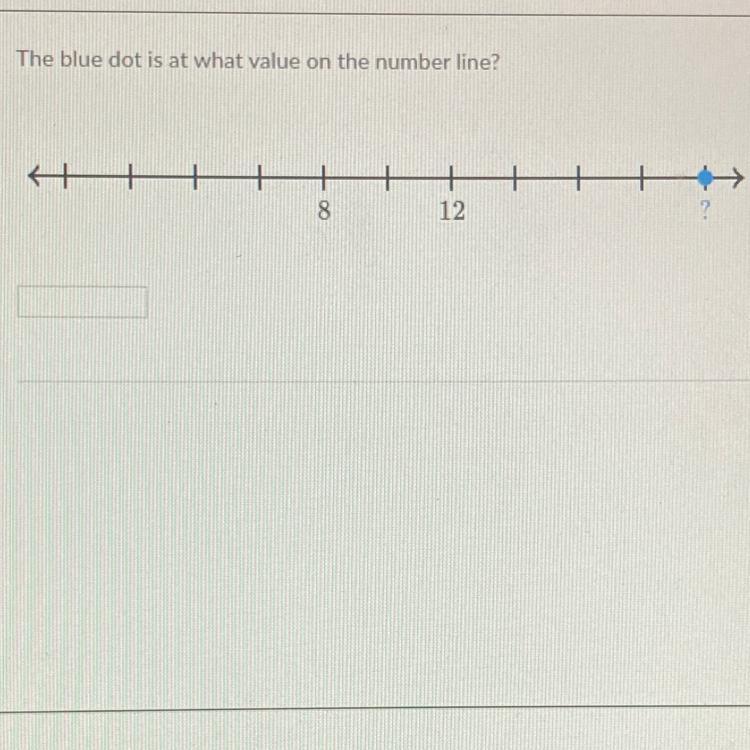
Answer:
20
Step-by-step explanation:
Your going by 2's
Answer:
20
Step-by-step explanation:
The graph is going up by 2 so add two every time to get 20
Related Questions
if the ratio of two sample variances exceeds the critical value of f at a defined confidence level, then___
Answers
if the ratio of two sample variances exceeds the critical value of f at a defined confidence level, then the level of confidence also exceeds the critical level.
All tests that make use of the F-distribution are collectively referred to as "F Tests." The F-Test to Compare Two Variances is often what is meant when the term "F-Test" is used. However, a number of tests, including regression analysis, the Chow test, and the Scheffe test, use the f-statistic. If we are conducting an F-Test, we might employ a variety of technological tools. since doing an F-test manually while accounting for variations is a difficult and time-consuming operation.
if the ratio of two sample variances exceeds the critical value of f at a defined confidence level, then the level of confidence also exceeds the critical level.
learn more about F-distribution,
https://brainly.com/question/13057442
#SPJ4
What is the value of a in this linear system?
a + b + c = 62
a - b = 12
2a + b + c = 92
O A.
14
OB.
30
OC.
18
o
c
D.
26
Answers
Answer:
Step-by-step explanation:
C
In AIJK, i = 25 inches, j = 46 inches and k=24 inches. Find the measure of ZJ to the nearest degree.
Answers
Answer:
140
Step-by-step explanation:
find the approximate area of the shaded region, given that the area of the sector is approximately 13.08 square units.

Answers
The area of the shaded region is 3915 units².
We have,
Area of the sector.
= 13.08 units²
Now,
To find the area of an isosceles triangle with side lengths 5, 5, and 4 units, we can use Heron's formula.
Area = √[s(s - a)(s - b)(s - c)]
where s is the semi-perimeter of the triangle, calculated as:
s = (a + b + c) / 2
In this case,
The side lengths are a = 5, b = 5, and c = 4. Let's calculate the area step by step:
Calculate the semi-perimeter:
s = (5 + 5 + 4) / 2 = 14 / 2 = 7 units
Use Heron's formula to find the area:
Area = √[7(7 - 5)(7 - 5)(7 - 4)]
= √[7(2)(2)(3)]
= √[84]
≈ 9.165 units (rounded to three decimal places)
Now,
Area of the shaded region.
= Area of the sector - Area of the isosceles triangle
= 13.08 - 9.165
= 3.915 units²
Thus,
The area of the shaded region is 3915 units².
Learn more about Circle here:
https://brainly.com/question/11833983
#SPJ1
Pls help it’s algebra 1

Answers
Answer:
Y+1=-1/2(x-4) the very bottom choice trust me its in point slope form and since the 1 is negative it turns into a positive for the equation and adds to the Y
Step-by-step explanation:
Jerome is a co-owner of a small company and received 1/3 of the company’s profits this year. What were the company’s overall profits if Jerome made $150,000? Type an equation and solve
Answers
Answer:
$450,000
Step-by-step explanation:
$150,000 times 3 because he made 1/3 of the profits
200 applicants applied to volunteer at an international tennis tournament.
14
of the applicants were successful. However, of the successful applicants, 15
couldn’t make all the training sessions and were discounted.
How many were selected to help at the tournament?
Answers
The number of volunteers who are selected for the tennis tournament is 40 as calculated by the fractions.
A fraction, which derives from the Latin word fractus, which means "broken," is a portion of a whole or, more broadly, any number of equal pieces. A fraction in spoken English refers to the number of components of a particular size.
A fraction consists of a numerator and a denominator. The numerator divided by the denominator is known as a fraction.
Compound fractions, complicated fractions, and mixed numeral fractions are examples of uncommon fractions that use numerators and denominators.
There are a total of 200 applicants who volunteered at the tennis tournament.
1/4 of the volunteers were successful.
Number of successful applicants= \(\frac{1}{4} \times 200=50\)
Now 1/5 of the successful candidates could not complete the training.
Number of unsuccessful candidates= \(\frac{1}{5} \times 50=10\)
Number of Volunteers selected to help at the tournament= 50-10=40
Hence 40 candidates were selected to help at the tournament.
Disclaimer: The complete correct question is :
200 applicants applied to volunteer at an international tennis tournament.1/4th of the applicants were successful. However, of the successful applicants, 1/5th couldn’t make all the training sessions and were discounted. How many were selected to help at the tournament?
To learn more about fractions visit:
https://brainly.com/question/10354322
#SPJ9
Choose all the numerals that when you multiplied by 58 equal a product greater than 58.
Answers
Carns Company is considering eliminating its Small Tools Division, which reported a loss for the prior year of $205,000 as shown below. Segment Income (Loss) Sales $ 1,430,000 Variable costs 1,295,000 Contribution margin 135,000 Fixed costs 340,000 Income (loss) $ (205,000) If the Small Tools Division is dropped, all of its variable costs are avoidable, and $119,000 of its fixed costs are avoidable. The impact on Carns’s income from eliminating the Small Tools Division would be: Multiple Choice
Answers
The impact on Carns Company's income from eliminating the Small Tools Division would be a decrease of $1,209,000.
To determine the impact on Carns Company's income from eliminating the Small Tools Division, we need to consider the avoidable costs associated with the division.
The avoidable costs include all of the variable costs of the division and a portion of the fixed costs that are specifically related to the Small Tools Division. In this case, the variable costs of the division are $1,295,000, and $119,000 of the fixed costs are avoidable.
To calculate the impact on income, we subtract the avoidable costs from the loss reported by the division:
Impact on income = Loss - Avoidable costs
Impact on income = $205,000 - ($1,295,000 + $119,000)
Impact on income = $205,000 - $1,414,000
Impact on income = -$1,209,000
The negative sign indicates a decrease in income.
For more such questions on income
https://brainly.com/question/28414951
#SPJ8
If a function f(x) is defined as 3x2 + x + 2, what is the value of Lim h-0 f(x+h)-f(x)/h? A. 3x + 1 B. 3x + 2 C. 6x + 1 D. 6x + 2
Answers
Answer:
\( f(x+h) = 3(x+h)^2 +(x+h) +2= 3(x^2 +2xh+h^2) +x+h+2\)
\(f(x+h) = 3x^2 +6xh +3h^2 +x+h+2= 3x^2 +6xh +x+h+ 3h^2 +2\)
And replacing we got:
\( lim_{h \to 0} \frac{3x^2 +6xh +x+h+ 3h^2 +2 -3x^2 -x-2}{h}\)
And if we simplfy we got:
\( lim_{h \to 0} \frac{6xh +h+ 3h^2 }{h} =lim_{h \to 0} 6x + 1 +3h \)
And replacing we got:
\(lim_{h \to 0} 6x + 1 +3h = 6x+1\)
And the bet option would be:
C. 6x + 1
Step-by-step explanation:
We have the following function given:
\( f(x) = 3x^2 +x+2\)
And we want to find this limit:
\( lim_{h \to 0} \frac{f(x+h) -f(x)}{h}\)
We can begin finding:
\( f(x+h) = 3(x+h)^2 +(x+h) +2= 3(x^2 +2xh+h^2) +x+h+2\)
\(f(x+h) = 3x^2 +6xh +3h^2 +x+h+2= 3x^2 +6xh +x+h+ 3h^2 +2\)
And replacing we got:
\( lim_{h \to 0} \frac{3x^2 +6xh +x+h+ 3h^2 +2 -3x^2 -x-2}{h}\)
And if we simplfy we got:
\( lim_{h \to 0} \frac{6xh +h+ 3h^2 }{h} =lim_{h \to 0} 6x + 1 +3h \)
And replacing we got:
\(lim_{h \to 0} 6x + 1 +3h = 6x+1\)
And the bet option would be:
C. 6x + 1
Answer:
6x+1
Step-by-step explanation:
Plato :)
A line passes through -8,5 and has a slope of 3/4 write the equation in slope intercept form
Answers
The equation of the line in slope-intercept form is y = (3/4)x.
To write the equation of a line in slope-intercept form, we need to use the slope-intercept form equation: y = mx + b,
where m is the slope and b is the y-intercept.
Given that the line passes through the point (-8, 5) and has a slope of 3/4, we can substitute the values into the equation to find the y-intercept (b).
First, let's find the value of b using the point-slope form equation: y - y1 = m(x - x1), where (x1, y1) is a point on the line.
Using (-8, 5) as the point and 3/4 as the slope, we have:
5 - 5 = (3/4)(-8 - x)
0 = (3/4)(-8 - x)
0 = (-3/4)(8 + x)
0 = -6 - (3/4)x
Next, we can solve for x:
(3/4)x = -6
x = -6 \(\times\) (4/3)
x = -8
Now that we have the value of x, we can substitute it back into the equation to find the value of b:
0 = -6 - (3/4)(-8)
0 = -6 + 6
0 = 0
So, the value of b is 0.
Finally, we can write the equation of the line in slope-intercept form:
y = (3/4)x + 0
y = (3/4)x.
For similar question on slope-intercept form.
https://brainly.com/question/1884491
#SPJ8
A
B
C
D
37. What is the length of side P in the figure below?
6.7 cm
11 cm
15 cm
45 cm
20 cm
25 cm
P

Answers
The length of the side P is 15 cm. And the right option is C.
What is Pythagoras theorem?Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides.
To calculate the length of side P we use Pythagoras theorem's formula
Pythagoras formula:
a² = b²+c²......................... Equation 1Where:
a = Diagonal of the rectangleb = Length of the rectanglec = Width of the rectangleFrom the diagram,
Given:
a = 25 cmb = 20 cmc = p cmSubstitute these values into equation 1
25² = 20²+p²p² = 25²-20²p² = 225p = √225p = 15 cmHence, the right option is C 15 cm.
Learn more about Pythagoras theorem here: https://brainly.com/question/27997683
#SPJ1
Find the original slope of (-6,-1) and (0,3)
Answers
Answer:
slope (m) = 2/3
Step-by-step explanation:
slope = change in x /change in y
Also, slope is y2 - y1 / x2 -x1. That is what I apply for this activity, hence:
slope = 3 - (-1) / 0 - (-6)
= 3 + 1 / 0 + 6
= 4 / 6
= 2/3
∴ slope(m) = 2/3
Hi can someone please help me solve the following system of inequalities and state the coordinates in the solution setz

Answers
The graph of the system of the inequalities is attached.
To graph the inequalities y < -x - 4 and y ≥ (3/5)x + 4, we can start by graphing the corresponding equations and then shade the appropriate regions based on the inequality signs.
Let's begin with the equation y = -x - 4:
Choose a range of x-values to plot.
For simplicity, let's use x-values from -10 to 10.
Substitute different x-values into the equation to find corresponding y-values.
For example:
When x = -10, y = -(-10) - 4 = 10 - 4 = 6.
When x = 0, y = -(0) - 4 = -4.
When x = 10, y = -(10) - 4 = -10 - 4 = -14.
Plot these points on the coordinate plane and draw a straight line passing through them.
This line represents the equation y = -x - 4.
Next, let's graph the equation y = (3/5)x + 4:
Again, choose a range of x-values to plot. Let's use the same range of -10 to 10.
Substitute different x-values into the equation to find corresponding y-values. For example:
When x = -10, y = (3/5)(-10) + 4 = -6 + 4 = -2.
When x = 0, y = (3/5)(0) + 4 = 0 + 4 = 4.
When x = 10, y = (3/5)(10) + 4 = 6 + 4 = 10.
Plot these points on the coordinate plane and draw a straight line passing through them.
This line represents the equation y = (3/5)x + 4.
Now, let's shade the regions based on the inequalities:
For y < -x - 4, we need to shade the region below the line y = -x - 4.
For y ≥ (3/5)x + 4, we need to shade the region above or on the line y = (3/5)x + 4.
Hence, the region where the shaded regions overlap represents the solution to both inequalities.
Learn more about system of inequalities click;
https://brainly.com/question/29785389
#SPJ1

solve help
3+ x + 4 =
Answers
Answer:
7+x
Step-by-step explanation:
Add 3 and 4
3+4= 7
You can't add x since it's a variable so you just leave it as it is.
Hope this helps!
Noah bought 2.5 kilograms of colored tiles chips for a mosaic art project. What is the mass of the tile chips in grams?_____________________
Answers
Answer:
2500 grams
Step-by-step explanation:
This exercise refers to choosing two cards from a shuffled deck. Assume that the deck is shuffled after a card is returned to the deck. If you put the first card back in the deck before you draw the next, what is the probability that the first card is a club and the second is a diamond?
(Enter your answer as a fraction)
Answers
The probability that the first card is a club and the second is a diamond, given that the deck is shuffled after each draw and the first card is replaced before the second draw, is 1/208.
What is Probability?It is a branch of mathematics that deals with the occurrence of a random event.
If the deck is shuffled after a card is returned, then the probability of drawing any particular card on the first draw is 1/52, since there are 52 cards in the deck and each card is equally likely to be drawn.
Assuming the first card drawn is a club, there are 13 clubs remaining in the deck out of 52 cards, so the probability of drawing a diamond on the second draw is 13/52.
The probability of drawing a club followed by a diamond
P(club followed by diamond) = P(club on first draw) x P(diamond on second draw given club on first draw)
= (13/52) x (1/52)
= 1/208
Therefore, the probability that the first card is a club and the second is a diamond, given that the deck is shuffled after each draw and the first card is replaced before the second draw, is 1/208.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ1
Find the mean of the data summarized in the given frequency distribution. Compare the computed mean to the actual mean of 56.6 degrees. Low Temperature (◦F) 40−44 45−49 50−54 55−59 60−64 Frequency 2 7 9 5 2 The mean of the frequency distribution is nothing degrees.
Answers
Answer:
Computed mean = 51.6
Actual mean > computed mean
Step-by-step explanation:
Low temp. - - Freq(f) - - midpoint(x) - - fx
40−44 - - - - - 2 - - - - - - - 42 - - - - - - 84
45−49 - - - - - 7 - - - - - - - 47 - - - - - - 329
50−54 - - - - - 9 - - - - - - - 52 - - - - - - 468
55−59 - - - - - 5 - - - - - - - 57 - - - - - - 285
60−64 - - - - - 2 - - - - - - - 62 - - - - - - 124
Mean (m) = Σ(fx) / Σ(f)
Σ(fx) = 84 + 329 + 468 + 285 + 124 = 1290
Σ(f) = 2 + 7 + 9 + 5 + 2 = 25
Mean (m) = 1290 / 25
Computed mean (m) = 51.6
Actual mean = 56.6
Actual mean > computed mean
56.6 > 51.6
In 1999. Sara and her brother Xzavier got money when their rich uncle died. They
each got the same amount of money. Sara bought some land in the country
because she heard they would be building houses near there some day. She
bought 300 acres of land with all of the money she got from her uncle,
$600,000, in 2000. In 2003 they extended the main highway to go near her land
and she sold 100 acres for $2700 lacre. In 2005 she sold half of the land she had
left for $3600 lacre. In 2007 they started a long-term project to build houses in
the area and built a Lowes, a Food Lion, A Bank of America and a Burger King on
the main street. Finally, in 2010. Sara sold the rest of her land for $400,000. What
was her total profit when she finished selling all of the land?
Answers
Answer:
$406,300
Step-by-step explanation:
$2,700 + $3,600 = $6,300
$400,000 + $6,300 = $406,300
what is inequalities
Answers
Inequalities are used in various branches of mathematics, as well as in real-world applications such as economics, physics, and social sciences, to describe relationships, make comparisons, and analyze data.
Inequalities are mathematical statements that describe a relationship between two values or expressions, indicating that one is greater than, less than, or not equal to the other. Inequalities are used to compare quantities and express their relative sizes or order.
The most common symbols used in inequalities are:
">" (greater than): indicates that the value on the left side is larger than the value on the right side.
"<" (less than): indicates that the value on the left side is smaller than the value on the right side.
"≥" (greater than or equal to): indicates that the value on the left side is greater than or equal to the value on the right side.
"≤" (less than or equal to): indicates that the value on the left side is less than or equal to the value on the right side.
"≠" (not equal to): indicates that the values on both sides are not equal.
Inequalities can be represented using variables, constants, and mathematical operations such as addition, subtraction, multiplication, and division. Solutions to inequalities are often expressed as intervals or sets of values that satisfy the given inequality.
Inequalities are used in various branches of mathematics, as well as in real-world applications such as economics, physics, and social sciences, to describe relationships, make comparisons, and analyze data.
For more questions on inequalities
https://brainly.com/question/25275758
#SPJ8
Please see screenshot.

Answers
Answer:
See below
Step-by-step explanation:

Write a proportion: At a candy store, it costs $0.25 to buy 5
inches of rope candy. Write an equation to find x, the length
of rope candy that can be bought for $1.80?
Answers
Answer:
The proportion is:
$0.25 / 5$ inches $= x / $ inches bought for $1.80
Simplifying the left-hand side:
$0.25 / 5 = 0.05$
The equation to find x becomes:
$0.05 = x / 1.80$
To solve for x, we can multiply both sides by 1.80:
$0.05 \cdot 1.80 = x$
$x = 0.09$
Therefore, the length of rope candy that can be bought for $1.80 is 0.09 inches.
Answer: 36
Step-by-step explanation:
.25/5 = .05
1.80/.05 = 36
Jimmy runs 16 laps around the track every day. If he decides to run 24 laps today. what percent of the laps did he run?
Answers
Answer:
150%
Step-by-step explanation:
Answer:
66.7%
Step-by-step explanation:
\( \frac{16}{24} \times 100 = 66.67\)
Can somebody explain how I do this?

Answers
Answer:
You carry the 1 bring the 2 then divide by 3 multiply by 4 times the 2nd power then gimme those points.
Step-by-step explanation:
i have no vlue
Each week as part of her workout, Monica walks 0.5 mile, runs 1.6 miles, and then walks 0.75 mile.
How many total miles will Monica walk and run in a year? Reminder: there are 52 weeks in a year.
Enter your answer in the box.
miles
Answers
Answer:
-2 or -5
Step-by-step explanation:
( shown in photo below )

A parabola can be represented by the equation y2=12x which equation represents directrix?
Answers
Answer:
x=-3
Step-by-step explanation:
The equation of the directrix is x = -3
Given the general equation of a parabola expressed as
(y-y0)² = 4a(x-x0) ... 1
Equation of the directrix will be expressed as x = x0 - a
From the equation given;
y² = 12x ... 2
Comparing 1 and 2;
x - x0 = x
-x0 = x - x
-x0 = 0
x0 = 0
Similarly;
y-y0 = y
-y0 = y - y
-y0 = 0
y0 = 0
Also;
4a = 12
a = 12/4
a = 3
Substituting x0 =0, y0 = 0 and a = 3 into the equation of the dirrectrix above, we will have;
x = x0 - a
x = 0 - 3
x = -3
Hence the equation of the directrix is x = -3
Learn more at https://brainly.com/question/18707630

DF bisects EDG. Find FG. The diagram is not to scale.

Answers
n + 5 = 2n - 6
n - 2n = -6 - 5
-n = -11
n = -11/-1
n = 11
FG = 2n - 6
FG = 2(11) - 6
FG = 22 - 6
FG = 16
Since the mode is the most frequently occurring data value, it
Select one:
a. is always larger than the mean
b. can never be larger than the mean
c. must have a value of at least two
d. is always larger than the median
e. None of these answers is correct.
Any answer without justification will be rejected automatically.
Answers
The correct answer is option (e): None of these answers is correct.
The statement "the mode is the most frequently occurring data value" is true. However, none of the options provided accurately describes the relationship between the mode and the mean.
The mode and the mean are different measures of central tendency and can have different values. There is no general rule or guarantee that the mode will always be larger or smaller than the mean. The relationship between the mode and the mean depends on the specific dataset and its distribution. Therefore, none of the provided options correctly describes the relationship between the mode and the mean.
Evaluate the function when x= -2,0, and 5 h(x)= -2x+9
Answers
Given:
a function is given as h(x) = -2x + 9
Find:
we have to evaluate the function at x = -2 , 0 and 5.
Explanation:
when x = -2
h(-2) = -2(-2) + 9 = 4 + 9 = 13
when x = 0
h(0) = -2(0) + 9 = 0 + 9 = 9
when x = 5
h(5) = -2(5) + 9 = - 10 + 9 = -1
Therefore, the values of given function h(x) are 13, 9 , -1 at x = -2, 0 , 5 respectively.
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8